Тема 5. Введение в анализ

Основные теоретические сведения

1. Пусть даны два непустых множества X и Y. Если каждому элементу x из множества Х по определенному правилу ставится в соответствие один и только один элемент у из Y, то говорят, то говорят, что на множестве Х задана функция (или отображение) со множеством значений Y. Это можно записать так: 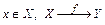или , где множество Х называется областью определения функции, а множество Y, состоящее из всех чисел вида 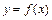, 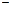множеством значений функции.

2. К основным элементарным функциям относятся:

1) степенная функция y= 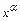, где ;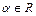

2) показательная функция y=a^x, где ;

3) логарифмическая функция y= , где ;

4) тригонометрические функции: , ;

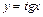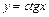5) обратные тригонометрические функции: y =arccos x, y =arctg x, y =arcctg x.

3. Число А называется пределом функции f (x) при 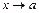, если для любого 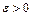найдется 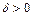такое, что 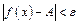при

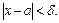
Это записывают так: .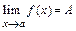

Практическое вычисление пределов основывается на следующих свойствах.

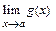Если существуют и , то

1) ;

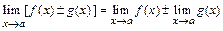2) ;

3) 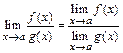(при )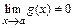

4. Функция f (x) (F (x)) называется бесконечно малой (бесконечно большой) при 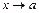, если .

5. Нарушение ограничений, накладываемых на функции при вычислении их пределов, приводят к неопределенностям вида 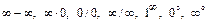. Элементарными приемами раскрытия неопределенностей являются: 1) сокращение на множитель, создающий неопределенность; 2) деление числителя и знаменателя на старшую степень аргумента (для отношения многочленов при ); 3) использование двух замечательных пределов:

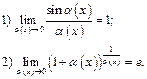
Отметим также, что

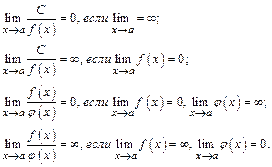
Пример 1. Найти

Решение. Подставляя вместо x его предельное значение, равное 3, получаем в числителе бесконечно большую, а в знаменателе – бесконечно малую функцию:

Поэтому

Пример 2. Найти .

Решение. Подстановка предельного значения аргумента приводит к неопределенности вида 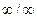. Так как под знаком предела стоит отношение двух многочленов, то разделим числитель и знаменатель на старшую степень аргумента, т.е. на x ⁴. В результате получим

поскольку при функции 5/ x ³ и 7/ x ⁴ являются бесконечно малыми.

Пример3. Найти

Решение. Подстановка x = 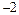приводит к неопределенности 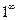. Произведем замену переменных: Тогда

Здесь использован второй замечательный предел.

Дата добавления: 2014-11-16