Канонические уравнения

Аналитическая геометрия в пространстве.

1. Общее уравнение плоскости имеет вид 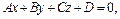где нормальной вектор плоскости (рис. 6).

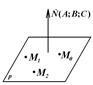
Рис.6

Уравнение плоскости, проходящей через три заданные точки и 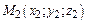имеет вид:

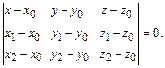(6)

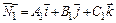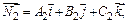2. Угол между двумя плоскостями, имеющими нормальные векторы и определяется как угол между и 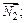косинус этого угла находится по формуле

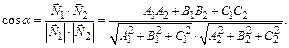(7)

3. Расстояние от точки до плоскости, определяемой уравнением 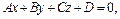находится по формуле

(8)

4. Уравнение плоскости, проходящей через точку и перпендикулярной вектору , имеет вид

(9)

5. Уравнения прямой в пространстве, проходящей через две заданные точки и 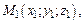имеют вид:

(10)

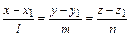(11)

определяют прямую, проходящую через точку и параллельно вектору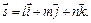

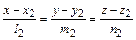6. Угол между двумя прямыми, заданными их каноническими уравнениями и , определяется по формуле

. (12)

7. Угол между прямой 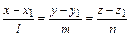и плоскостью 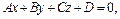определяется по формуле

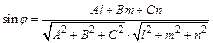. (13)

Пример 3. Даны координаты вершин пирамиды 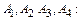Составить уравнение прямой, проходящей через 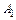и ; составить уравнения плоскостей и 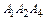; найти угол между ребром 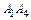и гранью ; найти угол между плоскостями и 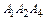; найти расстояние от точки до плоскости ; составить уравнение плоскости, проходящей через вершину параллельно плоскости .

Решение. 1. Подставив координаты вершин 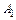и в формулу (10), получим уравнение прямой

().

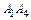2. Уравнение плоскости получим, подставив координаты вершин в формулу (6):

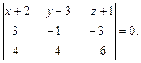
Вычислим определитель разложением по элементам 1-ой строки

(х +2)

т.е.

Аналогично получаем уравнение плоскости : .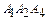

3. Угол между ребром 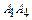и гранью найдем по формуле (13), подставив , .

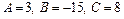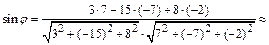0,63,

откуда 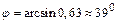=0,68 рад.

4. По уравнениям плоскостей и 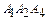определяем их нормальные векторы: , . Угол между плоскостями находим по формуле (7):

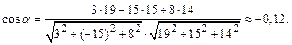
Отсюда следует, что 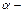тупой угол, равный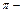 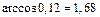рад с точностью до 0,01. Это и есть искомый угол между плоскостями и .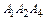

5. Расстояние от точки (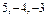) до плоскости найдем по формуле (8):

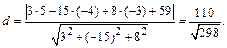
6. Уравнение плоскости, проходящей через вершину (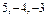) параллельно плоскости с нормальным вектором , получим по формуле (9):

т.е.

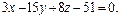
Дата добавления: 2014-11-16