Тема 4. Комплексные числа

Основные теоретические сведения.

1. Выражение вида z=x+yi= 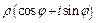называется комплексным числом (в алгебраической и тригонометрической форме соответственно). Здесь 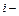мнимая единица, x =Re z действительная часть, а y =Im z –мнимая часть комплексного числа z; 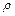и 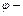модуль и аргумент числа z:

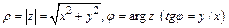. (1)

Комплексные числа изображаются точками на комплексной плоскости (рис.7).

рис.7

2. Арифметические действия над комплексными числами.

Два комплексных числа 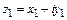и 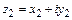называются равными, если равны их действительные и мнимые части, т.е. 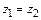, если , .

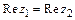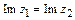Сложение (вычитание) комплексных чисел:

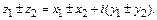(2)

Умножение комплексных чисел:

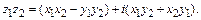(3)

В частности,

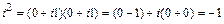, т.е. мнимая единица есть число, квадрат которого равен .

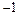Деление двух комплексных чисел

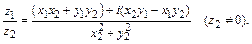(4)

3. Извлечение корня n-й степени (n–натуральное число) из числа 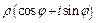z= (z 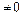)производится по формуле

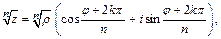(5)

где 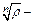арифметический корень из модуля z, a k =0,1, …, n 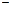1.

Пример 1. Найти полярные координаты точки М (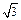; 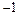) (рис.8).

x

M  

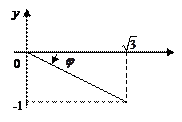
рис. 8

Решение. Используя формулы (1), находим полярный радиус и полярный угол точки М: 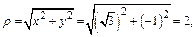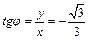, , 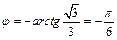т.к. точка М лежит в IV четверти.

Пример 2. Даны комплексные числа 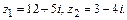Найти , , .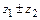

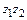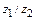Решение.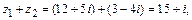

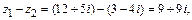
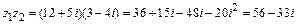(учли, что ).

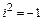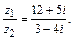Умножая числитель и знаменатель на сопряженное делителю комплексное число 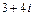, получим

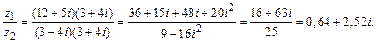
Пример 3. Изобразить на комплексной плоскости числа:1) ,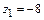

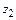2) =2 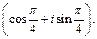Записать число z₁ в тригонометрической, а число z ₂ 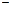в алгебраической форме.

Решение. 1) Для числа z ₁ имеем x ₁=Re z ₁= 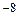, y ₁=Im z ₁=0. Откладывая по оси Оx x ₁= 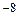, а по оси Оy 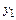=0, получаем точку комплексной плоскости, соответствующую числу z ₁ (рис.9).

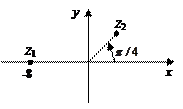
Рис.9

Модуль этого числа находим по формуле (1): 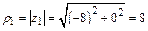. Аргумент определяем из равенства 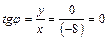. Так как число z₁ находится в левой полуплоскости, то его аргумент .

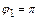Тригонометрическая форма числа z ₁ имеет вид z ₁=8 .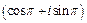

2) Модуль числа z ₂ равен 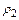, а аргумент 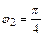. Для его изображения на комплексной плоскости проводим из полюса луч под углом 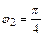к полярной оси и откладываем на нем отрезок длиной 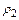=2. Полученная точка соответствует числу z ₂ (рис.9). Его действительная часть 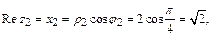а мнимая часть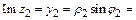 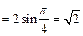. Таким образом, алгебраическая форма числа z₂ имеет вид: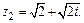

Пример 4. Вычислить .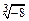

Решение. Модуль числа 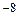равен 8, а аргумент равен 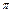. Используя формулу (2), получаем

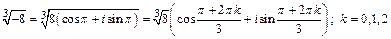
При k =0:

При k =1:

.

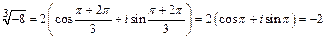При k =2:

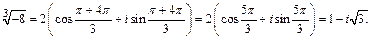
Дата добавления: 2014-11-16