Кривых, заданных общим уравнением

Преобразование координат на плоскости. Построение

Парабола

Параболой называется множество точек, равноудаленных от некоторой точки, называемой фокусом, и прямой, называемой директрисой.

Пусть точка F –фокус параболы, а прямая l –ee директриса и задано расстояние между ними, равное p. В системе координат x0y, где ось 0x проходит через фокус F перпендикулярно директрисе l, а начало координат выбрано посередине между ними, уравнение параболы имеет вид

p >0.

Парабола не имеет асимптот. Эксцентриситет параболы равен 1 и не влияет на форму кривой. Вид кривой показан на рис.4.

Рис.4

Если сравнить канонические уравнения эллипса, окружности, гиперболы и параболы с общим уравнением кривой второго порядка (1), то видно, что в них коэффициенты B=D=E =0. Если в этом уравнени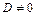и , или то чтобы привести уравнение к каноническому виду, определить тип кривой и построить ее, необходимо сделать преобразование координат.

Если в уравнении (5) 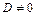или , то центр симметрии эллипса или гиперболы, или центр окружности, или вершина параболы находятся не в начале координат, а в некоторой точке Строить кривую в данном случае удобно, перенеся начало координат в эту точку, то есть сделав замену

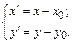
При такой замене в новой системе координат с началом в точке и осями и уравнение кривой будет иметь канонический вид.

Приведем уравнения различных прямых:

1. Уравнение эллипса с центром симметрии в точке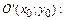

2. Уравнение гиперболы с центром симметрии в точке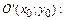

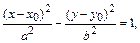
здесь вершины в точках (а; 0) и (; 0);

здесь вершины в точках (0; b) и (0; ).

3. Уравнение параболы с вершиной в точке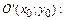

ось симметрии параллельна Оx;

ось симметрии параллельна .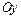

Знак 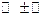показывает направление ветвей параболы. Если в уравнении знак , то направление ветвей совпадает с направлением оси, которой параллельна ось симметрии параболы, а если , то направление ветвей противоположно направлению оси, которой параллельна ось симметрии параболы.

Пример 1. Даны вершины треугольника ABC: А (;8), B (5; ), C (10;6). Найти: 1) длину стороны AB; 2) уравнения сторон AB и AC и их угловые коэффициенты; 3) внутренний угол А в радианах с точностью до 0,01; 4) уравнение высоты CD и ее длину.

Решение: 1. Подставив в формулу (1) координаты точек А и В, имеем:

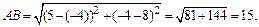
2. Подставив координаты точек А и В в формулу (2), получим уравнение прямой АВ:

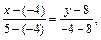
3 y = x , 4 x +3 y 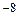=0 (AB).

Для нахождения углового коэффициента прямой АВ разрешим полученное уравнение относительно y: y = 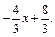Отсюда = 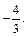Найдем уравнение прямой АС:

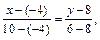
х +7 y –5 =0 (AC).

Отсюда =

3. Угол А, образованный прямыми АВ и АС, найдем по формуле (3), подставив в нее = =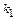

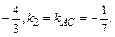
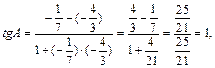
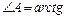1= рад.

4. Так как высота CD перпендикулярна стороне АВ, то угловые коэффициенты этих прямых обратны по величине и противоположны по знаку, т.е.

Уравнение прямой, проходящей через данную точку 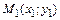в заданном угловым коэффициентом k направлении, имеет вид:

Подставив координаты точки С и 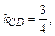получим уравнение высоты CD:

(CD).

Для нахождения длины CD определим координаты точки D, решив систему уравнений (АВ) и (CD):

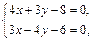
откуда x =2, y =0, то есть D (2;0).

Подставив в формулу (1) координаты точек С и D, находим:

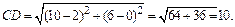
Пример 2. Построить кривую, заданную уравнением 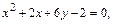приведя его к каноническому виду.

Решение. Преобразуем уравнение следующим образом:

;

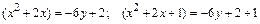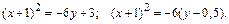
Получим уравнение параболы с вершиной в точке и осью симметрии, параллельной оси 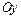. Перенеся начало координат в точку , получим в системе координат уравнение

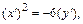
где параметр р определяется из условия 2 р =6, или р =3.

Парабола симметрична относительно оси или относительно прямой x = .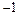

Фокус параболы находится на ее оси и отстоит от вершины на Поскольку из уравнения следует, что 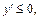то ветви параболы направлены вниз и фокус F лежит на 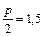ниже вершины, то есть его координаты .

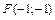Директрисой параболы является прямая, перпендикулярная ее оси и находящаяся на расстоянии 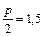от вершины, причем фокус и директриса расположены по разные стороны от вершины. Учитывая все это, можно записать уравнение директрисы y =0,5+1,5, или y =2. Кривая приведена на рис.5.

Рис.5

Если в уравнении (5) то оси симметрии кривой не параллельны координатным осям. Чтобы получить каноническое уравнение кривой, необходимо повернуть систему координат.

Дата добавления: 2014-11-16