
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 2. Элементы векторной алгебры
|
|
|
|
Основные теоретические сведения.
1. Скалярным произведением двух векторов  и
и 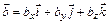 называется число, определяемое равенством
называется число, определяемое равенством
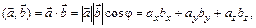 (1)
(1)
где 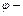 угол между векторами
угол между векторами 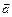 и
и 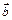 .
.
2. Косинус угла  между векторами
между векторами  и
и 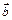 вычисляется по формуле
вычисляется по формуле
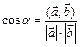 (2)
(2)
3. Векторным произведением двух векторов 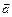 и
и 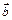 называется вектор
называется вектор  , длина которого равна произведению длин векторов-сомножителей на синус угла между ними и который направлен перпендикулярно векторам
, длина которого равна произведению длин векторов-сомножителей на синус угла между ними и который направлен перпендикулярно векторам 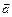 и
и 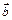 так, что векторы
так, что векторы 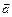 ,
, 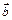 ,
,  образуют правую тройку (рис. 1):
образуют правую тройку (рис. 1):

Рис.1

 (3)
(3)
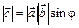 .
.
Геометрически 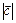 равен площади
равен площади  параллелограмма, построенного на векторах
параллелограмма, построенного на векторах 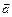 и
и 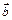 :
:
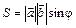 .
.
4. Смешанное произведение трех векторов  ,
, 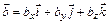 ,
, 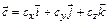 есть число, равное
есть число, равное
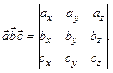
 (4)
(4)
Модуль смешанного произведения равен объему параллелепипеда, построенного на векторах 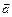 ,
, 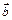 ,
,  .
.
Пример 1. По координатам вершин пирамиды
 найти: 1) длины ребер
найти: 1) длины ребер 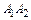 и
и  2) угол между ребрами
2) угол между ребрами 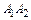 и
и  3) площадь грани
3) площадь грани  4) объем пирамиды
4) объем пирамиды 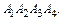
Решение. 1)Находим векторы 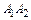 и
и 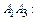


Длины этих векторов, т. е. длины ребер 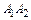 и
и 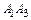 , таковы:
, таковы:
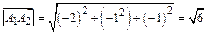 ;
;
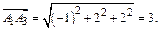
2) Скалярное произведение векторов 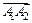 и
и  находим по формуле (1):
находим по формуле (1):

а косинус угла между ними–по формуле (2):
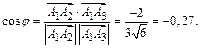
Отсюда следует, что 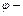 тупой угол, равный
тупой угол, равный 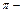
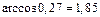 рад с точностью до 0,01. Это и есть искомый угол между ребрами
рад с точностью до 0,01. Это и есть искомый угол между ребрами 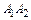 и
и 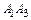 .
.
3) Площадь грани  равна половине параллелограмма, построенного на векторах
равна половине параллелограмма, построенного на векторах 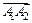 и
и  , т. е. половине модуля векторного произведения этих векторов [см. формулу (2)]:
, т. е. половине модуля векторного произведения этих векторов [см. формулу (2)]:
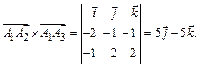
Здесь определить вычисляется с помощью разложения по первой строке. Cледовательно,
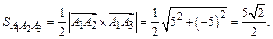
4) Объем  пирамиды равен
пирамиды равен  объема параллелепипеда, построенного на векторах
объема параллелепипеда, построенного на векторах  Вектор
Вектор  Используя формулу (4), получаем
Используя формулу (4), получаем

|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 365; Нарушение авторских прав?; Мы поможем в написании вашей работы!