Характеристика вагонов 81-717(714) 4 страница

В настоящее время обратный осмос начали применять как один из наи«более экономичных способов опреснения воды. Солевой раствор (например, морскую воду) отделяют полупроницаемой мембраной от пресной воды и под-вергаюг давлению белее высокому, чем осмотическое давление раствора. В ре-зультате часть содержащейся в растворе воды «вытесняется» в фазу пресной воды, а концентрация солен в оставшемся растворе повышается. Концентриро-ванный солевой раствор периодически заменяют свежими порциями подлежа" щей опреснению воды.

79. Давление пара растворов. При данной температуре давле­ние насыщенного пара над каждой жидкостью — величина посто­янная. Опыт показывает, что при растворении в жидкости какого-либо вещества давление насыщенного пара этой жидкости пони-, жается. Таким образом, давление насыщенного пара растворителя над раствором всегда ниже, чем, над чистым растворителем при той же температуре. Разность между этими величинами принято называть понижением давления пара над раствором (или понижением давления пара раствора). Отношение величины этого понижения к давлению насыщенного пара над чистым раствори*, телем называется относительным понижением давлен н и я пара над раствором.

Обозначим давление насыщенного пара растворителя над' чи«; стым растворителем через р₀, а над раствором через р. Тогда отно­сительное понижение давления пара над раствором будет пред­ставлять собою дробь:

(Ро — Р)/Ро

В 1887 г. французский физик Рауль, изучая растворы различ­ных нелетучих * жидкостей и веществ в твердом состоянии, уста­новил закон, связывающий понижение давления пара над разбав­ленными растворами неэлектролитов с концентрацией:

Относительное понижение давления насыщенного пара растворителя над раствором равно молярной доле раство­ренного вещества.

Математическим выражением закона Рауля является уравне-* ние:

(.Ро — Р)/Ро = Ni

* В случае растворов летучих веществ закономерности носят более слож­ный характер, поскольку над раствором находится смесь паров растворенного вещества и растворителя.

Здесь N₂ — молярная доля растворенного вещества. Явление понижения давления насыщенного пара над раствором вытекает из принципа Ле Шателье. Представим себе равновесие

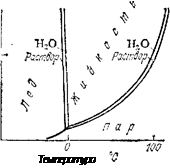Рис. 73. Диаграмма состояния воды и водно­го раствора нелетучего вещества.

между жидкостью, например, во­дой, и ее паром. Это равновесие, которому отвечает определенное давление насыщенного пара, можно выразить уравнением

(Н₂0)_жидк —^ (Н₂0)_пар

Если теперь растворить в во­де некоторое количество какого-либо вещества, то концентрация молекул воды в жидкости понизится и пойдет процесс, увеличи­вающий ее, — конденсация пара. Новое равновесие установится при более низком давлении насыщенного пара.

Понижение давления пара над раствором находит отражение на диаграмме состояния. На рис. 78 приведена схема диаграммы состояния воды и водного раствора нелетучего вещества. Согласно закону Рауля, давление водяного пара над водным раствором ниже, чем над водой. Поэтому кривая кипения для раствора лежит ниже, чем для воды. При переходе от воды к раствору изменяется также положение кривой плавления. И кривая кипения, и кривая плавления раствора расположены тем дальше от соответствующих кривых воды, чем концентрированнее раствор.

80. Замерзание и кипение растворов. Индивидуальные веще­ства характеризуются строго определенными температурами пере­ходов из одного агрегатного состояния в другое (температура ки­пения, температура плавления или кристаллизации). Так, вода при нормальном атмосферном давлении (101,3 кПа) кристалли­зуется при температуре 0 °С и кипит при 100 °С.

Иначе обстоит дело с растворами. Присутствие растворенного вещества повышает температуру кипения и понижает температуру замерзания растворителя, и тем сильнее, чем концентрированнее раствор. В большинстве случаев из раствора кристаллизуется (при замерзании) или выкипает (при кипении) только растворитель вследствие чего концентрация раствора в ходе его замерзания или кипения возрастает. Это, в свою очередь, приводит к еще боль­шему повышению температуры кипения и снижению температуры замерзания. Таким образом, раствор кристаллизуется и кипит не при определенной температуре, а в некотором температурном ин­тервале. Температуру начала кристаллизации и начала кипения данного раствора называют его температурой кристаллизации и температурой кипения.

Разность между температурами кипения раствора и чистого растворителя называют повышением температуры кипе­ния раствора (Лг_К1Ш). Разность между температурами замер­зания чистого растворителя и раствора называют понижением

температуры замерзания раствора (А/зам). Обозна-

чая температуры кипения и замерзания раствора

и /₃

а те

же величины для чистого растворителя г_КИп и /_зан, имеем:

^кип — ^кнп 'кип'

^Д'зам = *заы ^— '

Всякая жидкость начинает кипеть при той температуре, при ко­торой давление ее насыщенного пара достигает величины внеш­него давления. Например, вода под давлением 101,3 кПа кипит прн 100°С потому, что при этой температуре давление водяного пара как раз равно 101,3 кПа. Если же растворить в воде какое-нибудь нелетучее вещество, то давление ее пара понизится. Чтобы довести давление пара полученного раствора до 101,3 кПа, нужно нагреть раствор выше 100 °С. Отсюда следует, что температура ки­пения раствора всегда выше температуры кипения чистого раство­рителя. Аналогично объясняется и понижение температуры замер­зания растворов.

Повышение температуры кипения и понижение температуры замерзания растворов соответствуют принципу Ле Шателье. Рас­смотрим в этом плане замерзание раствора. Пусть имеется равно­весие между жидкостью н твердой фазой, например, равновесие вода — лед при 0 °С. Его можно выразить уравнением:

(Н₂0)_то ^=fc (Н₂0)_жпдк

Если растворить в воде некоторое количество какого-либо ве­щества, то концентрация молекул воды в жидкости понизится и пойдет процесс, увеличивающий ее, — плавление льда. Для уста­новления нового равновесия необходимо понизить температуру.

Повышение температуры кипения и понижение температуры за­мерзания находят отражение на диаграмме состояния. На рис. 79 приведена часть диаграммы состояния воды и раствора — отрез­ки кривых плавления и кипения в области давлений, близких

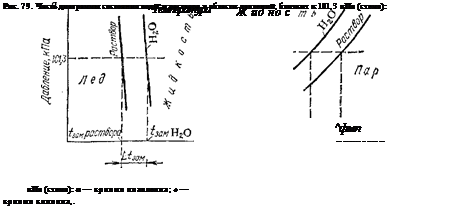
к нормальному атмосферному давлению (101,3 кПа). Отрезки пере­сечены горизонталью, отвечающей давлению 101,3 кПа (масштаб чертежа увеличен по сравнению с рис. 73 и 78). Видно, что точки пересечения этой горизонтали с.кривыми плавления и кипения для воды и для раствора различны. Абсциссы этих точек — темпера­тура замерзания и температура кипения — для воды равны 0 н 100 °С, а для раствора они соответственно ниже 0 °С и выше 100 °С. Кривые, отвечающие раствору, тем больше удалены от соответ­ствующих кривых воды, чем концентрированнее раствор. Поэтому и разность между температурами кипения или замерзания воды и раствора тем больше, чем выше концентрация раствора.

Изучая замерзание и кипение растворов, Рауль установил, что для разбавленных растворов неэлектролитов повышение темпера­туры кипения и понижение температуры замерзания пропорцио­нальны концентрации раствора:

Дгкип = Ет; Дг_зам = Km

Здесь т — молярная концентрация (моляльность); Е и К — эбуллиоскопическая* и криоскопическая** постоянные, зависящие только от природы растворителя, но не за­висящие от природы растворенного вещества. Для воды криоско­пическая постоянная К равна 1,86, эбуллиоскопическая постоян­ная Е равна 0,52. Для бензола К = 5,07, Е — 2,6.

На измерениях температур кипения и замерзания растворов основаны эбуллиоскопический и криоскопический методы определения молекулярных масс веществ. Оба метода широко используются в химии, так как, применяя различные рас­творители, можно определять молекулярные массы разнообразных веществ.

Пример. При растворении 2,76 г глицерина в 200 г воды температура за­мерзания понизилась на 0,279 градусов. Определить молекулярную массу гли­церина.

Находим, сколько граммов глицерина приходится в растворе на 1000 г воды:

р = 2,76- 1000/200 = 13,8 г

Выражаем моляльность раствора (т) через массу глицерина (р), приходя­щуюся на 1000 г воды, и его молярную массу (Л1);

т = _Р[М = 13,8/М

Подставляем данные в уравнение:

Дг_зам = Km; 0,279 = 1,86 • 13,8/М

* От лат. «ebuliire» — выкипать. ^:* От греч, «криос» — холод.

Отсюда молярная масса глицерина М — 92 г/моль, а молекулярная масса равна 92.

Глава РАСТьОРЫ ЭЛЕКТРОЛИТОВ

VIII

81. Особенности растворов солей, кислот и оснований. В гла­ве VII мы познакомились с законами, которым подчиняются раз­бавленные растворы. Справедливость этих законов подтверждается результатами многих экспериментов. Однако имеются вещества, растворы которых сильно отклоняются от всех рассмотренных за­конов. К подобным веществам относятся соли, кислоты и щелочи. Для них осмотическое давление, понижение давления пара, изме«нения температур кипения н замерзания всегда больше, чем ето отвечает концентрации раствора.

Например, понижение температуры замерзания раствора, со­держащего 1 г NaCl в 100 г воды, почти вдвое превышает Дгзаи, вычисленное по закону Рауля. Во столько же раз и осмотическое давление этого раствора больше теоретической величины.

Как указывалось в § 78, величина осмотического давления вы­ражается уравнением:

Р = CRT

Чтобы распространить это уравнение на растворы с «ненор­мальным» осмотическим давлением, Ванг-Гофф ввел в него попра­вочный коэффициент i (изотонический* коэффициент)¹, показывающий, во сколько раз осмотическое давление данного рас­твора больше «нормального»:

Р = iCRT

Коэффициент i определялся для каждого раствора эксперимен­тальным путем — например, по понижению давления пара, пли по понижению температуры замерзания, или по повышению темпера­туры кипения.

Обозначим через Р' осмотическое давление раствора, через Мши — повышение температуры кипения, Дг_зам — понижение тем­пературы замерзания раствора, не подчиняющегося законам Вант-Гоффа и Рауля, а через Р, Дг_КИп и Дг_зам — значения тех же величин, вычисленные теоретически по концентрации раствора. По­скольку и осмотическое давление, и изменения температур замер­зания н кипения пропорциональны числу находящихся в растворе частиц растворенного вещества, то коэффициент i можно выразить отношениями:

* От греч. «изос» — равный н «тонос» напряжение, давление.

I = Р'/Р = u'_KJ\t_Knn = д4_м/д/_эаи Значения коэффициента £, найденные ВантТоффом для 0,2 н»

растворов некоторых солей по понижению их температур замерза­ния, приведены в табл. 11.

Таблица 11. Значение коэффициента i для 0,2 н. растворов некоторых солей

		Понижение температуры замерзания	л/
Соль	Формула	наблюдаемое К.в)	вычисленное по формуле Рауля (Лгзам)	зам -"зам
Хлорид калия Нитрат калия Хлорид магния Нитрат кальция	КС1 КА'Оз MgCl, Са (\Оз)2	0,673 0,664 0,519 0,461	0,372 0,372 0,186 0,186	1,81 1,78 2,79 2,48

Данные табл. 11 показывают, что коэффициент i для различных солей различен. С разбавлением раствора он растет, приближаясь к целым числам 2, 3, 4. Для солей аналогичного состава эти числа одинаковы. Например, для всех солей, образованных одновалент­ными металлами и одноосновными кислотами, прн достаточном разбавлении их растворов коэффициент i приближается к 2; для солей, образованных двухвалентными металлами и одноосновными кислотами, — к 3.

Итак, соли, кислоты н основания растворяясь в воде, создают значительно большее осмотическое давление, чем эквимолекуляр­ные количества всех остальных веществ. Как же объяснить это явление?

Отметим, что аналогичное явление наблюдаете.! г отношении некоторых газов или веществ, переходящих в газе образное со­стояние. Например, пары пентахлорида фосфора PCl.s, пода и некоторых других веществ при нагревании в закрытом сосуде об­наруживают более высокое давление, чем следует но закону Гей-Люссака.

Для газов это явление объясняется диссоциацией. Если, на­пример, PCI5 полностью разложится на РС1₃ и С1₂, то понятно, что при неизменном объеме давление, зависящее от числа частиц, должно увеличиться вдвое. При неполной диссоциации, когда только часть молекул подверглась разложению, давление также возрастает, но менее, чем вдвое.

Естественно было предположить, что в растворах, обладающих ненормально высоким осмотическим давлением, молекулы раство­ренного вещества тоже распадаются на какие-то более мелкие частицы, так что общее число частиц в растворе возрастает. А по­скольку осмотическое давление зависит от числа частиц раство­ренного вещества, находящихся в единице объема раствора, то с увеличением этого числа оно тоже увеличивается. Такое предпо­ложение впервые было высказано в 1887 г. шведским ученым

Арренпусом * и легло в основу его теории, объясняющей поведение солей, кислот и оснований в водных растворах.

Водные растворы солен, кислот и оснований обладают еще од­ной особенностью — они проводят электрический ток. При этом большинство твердых солен н основании в безводном состоянии, а также безводные кислоты обладают очень слабой электрической проводимостью; плохо проводит электрический ток н вода. Оче­видно, что при образовании растворов подобные вещества претер­певают какие-то изменения, обусловливающие возникновение высо­кой электрической проводимости. Как мы увидим ниже, эти изме­нения заключаются в диссоциации соответствующих веществ на ноны, которые и служат переносчиками электрического тока.

Вещества, проводящие электрический ток своими нонами, на­зываются электролитами. При растворении в воде и в ряде неводных растворителей свойства электролитов проявляют соли, кислоты п основания. Электролитами являются также многие рас­плавленные соли, оксиды и гидроксиды, а также некоторые соли и оксиды в твердом состоянии.

82. Теория электролитической диссоциации. Аррениус обратил внимание на тесную связь между способностью растворов солей, кислот и оснований проводить электрический ток и отклонениями растворов этих веществ от законов Вант-Гоффа и Рауля. Он пока­зал, что по электрической проводимости раствора можно рассчи­тать его осмотическое давление, а следовательно, и поправочный коэффициент /. Значения /, вычисленные им из электрической про­водимости, хорошо совпали с-величинами, найденными для тех же растворов иными методами.

Причиной чрезмерно высокого осмотического давления раство­ров электролитов является, согласно Аррениусу, диссоциация элек­тролитов на ионы. Вследствие этого, с одной стороны, увеличи­вается общее число частиц в растворе, а следовательно, возрастают осмотическое давление, понижение давления пара и изменения температур кипения и замерзания, с другой — ионы обусловли­вают способность раствора проводить электрический ток.

* Сванте Аррениус (1859—1927), профессор университета в Сток­гольме и директор Нобелевского института. Предложил теорию, объясняющую свойства растворов солей, кислот и оснований и получившую название теории Электролитической диссоциации. Аррениусу принадлежит также ряд исследо­ваний по астрономии, космической физике и в области приложений физико-хи­мических законов к биологическим процессам,

Эти предположения в дальнейшем были развиты в стройную теорию, получившую название теории электролитической диссоциации. Согласно этой теории, при растворении в воде электролиты распадаются (диссоциируют) на положительно и от­рицательно заряженные ионы. Положительно заряженные ионы называются катионами; к ним относятся, например, ионы водо­рода и металлов. Отрицательно заряженные ионы называются анионами; к ним принадлежат ионы кислотных остатков и гидроксид-ионы. Как н молекулы растворителя, ионы в растворе находятся в состоянии неупорядоченного теплового движения.

Процесс электролитической диссоциации изображают, поль­зуясь химическими уравнениями. Например, диссоциация НО вы­разится уравнением:

НС1 = Н⁺+ СГ

Распад электролитов па ионы объясняет отклонения от законов Вант-Гоффа и Рауля, о которых говорилось в начале этой главы. В качестве примера мы приводили понижение температуры замер­зания раствора NaCl. Теперь нетрудно понять, почему понижение температуры замерзания этого раствора столь велико. Хлорид нат­рия переходит в раствор в виде ионов Na+ и СР. Прн этом из од­ного моля NaCl получается не 6,02-10²³ частиц, а вдвое большее их число. Поэтому и понижение температуры замерзания в рас­творе NaCl должно быть вдвое больше, чем в растворе неэлектро­лита той же концентрации.

Точно так же в очень разбавленном растворе хлорида бария, диссоциирующего согласно уравнению

ВаС1₂ = Ва²⁺ + 2СГ

осмотическое давление оказывается в 3 раза больше, чем вычис­ленное по закону Вант-Гоффа, так как число частиц в растворе в 3 раза больше, чем если бы хлорид бария находился в нем в виде молекул ВаС1₂.

Таким образом, особенности водных растворов электролитов, противоречащие с первого взгляда законам Вант-Гоффа и Рауля, были объяснены на основе этих же законов.

Однако теория Аррениуса ие учитывала всей сложности явлений в растворах. В частности, она рассматривала ионы как свободные, независимые от молекул растворителя частицы. Теории Аррениуса противостояла химическая, или гидратная, теория растворов Менделеева, в основе которой лежало представление о взаимодей­ствии растворенного вещества с растворителем. В преодолении ка­жущегося противоречия обеих теорий большая заслуга принадле­жит русскому ученому И. А. Каблукову*, впервые высказавшему предположение о гидратации ионов. Развитие этой идеи привело в дальнейшем к объединению теорий Аррениуса и Менделеева,

* Иван_ Алексеевич Каблуков (1857—1942) занимался изучением электрической проводимости растворов. Его работа «Современные теории рас­творов (Вант-Гоффа н Аррениуса) в связи с учением о химическом равнове­сии» оказала большое влияние на развитие физической химии в России и спо­собствовала углублению теории электролитической диссоциации.

83. Процесс диссоциации. В зависимости от структуры раство­ряющегося вещества в безводном состоянии его диссоциация про­текает по-разному. Наиболее типичны при этом два случая. Один из них — это диссоциация растворяющихся солей, т. е. кристаллов

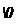
еэ(с1"^ч)ез

с ионной структурой, второй — диссоциация при растворении кис­лот, т. е. веществ, состоящих из полярных молекул.

Когда кристалл соли, например, хлорида калия, попадает в воду, то расположенные иа его поверхности ионы притягивают к себе полярные молекулы воды (ион-диполькое взаимодействие). К ионам калия молекулы воды притягиваются своими отрицатель­ными полюсами, а к хлорид-ионам — положительными (рис. 80). Но, если ионы притягивают к себе молекулы воды, то и молекулы воды с такой же силой притягивают к себе ионы. В то же время притянутые молекулы воды испытывают толчки со стороны других молекул, находящихся в движении. Этих толчков вместе с тепло­выми колебаниями ионов в кристалле оказывается достаточно для отделения ионов от кристалла и перехода их в раствор. Вслед за первым слоем ионов в раствор переходит следующий слой, и таким образом идет постепенное растворение кристалла.

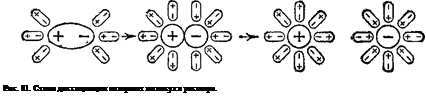
Иначе протекает диссоциация полярных молекул (рис. 81)'. Молекулы воды, притянувшиеся к концам полярной молекулы (ди-поль-дипольное взаимодействие), вызывают расхождение ее полю­сов — поляризуют молекулу. Такая поляризация в сочетании с ко­лебательным тепловым движением атомов в рассматриваемой мо­лекуле, а также с непрерывным тепловым движением окружающих ее молекул воды приводит в конечном счете к распаду полярной молекулы на ионы. Как и в случае растворения ионного кристалла, эти ионы гндратируются. Прн этом ион водорода Н⁺ (т. е. протон); оказывается прочно связанным с молекулой воды в ион гидро-ксония Н₃0⁺. Так, при растворении в воде хлороводорода про­исходит процесс, который схематически можно выразить уравне­нием:

Н₂0 + НС1 = Н₃0⁺ -|- С Г

В результате этого процесса молекула НС1 расщепляется таким образом, что общая пара электронов остается у атома хлора, ко­торый превращается в ион С1~, а протон, внедряясь в электронную оболочку атома кислорода в молекуле воды, образует нон гидро-ксония Н₃0⁺.

Подобного же рода процессы происходят и при растворении в воде других кислот, например, азотной:

Н₂0 + HXOj = Н₃0⁺ + NOj

Перешедшие в раствор ионы остаются связанными с молеку­лами воды и образуют гидраты ионов. Иначе говоря, в резуль­тате диссоциации образуются не свободные ноны, а соединения ионов с молекулами растворителя. В общем случае любого раство­рителя эти соединения называются сел ьв а та ми ионов. Но в уравнениях диссоциации обычно пишут формулы ионов, а не их гидратов или сольватов, тем более что число молекул раствори­теля, связанных с ионами, изменяется в зависимости от концентра­ции раствора и других условий.

Диссоциации веществ как ионного, так и молекулярного строе­ния способствует полярность молекул растворителя. Поэтому не только вода, но и другие жидкости, состоящие из полярных моле­кул (муравьиная кислота, этиловый спирт, аммиак и другие), также являются ионизирующими растворителями: соли, кислоты и основания, растворенные в этих жидкостях, диссоциируют на ионы.

84. Степень диссоциации. Сила электролитов. Если бы электро­литы полностью диссоциировали на ионы, то осмотическое давле­ние (и другие пропорциональные ему величины) всегда было бы н целое число раз больше значений, наблюдаемых в растворах неэлектролитов. Но еще Вант-Гофф установил, что коэффициент i выражается дробными числами, которые с разбавлением раствора возрастают, приближаясь к целым числам.

Аррениус объяснил этот факт тем, что лишь часть электролита диссоциирует в растворе на ионы, и ввел понятие степени дис­социации. Степенью диссоциации электролита называется отно­шение числа его молекул, распавшихся в данном растворе на ионы, к общему числу его молекул в растворе.

Позже было установлено, что электролиты можно разделить на две группы: сильные и слабые электролиты. Сильные электролиты в водных растворах диссоциированы практически нацело. Понятие степени диссоциации к ним по существу неприменимо, а отклоне­ние изотонического коэффициента I от целочисленных значений объясняется другими причинами (см. § 86). Слабые электролиты в водных растворах диссоциируют только частично, и в растворе устанавливается динамическое равновесие между недиссоцииро-ванными молекулами п нонами.

К сильным электролитам принадлежат почти все соли; из важ­нейших кислот и оснований к ним относятся HN0₃, H₂S0₄, НСЮ₄, НС1, НВг, HI, КОН, NaOH, Ва(ОН)₂ и Са(ОН)₂.

К слабым электролитам относится большинство органических кислот, а из важнейших неорганических соединений к ним принад­лежат Н₂СОз, H₂S, HCN, H₂Si0₃ и NH₄OM.

Степень диссоциации принято обозначать греческой буквой а и выражать либо в долях единицы, либо в процентах. Так, для 0,1 н. раствора СН₃СООН а ==0,013 (или 1,3%), а для 0,1 н. рас­твора HCN а = Ю-⁴ (или 0,01 %).

85. Константа диссоциации. К равновесию, которое устанавли­вается в растворе слабого электролита между молекулами и иона­ми, можно применить законы химического равновесия и записать выражение константы равновесия. Например, для диссоциации уксусной кислоты

СНзСООН ==!= Н⁺ -|- СНзСОСГ

константа равновесия имеет вид

[Н⁺] [сНзСОО-] ^{А =} [СНзСООН]

Здесь в числителе дроби стоят концентрации ионов—■продук­тов диссоциации, а в знаменателе — концентрация недиссоцииро-ваиных молекул.

Константа равновесия, отвечающая диссоциации слабого элек­тролита, называется константой диссоциации. Величина К зависит от природы электролита и растворителя, а также от тем­пературы, но не зависит от концентрации раствора. Она характе­ризует способность данной кислоты или данного основания распа­даться на ионы: чем выше Л', тем легче электролит диссоциирует*

Мнсгоссновные кислоты, а также основания двух- и более ва­лентных металлов диссоциируют ступенчато. В растворах эти}8 веществ устанавливаются сложные равновесия, в которых участи вуют ионы различного заряда. Например, диссоциация угольной кислоты происходит в две ступени:

Н₂С0₃ H⁺ + HCOJ

НСО3- =ё=!= н⁺ + со|"

Первое равновесие — диссоциация по первой ступе* ни — характеризуется константой диссоциации, обозначаемой Kii

_к,. Е?.Н"^С(>»"1

а второе — диссоциация по второй ступени — констан­той диссоциации -Кг:

[Н⁺] [СО?"]

Аг = —f;—

[нсо;]

Суммарному равновесию

н₂со₃ +=± 2н⁺ + со:г

отвечает суммарная константа диссоциации К:

У [Hi [СОГ] 1Н_гС0₃]

Величины К, К\ и Кг связаны друг с другом соотношением:

к = к,к_г

Аналогичные соотношения характеризуют и ступенчатую диссо­циацию оснований многовалентных металлов. Например, двум сту­пеням диссоциации гидроксида железа(II)

Fe(OH)₂ FcOH⁺ + OH~

FeOH⁺ <=± Feⁱ⁺ + OH"

отвечают константы диссоциации:

.. [FeOH⁺][Oir] „ [Fe²⁺][OHl

Л I = -------------------------------------------- ■ И l\2

[Fe(OH)₂] [FeOH⁺]

Суммарной диссоциации

Fe(OH)_a Fe²⁺ + 20H"

отвечает константа:

[Fe(0H)₂]

При этом

/< = KiK₂

При ступенчатой диссоциации веществ распад по последующей ступени всегда происходит в меньшей степени, чем по предыдущей (по второй меньше, чем по первой и т. д.). Иначе говоря, соблю­дается неравенство:

К^ЖгЖг...

Это объясняется тем, что энергия, которую нужно затратить для отрыва иона, минимальна при его отрыве от нейтральной молекулы и становится больше при диссоциации по каждой сле­дующей ступени.

Если обозначить концентрацию электролита, распадающегося на два иона, через С, а степень его диссоциации в данном рас­творе через а, то концентрация каждого из ионов будет Са, а кон­центрация недиссоциированных молекул С(1 — а). Тогда уравне-

К =

ние константы диссоциации принимает вид (Са)²

С (1 — а)

1 — а

Это уравнение выражает закон разбавления Оствальда. Оно дает возможность вычислять степень диссоциации при различ­ных концентрациях электролита, если известна его константа дис­социации. Пользуясь этим уравнением, можно также вычислить константу диссоциации электролита, зная его степень диссоциации при топ или иной концентрации.

Для растворов, в которых диссоциация электролита очень мала, уравнение закона Оствальда упрощается. Поскольку в таких случаях а <С 1, то величиной а в знаменателе правой части урав­нения можно пренебречь. При этом уравнение принимает вид: К = а²С или asV К/С

Это уравнение наглядно показывает связь, существующую ме­жду концентрацией слабого электролита и степенью его диссоциа­ции: степень диссоциации возрастает при разбавлении раствора.

Полученный вывод вытекает из природы явления диссоциации. Как всякое химическое равновесие, равновесие в растворе слабого электролита является динамическим, т. е. при его установлении протекают с равными скоростями два процесса: процесс диссоциа­ции и обратный ему процесс образования молекул из ионов. При этом разбавление раствора не препятствует первому из этих про­цессов—диссоциации. Однако процесс образования молекул из попов в результате разбавления затрудняется: для образования молекулы должно произойти столкновение ненов, вероятность ко­торого с разбавлением уменьшается.

Таблица 12. Константы диссоциации некоторых слабых электролитов в водны;: растворах при 25 "С

Дата добавления: 2014-11-16