Расчет зубчатых колес редуктора

Выбор материалов и термической обработки зубчатых колес

Для изготовления зубчатых колес в основном применяются углеродистые и легированные стали. Механические свойства сталей, применяемых для изготовления зубчатых колес, приведены в табл. 3.10.

При выборе материалов учитывают, что у шестерни число циклов нагружения и напряжения изгиба больше, чем у колеса. Поэтому для обеспечения равнопрочности элементов передачи, а также устранения задиров и заеданий, необходимо, чтобы у прямозубых передач с Н £ 350 НВ твердость шестерни превышала твердость колеса на 25…50 единиц НВ, а у косозубых и шевронных – на 50…100 единиц (в редукторах общего назначения применяют колеса с твердостью зубьев Н £ 350 НВ). Для колес с твердостью Н £ 350 НВ назначают марки сталей, подвергающиеся улучшению, редко – нормализации. Для колес с твердостью Н > 350 НВ назначаются марки сталей, подвергающиеся закалке с нагревом током высокой частоты, цементации, азотированию.

В зависимости от вида редуктора, условий его эксплуатации и требований к габаритным размерам выбирают необходимую твердость колес и соответствующий вариант термической обработки (т.о.) [2]: I т.о. колеса –улучшение, твердость НВ 235¼262; т.о. шестерни – улучшение, твердость НВ 269¼302. Марки сталей одинаковы для колеса и шестерни: 45, 40Х, 40ХН, 35 ХН и др.; II т.о. колеса – улучшение, твердость НВ 269¼302; т.о. шестерни – улучшение и закалка ТВЧ, твердость в зависимости от марки стали (см. табл. 3.10) НRС 45¼50; 48¼53. Марки сталей одинаковы для колеса и шестерни: 45, 40Х, 40ХН, 35 ХН и др.; III т.о. колеса и шестерни одинаковая – улучшение и закалка ТВЧ, твердость поверхности в зависимости от марки стали: НRС 45¼50; 48¼53. Марки сталей одинаковы для колеса и шестерни: 40Х, 40ХН, 35 ХН и др.; IV т.о. колеса – улучшение и закалка ТВЧ, твердость поверхности в зависимости от марки стали (см. табл. 3.10) НRС 45¼50; 48¼53; т.о. шестерни – улучшение, цементация и закалка, твердость поверхности НRС 56¼63. Материал шестерни – сталь марки 20Х, 20ХН2М, 18ХГТ, 12ХН3А и др.; V т.о. колеса и шестерни одинаковые – улучшение, цементация и закалка, твердость поверхности НRС 56¼63. Марки сталей одинаковы для колеса и шестерни: 20Х, 20ХН2М, 18ХГТ, 12ХН3А, 25ХГН и др.

Чем выше твердость рабочей поверхности зубьев, тем выше допускаемые контактные напряжения и тем меньше размеры передачи. Поэтому для редукторов, к размерам которых не предъявляют особых требований, следует применять дешевые марки сталей типа 45 и 40Х с т.о. по вариантам I или II.

Таблица 3.10

Марка стали	Термическая обработка	Твердость НВ (средняя)	Предел прочности σв, МПа	Предел текучести σт, МПа	Диаметр заготовки, мм
	Нормализация				До 80 100 – 500
	Улучшение				До 90 90 – 120 св. 120
40ХН, 35ХМ	Улучшение				До 150 150-180 св. 180
Марка стали	Твердость НRC	Термообработка
40Х, 40ХН, 35ХМ, 20ХГМ, 18ХСТ, 12ХМ3А, 25ХГМ	45-55 56-67	Закалка Улучшение, цементация, закалка

Допускаемые напряжения

Расчет закрытых зубчатых передач ведут по допускаемым контактным напряжениям, а проверочный расчет производят по напряжениям на контактную и изгибную прочность.

Допускаемые контактные напряжения

[σ _H ] = σ _{H lim b} × K_HL × Z_R × Z_v / [ S_н ],

где σ _{H lim b} — предел контактной выносливости при базовом числе циклов (табл. 3.11); [ S_Н ] – коэффициент безопасности; Z_R – коэффициент, учитывающий шероховатость сопряженных поверхностей зубьев; Z_v – коэффициент, учитывающий окружную скорость передачи; К_НL – коэффициент долговечности.

Таблица 3.11

Химико-термическая или термическая обработка	Марки сталей	Твердость	σ H lim b, МПа	σF lim b, МПа	[ S F]
Нормализация, улучшение	45; 40X; 40XH; 35XM	Н < 350 НВ	2НВ+70	1,8 НВ	1,75
Закалка ТВЧ по контуру зубьев	40Х; 40ХН; 35ХМ	Н = 40…50 НRСэ	17HRCэ+200		1,75
Объемная закалка	Н = 38…50 НRСэ	18HRCэ+150		1,8
Цементация и закалка	20Х; 20ХН2М; 18ХГТ; 12ХН3А; 25ХГМ	H > 56 НRСэ	23HRC		1,55

Коэффициент безопасности зубчатых колес с однородной структурой материалов S_Н = 1,1 с поверхностным упрочнением зубьев, S_Н = 1,2. Коэффициент Z_R = 0,9¼1,0 (Z_R = 0,95 при R_а = 2,5¼1,25; Z_R = 0,9 при

R_а = 10¼5). Коэффициент Z_v = 1 ¼1,16; чем меньше скорость передачи и тверже зубья, тем меньше Z_v. При v £ 5 м/с Z_v = 1. Коэффициент К_НL определяют из диаграммы (рис. 3.2) в зависимости от отношения N_НE / N_{Н 0}, где N_НE – эквивалентное число циклов напряжения в зубьях, соответствующее рабочему числу циклов передачи с постоянным режимом нагружения, а N_{Н 0} – базовое число циклов напряжений в зубьях, которое принимают по графику (рис. 12.21 [1]) в зависимости от твердости НВ рабочей поверхности зубьев или вычисляют по формуле

N_{Н 0} = 30 × Н ^2,4_НВ £ 120×10⁶.

Эквивалентное число циклов напряжений при работе передачи с постоянной нагрузкой

N_НE = 60 × с × n × t,

где с – число одинаковых зубчатых колес, сцепляющихся с рассчитываемым зубчатым колесом; n – частота вращения рассчитываемого зубчатого колеса, об/мин; t – продолжительность работы передачи под нагрузкой за расчетный срок службы, ч; при передаче с переменными нагрузками

где Т _max – максимальный крутящий момент, передаваемый зубчатым колесом в течение времени t за весь срок службы передачи частоте вращения колеса n; Т ₁, Т ₂, ¼, Т_i – передаваемые зубчатым колесом крутящие моменты в течение времени t ₁, t ₂, ¼, t_i при частоте вращения n ₁, n ₂, ¼, n_i.

Коэффициент долговечности определяют по формулам:

при N_НE < N_{Н 0}

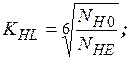
при N_НE > N_{Н 0}

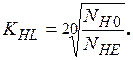
Предельные значения К_НL ограничиваются [5]. Для стальных колес К_НL £ 2,6 при объемном упрочнении и К_НL £ 1,8 при поверхностном упрочнении. При N_НE / N_{Н 0}> 1 коэффициент долговечности К_НL = 1.

В качестве допустимого контактного напряжения для прямозубых колес принимают меньшее из двух: [σ _{Н 1}] и [σ _{Н 2}]. Для прямозубых колес расчетное допускаемое контактное напряжение

[σ _Н ] = 0,45 × ([σ _{Н 1}] + [σ _{Н 2}]),

где [σ _{Н 1}] и [σ _{Н 2}] – допускаемые контактные напряжения соответственно шестерни и колеса.

После их определения следует проверить выполнение условия

[σ _Н ] £ 1,23 × [σ_min],

где [σ_min] – меньшее допускаемое контактное напряжение из двух [σ _{Н 1}] и [σ _{Н 2}], как правило, равно [σ _{Н 2}].

Допускаемые напряжения при расчете на выносливость
зубьев при изгибе

Методика выбора допускаемых напряжений приведена в ГОСТ 21354–75. Для редукторов общего назначения пользуются формулой

[σ _F ] = σ _{F lim b} × К_FL × К_FC / S_F,

где σ _{F lim b} – предел выносливости зубьев при изгибе, соответствующий базовому циклу напряжений (табл. 3.11); S_F – коэффициент безопасности (табл. 3.11); К_FL – коэффициент долговечности; К_FC – коэффициент, учитывающий влияние двустороннего приложения нагрузки на зубья; при одностороннем действии К_FC = 1.

Коэффициент долговечности

где N_{F 0} и N_FE – соответственно базовое и эквивалентное число циклов напряжений. Для зубчатых колес с твердостью поверхности зубьев НВ£350, а также со шлифованной переходной поверхностью зубьев показателя корня m = 6, для зубчатых колес с НВ>350 и нешлифованной переходной поверхностью m =9. Базовое число циклов напряжений N_{F 0} = 4×10⁶ Мпа. Эквивалентное число циклов перемены напряжений N_FE при работе передачи с постоянной нагрузкой

N_FE = 60 × с × n × t,

где с – число одинаковых колес, сцепляющихся с рассчитываемым зубчатым колесом; n – частота вращения рассчитываемого зубчатого колеса, об/мин; t – продолжительность работы передачи под нагрузкой за расчетный срок службы.

Эквивалентное число циклов перемены напряжений N_FE при работе передачи с переменными нагрузками

N_FE =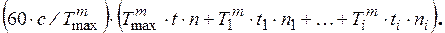

При N_FE > N_{F 0} принимают К_FL = 1.

Значение коэффициента К_FС принимают: при односторонней нагрузке на зубья К_FС = 1, а при двусторонней К_FС = 0,7¼0,8 (большее значение при НВ>350).

Расчет зубьев на изгиб производят по тому зубчатому колесу, для которого отношение [s _F ] / У_F имеет меньшее значение.

Допускаемое максимальное напряжение на изгиб зубьев при твердости поверхностей зубьев НВ£350 [s _F ]_max = 0,86s_т, где s_т – предел текучести материала зубьев при растяжении; при твердости НВ>350 [s _F ]_max= 0,86s_в, где s_в – предел прочности материала при растяжении (табл. 3.10).

Последовательность проектировочного расчета

При проектировочном расчете определяют ориентировочное значение межосевого расстояния

,

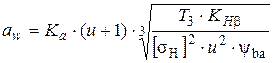где для прямозубых передач К _a = 49,5, для косозубых и шевронных передач К _a = 43,0; передаточное число зубчатой передачи u = u ₂; Т ₃ — крутящий момент на валу колеса Н×мм; К _Hβ — коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца (рис. 3.1);

ψ_ba = b / a_w — коэффициент ширины венца по межосевому расстоянию, для прямозубых передач принимают ψ_ba = 0,125…0,25, для косозубых ψ_bа = 0,25…0,4, для шевронных ψ_ba = 0,5…1,0 (ГОСТ 2185-66, ряд 0,100; 0,125; 0,160; 0,250; 0,315; 0,400; 0,500; 0,800; 1,00; 1,25).

После определения межосевого расстояния а_w, мм, его округляют до ближайшего значения по ГОСТ 2185–66.

Первый ряд: 40, 50, 63, 80, 100, 125, 160, 200, 250, 315, 400, 500, 630, 800, 1000, 1250, 1600, 2000, 2500.

Второй ряд: 71, 90, 112, 140, 180, 224, 280, 355, 450, 560, 710, 900, 1120, 1400, 1800, 2240.

Первый ряд следует предпочесть второму.

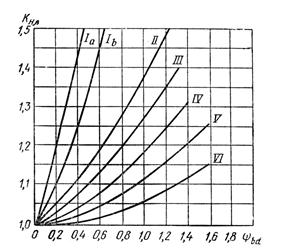
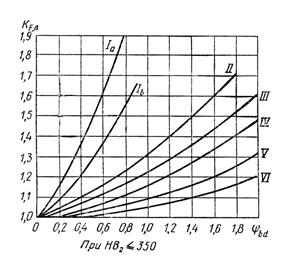
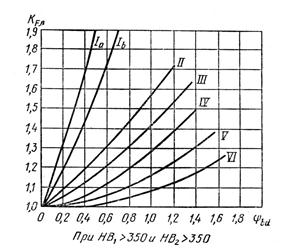
Рис. 3.1

Выбирают модуль m, мм, в интервале (ГОСТ 9563—60)

m_n = (0,01 – 0,02) × а_w.

Первый ряд: 1; 1,25; 2; 2.5; 3; 4; 6; 8; 10; 12; 10; 20.

Второй ряд: 1,375; 1,75; 2,25; 2,75; 3,5; 4,3; 7;9; 11; 14; 18; 22.

Первый ряд предпочтительней второго.

Для косозубых колес стандартным считают нормальный модуль m_n.

Для шевронных колес стандартным может быть как нормальный модуль m_n, так и окружной m_t. = m_n / сosb.

Определение чисел зубьев колес

Суммарное число зубьев z _Σ = z ₁ + z ₂.

У прямозубой передачи z _Σ = (2 × а_w) / m_n; z ₁ = z _Σ / (u + 1),
z ₂ = z _Σ – z ₁; полученные значения округляют до целых чисел. Величину z ₁ сравнивают с рекомендуемыми значениями по табл. 3.12.

Если после выбора z ₁ и z ₂ величина а_w = (m × z _Σ) / 2 будет отличаться от принятого стандартного значения, то можно принять новый модуль из рекомендуемого диапазона (см. выше) и повторить расчет.

Таблица 3.12

Частота вращения шестерни n 1, об/мин	Рекомендуемое минимальное число зубьев шестерни z 1
Прямозубой	Косозубой
>1000	24…26	20…22
500…1000	22…24	18…20
100…500	18…22	16…18
<100	17…18

Для косозубых и шевронных колес со стандартным нормальным модулем

z _Σ = (2 × а_w × cosβ) / m_n.

Угол наклона линии зуба принимают для косозубых колес в интервале β = 8…15°, для шевронных β = 25…40°. Определяют значение z ₁= z _Σ/(u +1) и z ₂ = z _Σ – z ₁. По округленным значениям z ₁ и z ₂ уточняют передаточное число u = z ₂ / z ₁.Затем находят с учетом окончательно принятого z _Σ значения cosβ = (z _Σ × m_n) / (2 × a_w) и торцового модуля m_t = m_n / cosβ. Вычисления выполняют с точностью до пятого знака после запятой.

Направление зуба в косозубых передачах рекомендуется принимать для колес правое, а для шестерни — левое. Проверку межосевого расстояния для косозубых и шевронных колес с нормальным стандартным модулем осуществляют по формуле

а _w = 0,5 × (z ₁ + z ₂) × (m_n / cosβ).

Основные размеры, степень точности шестерни и колеса (рис. 3.2). Силы, действующие в зацеплении.

Диаметры делительные находят из равенства d ₁ = (m_n / cosβ) × z ₁; d ₂ = (m_n / cosβ) × z ₂; проверка а_w = (d ₁ + d ₂) / 2.

Диаметры вершин зубьев d_{a 1} = d ₁ + 2 × m_n; d_{a 2} = d ₂ + 2 × m_n.

Диаметры впадин d_{f 1} = d ₁ – 2,5 × m_n; d_{f 2} = d ₂ – 2,5 × m_n.

Ширина колеса b ₂ = ψ _bа × а_w; полученные значения округляют до большего ближайшего числа из ряда (Ренора) R_a 20 (22; 25; 28; 40; 45; 50; 56; 63; 71; 80; 90; 100; 110; 125; 140; 160; 180; 200;) или R_a 40 (11; 13; 15; 17; 19; 21; 24; 26; 30; 34; 38; 42; 48; 53; 60; 67; 75; 85; 95; 105; 120; 130; 150; 170; 190), ГОСТ 6636–69.

Ширина шестерни b ₁ = b ₂ + 5 мм.

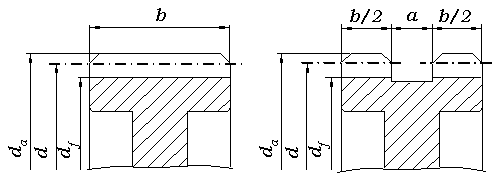
Рис. 3.2

Для шевронных зубчатых колес, выполняемых с канавкой посредине, предназначенной для выхода червячной фрезы, нарезающей зубья, ширину а канавки определяют по отношению а / m:

m, мм ……………… 2 3 4 5 6

а / m ……………….. 15 14 13 12 10

Коэффициент ширины шестерни по диаметру ψ _bd = b ₁ / d ₁, окружная скорость в зацеплении, м/с,

v = (ω₁ × d ₁) · 10 ^–3 / 2.

Используя значения окружной скорости, по табл. 3.13 уточняют степень точности передачи и по формулам табл. 3.14 определяют силы, действующие в зацеплении.

Проверка зубьев на контактную выносливость

Проверочный расчет на контактную выносливость рабочих поверхностей зубьев состоит в определении контактных напряжений σ _Н на рабочих поверхностях зубьев и сопоставление их с допускаемыми [σ _Н ]:

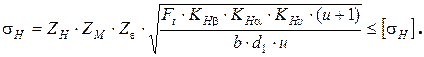
Таблица 3.13

Степень точности зубчатых колес (по ГОСТ 1613-81)	Окружная скорость передачи v, м/с
прямозубой	непрямозубой
цилиндрической	конической	цилиндрической	конической
5 и более точные	> 15	> 12	> 30	> 20
	£ 15	£ 12	£ 30	£ 20
	£ 10	£ 8	£ 15	£ 10
	£ 6	£ 4	£ 10	£ 7
	£ 2	£ 1,5	£ 4	£ 3

Таблица 3.14

Сила, Н	Вид передач
Прямозубая	Косозубая или шевронная
Окружная	Ft = 2 T 1 × 10^3 / dw 1 = 2 T 2 × 10^3 / dw 2
Радиальная	Fr = Ft × tga w	Fr = Ft × tga w /cosb
Осевая	—	Fx = Fa = Ft × tgb

Коэффициент Z_H учитывает форму сопряженных поверхностей зубьев, Z_H = 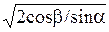; b – основной угол наклона зуба; a – угол зацепления, a = 20°.

Коэффициент Z_М учитывает механические свойства материалов сопряженных колес. Для зубчатой передачи со стальными зубчатыми колесами Z_М = 190.

Коэффициент Z _e учитывает суммарную длину контактных линий. При e_b < 0,9 Z _e = 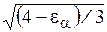; e_b > 0,9 Z _e = .

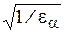Коэффициент торцевого перекрытия

e_a = [1,88 – 3,2 (1/ Z ₁ + 1/ Z ₂)]×сosb.

Коэффициент осевого перекрытия

e_b = b ×sinb / p× m.

Окружное усилие в зацеплении F_t, Н×мм – табл. 3.14. Значение коэффициента К_{Н β} определяют по табл. 1.15 или по графику рис. 3.2.

Коэффициент К_{Н α}, учитывающий распределение нагрузки между зубьями, определяют по табл. 3.16.

Коэффициент К_Нv, учитывающий динамическую нагрузку, возникающую в зацеплении, определяют по табл. 3.17 или по формуле

К_Нv = 1 + w_Нv × b / F_t × К_{Н α} × К_{Н β},

где w_Нv – удельная окружная динамическая сила, Н/мм.

w_Нv = d _Н × g ₀ × v × .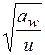

Коэффициенты d _Н и g ₀ выбираются по табл. 10,4, 10.5 [4]

Вычисленное контактное напряжение сравнивают с допускаемым

Ds = {([s_H] – s_H)/ [s_H]}×100%.

Допускаемое максимальное контактное напряжение

[s_H]_max = 2,8 × s_т МПа,

где s_т – предел текучести (табл. 3.10).

Так как кратковременная нагрузка передачи больше номинальной в раза, то проверяют условие прочности по максимальной нагрузке

s_Hmax = s_H × < [s_H]_max.

Проверка зубьев на выносливость по напряжениям изгиба. Условие выносливости по напряжениям изгиба:

σ _F = (F_t × K_F × Y_F × Y _β × K_Fα) / (b × m_n) £ [σ _F ].

Окружное усилие в зацеплении F_t, Н×мм – табл. 3.14. Значение коэффициента К_F = K_{F β} × K_Fv определяют по табл. 3.15 или по графику рис. 3.1.

Коэффициент нагрузки К_F = K_{F β} × К_Нv, где K_{F β} — коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба (коэффициент концентрации нагрузки); К_Нv — коэффициент, учитывающий динамические действия нагрузки (коэффициент динамичности).Значения коэффициентов К_{F β} приведены в табл. 3.18, составленной на основании графиков ГОСТ 21354–75 с некоторыми упрощениями. Ориентировочные значения коэффициента динамичности К_Нv приведены в табл. 3.19.

Таблица 3.15

yвd = b / d 1	Твердость поверхности зубьев
Н £ 350 НВ	Н > 350 НВ
I	II	III	I	II	III
KH b
0,4	1,15	1,04	1,0	1,33	1,08	1,02
0,6	1,24	1,06	1,02	1,50	1,14	1,04
0,8	1,30	1,08	1,03	—	1,21	1,06
1,0	—	1,11	1,04	—	1,29	1,09
1,2	—	1,15	1,05	—	—	1,12
1,4	—	1,18	1,07	—	—	1,16
1,6	—	1,22	1,09	—	—	1,21
1,8	—	1,25	1,11	—	—	—
2,0	—	1,30	1,14	—	—	—
Примечание: I — к передачам с консольным расположением зубчатых колес; II — к передачам c несимметричным расположением колес по отношению к опорам; III — к передачам c симметричным расположением колес

Таблица 3.16

Степень точности зубчатых колес	Окружная скорость v, м/с
£ 1
КH a для косозубых и шевронных передач
		1,02	1,03	1,04	1,05
	1,02	1,05	1,07	1,10	1,12
	1,06	1,09	1,13	—	—
	1,1	1,16	—	—	—
Для прямозубых колес КH a = 1

Таблица 3.17

Передача	Твердость Н поверхности зубьев	Окружная скорость v, м/с
До 5
Степень точности зубчатых колес
КНv
Прямозубая	Н £ 350 НВ Н > 350 НВ	1,05 1,10	—	—	—
Косозубая и шевронная	Н £ 350 НВ Н > 350 НВ	1,0 1,0	1,0 1,05	1,02 1,07	1,05 1,10

Коэффициент, учитывающий форму зуба Y_F для зубчатых колес, выполненных без смещения, имеет следующие значения:

z 17 20 25 30 40 50 60 70 80 100 и более

Y_F 4,28 4,93 3,90 3,80 3,70 3,66 3,62 3,61 3,61 3,6

Для непрямозубых передач значение Y_F выбирают по эквивалентному числу зубьев z_v = z / cos³ β.

Коэффициент Y _β компенсации погрешности определяют по формуле:

Y _β = 1 – (β° / 140),

где β – угол наклона делительной линии зуба, град.

Коэффициент K_{F α} учитывает неравномерность распределения нагрузки между зубьями.

Для зубчатых колес, у которых коэффициент осевого перекрытия

ε_β = (b × tg β) / (π × m_t) < 1, K_{F α} = 1,0.

При ε_β 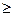1:

К_{F α} = [4 + (ε_α – 1) × (n – 5)] / (4 × ε_α),

где ε_α — коэффициент торцового перекрытия; n — степень точности зубчатых колес.

При среднем значении ε_α = 1,5 и 8-й степени точности К_{F α} = 0,92.

Таблица 3.18

yвd = b / d 1	Твердость Н рабочих поверхностей зубьев
Н £ 350 НВ	Н > 350 НВ
I	II	III	IV	I	II	III	IV
KF b
0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8	1,00 1,03 1,05 1,08 1,10 1,13 1,19 1,25 1,32	1,04 1,07 1,12 1,17 1,23 1,30 1,38 1,45 1,53	1,18 1,37 1,62 — — — — — —	1,10 1,21 1,40 1,59 — — — — —	1,03 1,07 1,09 1,13 1,20 1,30 1,40 — —	1,05 1,10 1,18 1,28 1,40 1,53 — — —	1,35 1,70 — — — — — — —	1,20 1,45 1,72 — — — — — —
Примечание: I — к симметричному расположению зубчатых колес относительно опор; II — к несимметричному; III — к консольному при установке валов на шариковых подшипниках; IV — то же, что и при установке валов на роликовых подшипниках.

Таблица 3.19

Степень точности зубчатых колес	Твердость Н рабочей поверхности зубьев	Окружная скорость v, м/с
£ 3	3…8	8…12,5
КFv
	Н £ 350 НВ Н > 350 НВ	1/1 1/1	1,2/1 1,15/1	1,3/1 1,25/1
	Н £ 350 НВ Н > 350 НВ	1,15/1 1,15/1	1,35/1 1,25/1	1,45/1,2 1,35/1,1
	Н £ 350 НВ Н > 350 НВ	1,25/1,1 1,2/1,1	1,45/1,3 1,35/1,2	– /1,4 – /1,3
Примечание: в числителе приведены значения КFv для прямозубых передач, в знаменателе – для косозубых

Дата добавления: 2014-11-16