Предмет теории вероятностей. Частота. Геометрическая вероятность

Случайные события, операции над событиями и отношения между ними. Пространство элементарных событий. Классическое определение вероятности. Теорема сложения вероятностей.

Теория вероятностей занимается изучением случайных событий и их вероятностей.

Будем говорить, что производится испытание (опыт, эксперимент, наблюдение), если осуществляется некоторая совокупность условий, в результате чего могут происходить какие-то события.

Примеры испытаний: 1)бросание одной или нескольких монет (или кубиков), 2) выбор наугад из заданной однородной группы предметов (урна с шарами, колода карт, партия деталей и т.п.) некоторого меньшего количества этих предметов, 3)стрельба по мишени.

Основным понятием в теории вероятностей является понятие случайного события. Событие называется случайным, если в результате испытания оно может произойти или не произойти (см. также с.5).

Все события можно разделить на три типа:

невозможное событие (обозначим его - Æ) - это такое событие, которое в результате испытания не может произойти,

достоверное событие (обозначим его W) - это событие, которое в результате испытания обязательно происходит. Наконец, основная масса событий – это

случайные события (их обычно обозначают А, В, С...), т.е. такие, которые в результате испытания могут произойти, а могут и не произойти.

Вероятность P(A) случайного события А - это число, отражающее меру возможности появления события А в данном испытании.

Отметим, что

0 Р(А) 1,

Р( Æ )= 0, Р(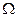) = 1.

Рассмотрим некоторое испытание и связанное с ним случайное событие А. Предположим, что это испытание произведено многократно при неизменных условиях. Пусть n - число всех проведенных испытаний, k - число испытаний, при которых событие А произошло.

Относительной частотой (частостью) события А в этой серии испытаний называется число

w = .

Длительные наблюдения показывают, что имеет место свойство устойчивости относительных частот:

1) при проведении нескольких серий из n испытаний относительные частоты каждой из этих серий будут примерно одинаковыми и

2) с увеличением числа испытаний n относительные частоты все меньше и меньше будут отклоняться друг от друга.

Если эти относительные частоты разумным образом округлить, то полученное таким образом число P(А) называют статистической вероятностью события А. Условно эту процедуру можно обозначить так:

P(A) = .

Статистическое определение вероятности используют в качестве оценки вероятности, но оно требует больших затрат времени. Однако в некоторых случаях статистическое определение является единственной пригодным.

Например, пусть испытанием является бросание заведомо несимметричного кубика или кубика, у которого центр тяжести смещен относительно геометрического центра (фальшивая игральная кость). В этом случае вероятности выпадения каждой из шести граней можно найти только статистически.

Проведение повторных испытаний может быть сопряжено с большими материальными затратами или невозможно. Поэтому важно уметь находить вероятность случайного события без проведения испытаний, а лишь используя знание о возможных результатах проведенного испытания.

Пространством элементарных исходов (событий) W некоторого испытания (опыта) будем называть множество всех возможных результатов проведения этого испытания.

Примеры.

№	Испытание	Случайные события	Пространство элементарных исходов W
	Монету подбрасывают два раза	А - число орлов и решек будет поровну В - выпадет хотя бы один орел С - обе монеты выпадут орлом
	Кубик (игральную кость) бросают два раза	А - выпадет хотя бы одна шестерка В - сумма выпавших очков будет меньше десяти С - выпадут две единицы
	Из колоды в 36 карт достают наугад три карты	А - все три карты будут одной масти В - хотя бы одна из трех карт является тузом С - все три карты будут разного достоинства
	Из урны, содержащей 4 белых и 6 черных шаров, достают по очереди наугад 3 шара	А - все шары будут одного цвета В - цвета шаров будут чередоваться С - среди вынутых шаров белых больше, чем черных
	Производится один выстрел в тире	А - попадание в мишень	Стена в тире, на которой установлена мишень

В случаях примеров испытаний 3),4) пространства W содержат большое число элементов, которое находят, применяя формулы комбинаторики (см. стр. 12).

Понятие пространства элементарных исходов используется для определения понятия случайного события.

Случайным событием называется всякое подмножество А пространства элементарных исходов W некоторого испытания.

Случайное событие А происходит, если в результате испытания имеет место один из исходов события А. Поэтому исходы, входящие в событие А называются благоприятствующими событию А.

Случайное событие можно задать указанием характеристического свойства, как это было сделано в примерах 1) – 5) или в простых случаях, например, 1) и 2) перечислением исходов благоприятствующих случайному событию:

№	Испытание	Случайные события
	Монету подбрасывают два раза	А - число орлов и решек будет поровну А = В – выпадет хотя бы один орел В = 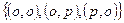С – обе монеты выпадут орлом С =
	Кубик (игральную кость) бросают два раза	А – выпадет хотя бы одна шестерка А = В – сумма выпавших очков будет меньше десяти В = С – выпадут две единицы, С =

В теории вероятностей над случайными событиями производятся операции. Будет использоваться геометрическая интерпретация этих операций на примере испытания - неприцельной стрельбы в тире. Пусть W - ограниченная область на плоскости (например, - стена в тире). Испытание состоит в том, что внутри области W наугад отмечается точка М (выстрел наудачу). Тогда каждому подмножеству А (мишень) в W соответствует (случайное) событие А, состоящее в том, что точка М попадет в А. Определим операции над случайными событиями:

1) суммой событий А и В называется событие A+B, состоящее в том, что в результате испытания произойдет хотя бы одно из событий А или В. Геометрически сумма событий соответствует объединению подмножеств А и В.

W

A B

A+B

Рис. 1

2) произведением событий А и В называется событие А×В, состоящее в том, что в результате испытания произойдут оба этих события А и В одновременно. Этой операции геометрически соответствует пересечение подмножеств А и В.

W

A B

A×B

Рис. 2

Случайные события А и В называются несовместными (несовместимыми), если в результате испытания они не могут произойти одновременно, т.е. А × В =Æ. (геометрически это означает, что подмножества А и В не пересекаются).

Если же А.В Æ, то события А и В называются совместными (Рис. 2). Так, например, в рассматриваемых выше примерах совместными являются следующие пары событий:

в 1-м испытании - А и В, В и С; во 2-м испытании - А и В, В и С;

несовместными являются следующие пары событий:

в 1-м испытании - А и С; в 4-м испытании - А и С;

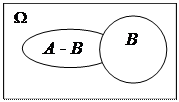
3) разностью событий А и В называется событие А - В, состоящее в том, что в результате испытания произойдет событие А, а событие В не произойдет. Этой операции геометрически соответствует дополнению подмножества В в А..

АА

4) событием, противоположным к событию А, называется событие состоящее в том, что в результате испытания событие А не произойдет. Т.е. соответствует дополнению А в W или =W- А.

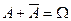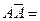Событие удовлетворяет также следующим соотношениям: и Æ.

W

A

Множество всех случайных событий с введенными операциями называется алгеброй событий.

Дата добавления: 2014-11-16