Формула полной вероятности. Рассмотрим некоторое испытание, в результате которого может произойти событие А одновременно с одним из событийН1

Рассмотрим некоторое испытание, в результате которого может произойти событие А одновременно с одним из событийН₁, Н₂,..., Н_n- полной группы несовместных событий (обычно их называют гипотезами).

1) Н_i H_j Æ,

2) H₁ + H₂ + … + H_n = W.

Событие А можно представить в виде суммы несовместных событий:

А=АН₁+АН₂+...+АН_n. H₁ H₂ H₃

AH₂

AH₁ AH₃

AH_n

H_n …

Применив к этому равенству последовательно формулы сложения и умножения вероятностей, получим формулу:

=

=

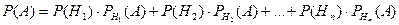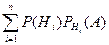
которая называется формулой полной вероятности.

Рассмотрим примеры.

Задача 1. В тире имеется 10 ружей. Для пяти из них вероятность попадания в цель равна 0.8, для трех других - 0.6 и для двух оставшихся - 0.3. Человек, зайдя в тир, выбирает наугад ружье и стреляет из него по цели. Найти вероятность того, что цель будет поражена.

Решение. Для удобства будем называть ружья хорошими, средними и плохими в зависимости от вероятности попадания в цель. Введем в рассмотрение три гипотезы:

Н₁ - выбрано хорошее ружье;

Н₂ - выбрано среднее ружье;

Н₃ - выбрано плохое ружье.

Из условия по классическому определению вероятности получим, что P(Н₁)=5/10, P(Н₂)=3/10, P(Н₃)=2/10. Условные вероятности — это заданные в задаче числа(0.8, 0.6 и 0.3). Вероятность попадания в цель находим по формуле

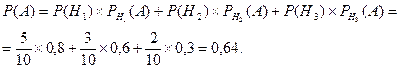
Задача 2. Имеются две урны с шарами: в первой 4 белых шара и 6 черных шаров, во второй - 4 белых и 2 черных. Из первой урны достают наугад два шара и перекладывают их во вторую урну. Затем из второй урны достают наугад один шар. Какова вероятность того, что он будет белым?

Решение. Рассмотрим три гипотезы:

Н₁ - из первой во вторую урну переложили два черных шара;

Н₂ - переложили два белых шара;

Н₃ - переложили белый и черный шары.

Общее число исходов при перекладывании шаров — 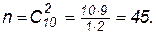Число исходов, благоприятствующих событиям Н₁, Н₂ и Н₃, равны, соответственно,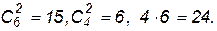

Отсюда по классическому определению находим вероятности гипотез:

р(Н₁)=15/45; р(Н₂)=6/45; р(Н₃)=24/45.

После перекладывания во второй урне окажется 8 шаров, но состав шаров в ней будет зависеть от того, какая из трех гипотез имела место. Обозначим через A событие, состоящее в том, что вынутый из второй урны шар окажется белым.

Если имела место гипотеза Н₁, то во второй урне - 4 белых шара и 4 черных. Поэтому

Если имела место гипотеза Н₂, то во второй урне - 6 белых шаров и 2 черных, т.е.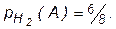

Если, наконец, имела место гипотеза Н₃, то во второй урне 5 белых шаров и 3 черных, т.е.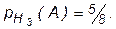

Таким образом, по формуле полной вероятности

Дата добавления: 2014-11-16