Сочетания

Сочетанием (без повторений) из n элементов множества A={a₁, a₂,..., a_n} по k называется любой неупорядоченный набор из k элементов множества А (0£k£n).

Следовательно каждое сочетание без повторений совпадает с подмножеством множества A.

Для любого сочетания из k элементов число различных размещений из этих же элементов равно числу перестановок Р_k. Поэтому

А_n^k =С_n^k× Р_k.

Следовательно,

С_n^k = А_n^k/ Р_k.

Таким образом, число всех сочетаний из n по k можно вычислить по формуле:

.

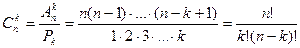Для числа С_n^k используют также обозначение .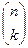

Рассмотрим более сложные задачи, которые решим, применяя классическое определение вероятности.

Задача 1. Бросают два кубика. Какова вероятность того, что сумма выпавших на них цифр окажется больше шести?

Решение. Элементарный исход данного испытания можно представить себе как пару чисел (i, j), где i - это цифра, выпавшая на первом кубике, j - на втором кубике. Следовательно, исходами являются размещения из 6 элементов по 2 с повторениями. Значит, можно найти число всех исходов:

n=6²=36;

Для подсчета числа благоприятных исходов удобно записать все исходы в виде таблицы:

(1, 1) (1, 2)... (1, 6)

(2, 1) (2, 2)... (2, 6)

(3, 1) (3, 1)... (3, 6)

...

(5, 1) (5, 2)... (5, 6)

(6, 1) (6, 2)... (6, 6)

Событию А (сумма цифр больше 6) благоприятствуют те исходы, которые расположены в таблице ниже проведенной над диагональю линии.

Таким образом,

m=1+2+3+4+5+6=21.

Следовательно, Р(А)=21/36=7/12.

Задача 2. Монету подбросили 5 раз. Найти вероятность того, что ровно один раз она упадет вверх “решкой”.

Решение. Любой исход данного испытания можно представить в виде пятибуквенного слова (с буквами О и Р). Например, исход ОРООР означает, что первый раз монета упала орлом, второй раз - решкой, третий раз - орлом, четвертый раз - орлом, пятый раз - решкой. Число всех таких слов вычисляется как число размещений из двух элементов по 5 с повторениями:

n=2⁵=32.

Указанному событию благоприятствует m=5 исходов, а именно:

РОООО, ОРООО, ООРОО, ОООРО, ООООР.

Поэтому: Р(А)=5/32.

Задача 3. Из колоды в 36 карт по очереди наугад достают три карты (назад карты не возвращаются). Найти вероятность того, что вторая по счету из них будет тузом, а две другие - нет.

Решение. Исходом данного испытания будет являться размещение из 36 элементов по 3 без повторений. Поэтому:

n=36 × 35 × 34.

Число благоприятных исходов можно подсчитать следующим образом: рассмотрим упорядоченную тройку карт, в которой первая карта - не туз, вторая - туз, третья - не туз. В этой тройке на первое место можно поставить любую из 32 карт (не тузов), на второе место - любого из 4 тузов, на третье место - любую из оставшихся 31 карты (не тузов). Значит, общее число таких троек будет равно:

m=32 × 4 × 31.

Таким образом,

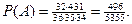
Задача 4. В закрытой урне находятся шары трех цветов: 5 белых, 3 черных и 2 красных. Из урны наугад достают три шара. Какова вероятность того, что они окажутся трех различных цветов.

Решение. Очевидно, что всевозможными исходами данного испытания являются сочетания из 10 элементов (общее число шаров в урне) по 3. Значит,

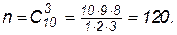
Число благоприятных исходов находим по правилу произведения:

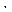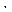m=5 3 2=30.

Следовательно,

Р(А)=30/120=1/4.

В некоторых задачах вычисление вероятности случайного события А непосредственно по классическому определению бывает сопряжено с довольно значительными вычислительными трудностями. В таких случаях обычно поступают следующим образом: рассматривают несколько более простых событий, через которые с помощью введенных ранее операций выражают данное событие А. Затем, используя те или иные формулы, сводят вычисление Р(А) к вероятностям этих более простых событий.

Рассмотрим теперь некоторые примеры применения формул сложения и умножения вероятностей.

Задача. 1. Наугад выбирают целое число N в пределах от 1 до 1000. Найти вероятность того, что число N делится либо на 3, либо на 5, либо на 7.

Решение. Рассмотрим три более простых события:

А₃ - число N делится на 3;

А₅ - число N делится на 5;

А₇ - число N делится на 7.

Очевидно, что рассматриваемое в задаче событие А=А₃+А₅+А₇. Поэтому по формуле сложения вероятностей:

р(А)=р(А₃+А₅+А₇)=р(А₃)+р(А₅)+р(А₇)-р(А₃А₅)-р(А₃А₇) - р(А₅А₇)+р(А₃А₅А₇)

Каждую из этих семи вероятностей легко найти по классическому определению, при этом общее число исходов n =1000, а число благоприятных исходов для каждого из семи событий получается в результате целочисленного деления числа n =1000 на 3, 5, 7, 15, 21, 35 и 105 соответственно. В результате получим:

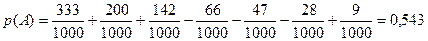
Задача 2. Найти вероятность того, что при шести бросаниях кубика выпадет хотя бы одна “шестерка”.

Решение. Рассмотрим следующие события:

А₁ - при первом бросании выпала “6”;

А₂ - при втором бросании выпала “6”;

...

А₆ - при шестом бросании выпала “6”.

Воспользуемся формулой:

р(А)= р(А₁+А₂+...+А₆)=1-р(`А<sub>1</sub>×А<sub>2</sub>×...`А₆).

Общее число всех исходов, а также число исходов, благоприятных для события (`А<sub>1</sub>×`А₂×...`А₆), найдем по правилу произведения:

n=6⁶, m=5⁶.

Таким образом, р(А)=1-5⁶/6⁶=30531/46656.

Значит: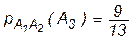

Задача 3. Имеется набор карточек, из которых 10 карточек с буквой М и 5 карточек c буквой А. Из этого набора не глядя берут 4 карточки и выкладывают их в ряд. Найти вероятность того, что получится слово МАМА.

Решение. Рассмотрим следующие события

А₁ - на первой карточке буква М;

А₂ - на второй карточке буква А;

А₃ - на третьей карточке буква М;

А₄ - на четвертой карточке буква А.

Очевидно, что нас интересует событие А₁А₂А₃А₄. По формуле умножения вероятностей (для зависимых событий):

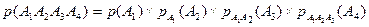
Каждую из этих четырех вероятностей найдем по классическому определению:

1. р(А₁)=10/15=2/5;

2. Предположим, что произошло событие А₁, а это значит, что среди оставшихся карточек 9 - с буквой М и 5 - с буквой А, поэтому: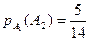

3. Предположим, что произошло событие А₁А₂, т.е. осталось 9 карточек с буквой М и 4 - с буквой А. Наконец, предположим, что произошло событие А₁А₂А₃, т.е. осталось 8 карточек с буквой М и 4 - с буквой А. Тогда: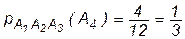

Таким образом,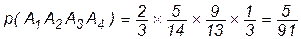

Задача 4. Вероятность попадания в цель для каждого из трех стрелков равны 0.8, 0.7 и 0.6 соответственно. Каждый из них выстрелил в цель по разу. Найти вероятность того, что по крайней мере двое из них попадут в цель.

Решение. Введем в рассмотрение три события:

А - первый стрелок попал в цель;

В - второй стрелок попал в цель;

С - третий стрелок попал в цель.

Интересующее нас событие выражается через А, В и С следующим образом:

АВС+`АВС+А`ВС+АВ`С,

причем слагаемые в этой сумме несовместны, а сомножители во всех произведениях независимы. Поэтому, используя формулы сложения и умножения вероятностей, а также вероятность противоположного события, получим вероятность требуемого события:

р=р(А)р(В)р(С)+р(`А)р(В)р(С)+р(А)р(`В)р(С)+р(А)р(В)р(`С)=

= 0.8×0.7×0.6+0.2×0.7×0.6+0.8×0.3×0.6+0.8×0.7×0.4=0,788.

Дата добавления: 2014-11-16