Биномиальное распределение

Определение случайной величины. Дискретные и непрерывные случайные величины. Функция распределения и ее свойства, плотность вероятностей непрерывной случайной величины.Биномиальное распределение. Распределение Пуассона.

Со многими испытаниями могут быть связаны не только какие-то случайные события, но также и случайные числа. Это может быть число очков на выпавших кубиках, число бракованных деталей в наугад выбранной партии, выигрыш (денежный) в некой игре и т.п. В связи с этим в теории вероятностей вводится понятие случайной величины.

Случайной величиной называется величина Х, которая в результате испытания может принимать единственное значение х, из заданных, наперед неизвестное.

Пусть {х₁, х₂, …, х_n} – конечный набор чисел (чаще всего в порядке возрастания). Дискретной случайной величиной (сокращенно, ДСВ) называется величина Х, которая в результате испытания может принимать одно из значений х_i, наперед неизвестное.

Законом распределения ДСВ Х называется таблица,

Х	х1	х2	х3	….	хn
Р	р1	р2	р3	….	рn

в верхней строке которой перечислены все возможные значения, которые может принимать Х, а в нижней – соответствующие им вероятности р_к=Р(Х=х_к) – вероятность того, что в результате испытания Х примет значение х_к. Заметим, что для закона распределения ДСВ Х всегда должно выполняться равенство:

Отметим также, что иногда приходится рассматривать ДСВ Х, возможные значения которой образуют бесконечное счетное множество

{х₁, х₂, …, х_n,…}, например, множество натуральных чисел.

Простейшим из законов распределения является равномерное распределение. Такой закон распределения характеризуется тем, что все вероятности р_к равны между собой, следовательно, он имеет вид:

Х	х1	х2	х3	….	хn
Р	1/n	1/n	1/n	….	1/n

Равномерное распределение получается, например, если рассмотреть ДСВ X - число очков, выпавших при бросании правильной игральной кости.

Последовательность независимых испытаний (схема Бернулли)

Рассмотрим некоторое испытание и связанное с ним случайное событие А. Пусть это испытание повторяется многократно при неизменных условиях. В таком случае говорят, что производится последовательность независимых испытаний (иногда это называется схемой Бернулли).

Примером является игра двух сторон на определенных условиях (бросание монеты или кубика, шахматы, карточные игры, лотереи, тотализаторы и т.п.), событие А – это выигрыш одной из сторон в данной игре. В схеме Бернулли принято событие А называть “успехом”, а противоположное ему событие `А – “неудачей”.

Предположим, что производится серия из n независимых испытаний с двумя исходами (“успех” или “неудача”) в каждом испытании; р – вероятность “успеха”; q=1-р – вероятность “неудачи” (обычно р и q либо заданы, либо легко вычисляются). Обозначим через k число успехов в этой серии, которое может принимать любые значения от 0 до n. Событие M_k, состоящее в том, что число успехов в нашей серии испытаний окажется равным именно числу k, является случайным. Его вероятность Р (M_k) (обозначают через Р_n(k)) может быть найдена по формуле Бернулли (Якоб Бернулли (1654 – 1705) – швейцарский математик):

P_n(k)=C^k_np^kq^n–k

(доказательство формулы Бернулли можно получить, используя формулы сложения и умножения вероятностей).

Рассмотрим некоторые примеры.

Задача 1. Монету бросают 10 раз. Найти вероятность того, что число выпавших “орлов” и “решек” будут одинаковым.

Решение. Пусть успех – это, например, выпадение орла при одном бросании, тогда р=q=1/2. Общее число испытаний n=10, число успехов k равно 5. Значит, по формуле Бернулли:

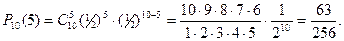
Задача 2. Кубик бросают 4 раза. Какова вероятность того, что не меньше двух раз выпадет цифра, большая четырех?

Решение. Будем понимать под успехом выпадение на кубике при одном бросании цифры, большей четырех (т.е. 5 или 6). Очевидно, вероятность успеха р=2/6=1/3; (q=2/3). Общее число испытаний n=4. Число успехов k должно быть равно 2, 3 или 4. Поэтому, применяя три раза формулу Бернулли, получим искомую вероятность

Задача 3. Вероятность попадания в цель при одном выстреле равна р=1/2. Известно, что для полного поражения цели требуется не менее трех попаданий. Какое минимальное количество выстрелов нужно произвести, чтобы с вероятностью не менее, чем 0.9, можно было утверждать, что цель поражена.

Решение. Предположим, что по цели произведено n выстрелов. Тогда вероятность поражения цели будет равна:

р_n(3)+р_n(4)+... +р_n(n)=1-p_n(0)-p_n(1)-p_n(2).

Минимальное число выстрелов, очевидно, определяется неравенством:

р_n(3)+р_n(4)+... +р_n(n)³0,9 или

р_n(0)+р_n(1)+р_n(2)£0,1.

Отсюда по формуле Бернулли:

Легко убедиться в том, что это неравенство будет выполняться, начиная с n=9. Таким образом, минимальное число выстрелов для поражения цели с вероятностью 0.9 будет равно 9.

Из рассмотренных примеров видно, что формулой Бернулли нетрудно пользоваться, если число испытаний n невелико. На практике же встречаются серии из нескольких десятков, сотен и даже тысяч испытаний. В таких случаях формула Бернулли практически непригодна и вместо нее используют приближенные формулы, о которых пойдет речь несколько позже.

Рассмотрим схему Бернулли (n – число всех испытаний; р – вероятность успеха в одном испытании; q=1-р – вероятность неудачи). Пусть случайная величина Х – это число успехов во всей серии. Для любого 0£k£n вероятность того, что Х в результате серии испытаний примет значение k вычисляется по формуле Бернулли:

P(X=k)=P_n(k)=C^k_np^kq^n–k

Полученный таким образом закон распределения и называется биномиальным:

Х	0	1	….	k	….	n
Р	Pn(0)	Pn(1)	….	Pn(k)	….	Pn(n)

Распределение Пуассона (Симеон Дени Пуассон (1781 – 1840) – французский математик)

Так называется закон распределения вида:

Х	0	1	2	….	k	….
Р	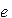^-^l	le^-^l

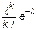
Можно показать, что распределение Пуассона является предельным случаем биномиального распределения, когда n – велико, р – мало, а l=n×p.

Пусть производится п независимых испытаний, в которых появление события А имеет вероятность р и число испытаний п достаточно велико (n >50), а вероятность появления события А в каждом испытании мала (p £0,1).

Сделаем важное допущение – произведение пр сохраняет постоянное значение:

l=n×p.

T.е, среднее число появления события в различных сериях из n испытаний остается неизменным.

По формуле Бернулли получаем:

,

подставим p = l/n:

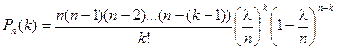
Найдем предел этой вероятности при п ®¥.

Получаем формулу распределения Пуассона:

.

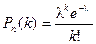Формула Пуассона дает по меньшей мере одну верную значащую цифру при n >50, p £0,1, 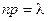<10.

Если известны числа l и k, то значения вероятности можно найти по таблицам распределения Пуассона.

Дата добавления: 2014-11-16