Основные определения

Тема 1.10. Сложное движение точки. Сложное движение твердого тела

ЛЕКЦИЯ 12

Тема 1.9. Кинематика. Простейшие движения твердого тела

Иметь представление о системах координат, об абсолютном, относительном и переносном движениях.

Знать разложение сложного движения на относительное и переносное, теорему сложения скоростей.

Знать разложение плоскопараллельного движения на поступа­тельное и вращательное, способы определения мгновенного центра скоростей.

Сложным движением считают движение, которое можно раз­ложить на несколько простых.

Простыми движениями считают

· по­ступательное и

· вращательное.

Для рассмотрения сложного движения точки выбирают две си­стемы отсчета:

· подвижную и

· неподвижную.

Движение точки (тела) относительно неподвижной системы от­счета называют сложным, или абсолютным.

Подвижную систему отсчета обычно связывают с движущимся телом. Движение подвижной системы отсчета относительно непо­движной называют переносным.

Движение материальной точки (тела) по отношению к подвиж­ной системе называют относительным.

Примером может служить движение человека по эскалатору метро. Движение эскалатора — переносное движение, движение че­ловека вниз или вверх по эскалатору — относительное, а движение по отношению к неподвижным стенам станции — сложное (абсолютное) движение.

При решении задач используют теорему о сложении скоростей:

При сложном движении точки абсолютная скорость в каж­дый момент времени равна геометрической сумме переносной (v_e) и относительной (v_r) скоростей:

α — угол между векторами v_e и v_r.

Плоскопараллельное движение твердого тела

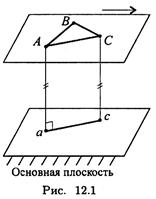Плоскопараллелъным, или плоским, называется такое движение твердого тела, при котором все точки тела перемещаются параллель­но некоторой неподвижной в рассматриваемой системе отсчета плос­кости.

Плоскопараллельное движение мож­но изучать, рассматривая любое плоское сечение тела, параллельное неподвижной плоскости, называемой основной (рис. 12.1).

Все точки тела, расположенные на прямой, перпендикулярной к основной плоскости, движутся одинаково.

Плоскопараллельное движение изуча­ется двумя методами: методом разложения сложного движения на поступательное и вращательное и методом мгновенных центров скоростей.

Метод разложения сложного движения на поступа­тельное и вращательное

Плоскопараллельное движение раскладывают на два движения: поступательное вместе с некоторым полюсом и вращательное отно­сительно этого полюса.

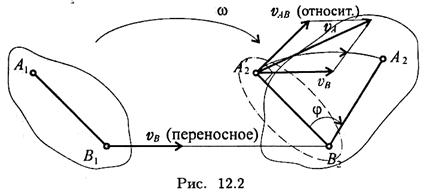Разложение используют для определения скорости любой точки тела, применяя теорему о сложении скоростей (рис. 12.2).

Точка А движется вместе с точкой В, а затем поворачивается вокруг В с угловой скоростью и, тогда абсолютная скорость точки А будет равна

v_A = v_B + v_AB, v _{A B} = ωr (r = АВ).

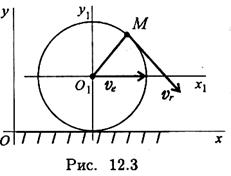Примером плоскопараллельного движения может быть движе­ние колеса на прямолинейном участке дороги (рис. 12.3).

Скорость точки М

v_M = v_e + v_r,

v_e — скорость центра колеса переносная; v_r — скорость вокруг центра относитель­ная.

уОх — неподвижная система координат,

y₁0₁x₁ — подвижная система координат, связанная с осью колеса.

Дата добавления: 2014-11-16