Тема. Вычисление неопределенных интегралов

Практическое занятие №8

Подведение итогов работы на занятии. Работу можно закончить дома.

Цель:

-обобщить и систематизировать: понятие интеграла, таблицу интегралов, методы вычисления интегралов

- получить практический навык нахождения интегралов путем непосредственного интегрирования, методом замены переменной, методом интегрирования по частям

Ход занятия

Неопределённый интеграл и таблица неопределённых интегралов

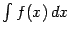Определение Пусть -- функция, заданная на объединении интервалов вещественной оси. Набор всех первообразных для называется неопределённым интегралом от и обозначается . Операция нахождения неопределённого интеграла по заданной функции называется интегрированием этой функции; найти неопределённый интеграл означает проинтегрировать данную функцию. Функция , записанная после знака интеграла (или, как часто говорят, под знаком интеграла), называется подынтегральной функцией.

Согласно доказанным выше теоремам о виде первообразных, неопределённый интеграл от функции состоит из функций вида 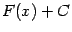, где 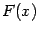-- какая-либо фиксированная первообразная для , а -- величина, постоянная на каждом из непересекающихся интервалов, на которых задана функция . Поэтому можно написать такую формулу:

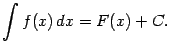
(Точнее было бы , но фигурные скобки, обозначающие множество всех функций вида 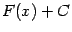, писать в данной ситуации не принято.)

Итак, для того чтобы доказать равенство , достаточно проверить, что 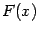-- первообразная для , то есть что .

	.		.
	.		.
	().		.
	.		.
	; .		.
	.
	.		.
	.		.
	.		.
	.		; .

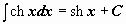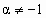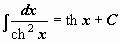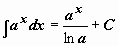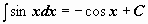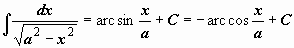
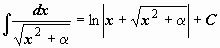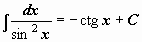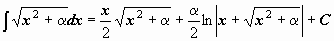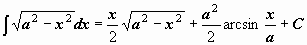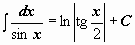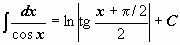Интегрирование по частям.

Интегрирование по частям - приём, который применяется почти так же часто, как и замена переменной. Пусть u(x) и v(x) - функции, имеющие непрерывные частные производные. Тогда по формуле дифференцирования произведения d(uv) = u∙dv + v∙du . Находим неопределённые интегралы для обеих частей этого равенства (при этом ):
.
Эта формула и называется формулой интегрирования по частям. Часто ее записывают в производных (dv = v’∙dx, du = u’∙dx):

.

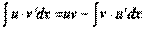Примеры:
. .
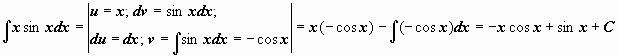Формула интегрирования по частям может применяться неоднократно. При наличии небольшого опыта в простых интегралах нет необходимости выписывать промежуточные выкладки (u = …, dv = …), можно сразу применять формулу, представив интеграл в виде : .

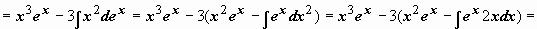
Приведённые примеры показывают, для каких функций надо применять (или попытаться применить) формулу интегрирования по частям:
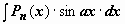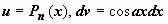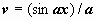Интегралы вида , , , где Pn(x) - многочлен n-ой степени. Так, для имеем , , и 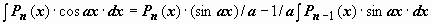. В результате мы получили интеграл того же типа с многочленом степени на единицу меньше. После n-кратного применения формулы степень многочлена уменьшится до нуля, т.е. многочлен превратится в постоянную, и интеграл сведётся к табличному.
Интегралы 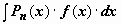, где 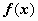- трансцендентная функция, имеющая дробно-рациональную или дробно-иррациональную производную (ln x, arctg x, arcctg x, arcsin x, arcos x). В этом случае имеет смысл взять u = f(x), dv = Pn(x)dx, для того, чтобы в интеграле 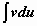участвовала не f(x), а её производная. Пример: .

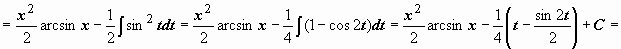
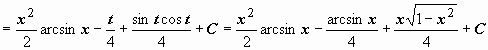Замена переменной в неопределённом интеграле
(интегрирование подстановкой).

Пусть 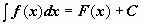. Тогда . Здесь t(x) - дифференцируемая монотонная функция.
При решении задач замену переменной можно выполнить двумя способами.
1. Если в подынтегральной функции удаётся сразу заметить оба сомножителя, и f(t(x)), и 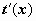, то замена переменной осуществляется подведением множителя 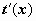под знак дифференциала: , и задача сводится к вычислению интеграла 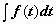. Например, (задача сведена к вычислению , где t = cos x) (аналогично находится интеграл от ); 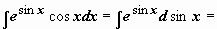(задача сведена к вычислению 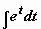, где t = sin x) 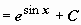. В более сложных задачах операция подведения под знак дифференциала может выполняться несколько раз: (самое неприятное в подынтегральной функции - пятая степень арккотангенса под знаком экспоненты; если дальше не найдётся дифференциал этой функции, то интеграл, возможно, взять вообще не удастся; в то же время следующий множитель (arcctg4 x2) - производная (с точностью до постоянного множителя) степенной функции; затем следуют производные (опять с точностью до постоянных множителей) функций arcctg x2 и x2 по своим аргументам)

.

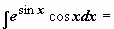
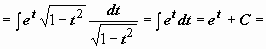2. Замену переменной можно осуществлять формальным сведением подынтегрального выражения к новой переменной. Так, в имеет смысл перейти к переменной (сделать подстановку) t = sin x. Выражаем все множители подынтегрального выражения через переменную t: ; в результате (возвращаемся к исходной переменной) 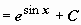. Другие примеры:
. Подынтегральная функция содержит два множителя, ни один из которых не является производной другого, поэтому подводить их под знак дифференциала бесполезно. Попытаемся ввести новую переменную, такую, чтобы корни извлеклись: = 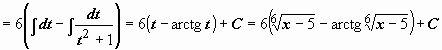. Рассмотрим (интеграл №19 из табл.). Здесь подынтегральная функция состоит из единственного множителя; можно опять попытаться сделать такую замену переменной, чтобы корень извлёкся. Структура подкоренного выражения подсказывает эту замену: 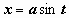(или , ): . 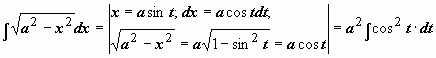Интеграл свёлся к интегралу от квадрата косинуса. При интегрировании чётных степеней синуса и косинуса часто применяются формулы, выражающие 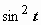и 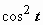через косинус двойного угла: . Поэтому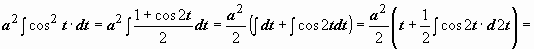
.
Примеры: 1.

.

2.

.

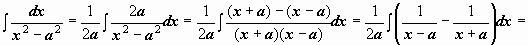
Вариант 1. Вычислить интегралы:

непосредственным интегрированием 1-3

методом замены переменной 4-6

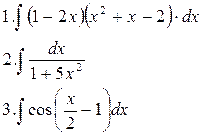
Вариант 2. Вычислить интегралы:

непосредственным интегрированием 1-3

методом замены переменной 4-6

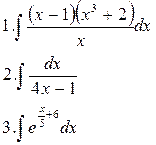
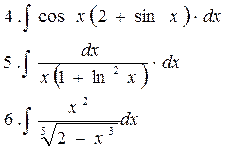
Вариант 3. Вычислить интегралы:

непосредственным интегрированием 1-3

методом замены переменной 4-6

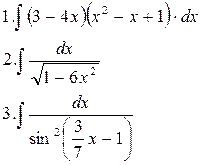
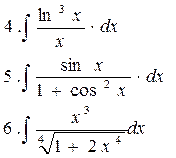
Дата добавления: 2014-11-16