Основные формулы

ЗАДАЧИ

1. Первую треть пути между пунктами велосипедист проехал со скоростью v = 5 м/с. Затем половину оставшегося времени он ехал со скоростью v = 10 м/с, после чего до конечного пункта он шел пешком со скоростью v = 1 м/с. Определить среднюю скорость движения велосипедиста.

[5,3 м/с].

2. Найти среднюю скорость тела в двух случаях: а) первую четверть времени оно двигалось со скоростью v = 5 м/с, вторую четверть времени - со скоростью v = 10 м/с, оставшуюся часть времени со скоростью v = 15 м/с: б) первую четверть пути оно двигалось со скоростью v = 5 м/с, вторую четверть пути со скоростью v = 10 м/с, оставшуюся часть пути - со скоростью v = 15 м/с.

[11,25 м/с; 9,2 м/с].

3. Зависимость пройденного телом пути S от времени t дается уравнением S = At +Bt ² +Ct ³ , где A = 2 м/c, B = 3м/с²,
С = 4 м/с³. Найти: а) зависимость скорости v и ускорения a от времени t; б) расстояние S, скорость v, ускорение a через время
t = 2 с после начала движения; в) среднюю скорость и среднее ускорение за это время.

[б) 48 м; 62 м/с; 54 м/с². в) 24 м/с; 30 м/с²].

4. С балкона небоскреба высотой 100 м бросили мяч. Через какое время мяч упадет на землю, если начальная скорость мяча v _o равна: а) 0; б) 5 м/с и направлена вверх; в) 5 м/с и направлена вниз?

[4,5 с; 5,1 с; 4,0 с].

5. Свободно падающее тело в последнюю секунду своего движения прошло половину пути. С какой высоты падало тело, и каково время его падения?

[3,4 с; 56,6 м].

6. С башни высотой 20 м горизонтально брошен камень со скоростью v ₀ = 10 м/с. Какое время камень будет находиться в движении? На каком расстоянии от башни он упадет на землю?
С какой скоростью он упадет на землю? Какой угол с горизонтом составит траектория камня в точке его падения на землю?

[2,0 с; 20,0 м; 22,0 м/с; 63,0^о ].

7. Камень брошен горизонтально с начальной скоростью 10 м/с. Найти скорость камня, нормальное и тангенциальное ускорение через 2 с и радиус кривизны траектории в этот момент.

[22,0 м/с; 4,5 м/с²; 8,7 м/с²; 107,6 м].

8. Тело брошено под углом 30^о к горизонту с начальной скоростью 10 м/с. Найти зависимость координат, а также горизонтальной и вертикальной составляющих скорости от времени. Определить уравнение траектории движения, максимальную высоту и время подъёма, время полета и дальность полета.

[ 1,3 м; 0,5 с; 1,0 с; 8,5 м].

9. Мяч брошен со скоростью v = 10 м/с под углом a =45^o к горизонту. На какую высоту h поднимется мяч? На каком расстоянии l от места бросания он упадет на землю? Какое время t он будет в движении? Определить скорость, ускорение и радиус кривизны в 2-х любых точках траектории.

[2,4 м; 10,0 м; 1,4 с].

10. С башни высотой h = 25 м брошен камень со скоростью
v = 15 м/с под углом a = 30^о к горизонту. Какое время t камень будет в движении? На каком расстоянии l от основания башни он упадет на землю? С какой скоростью он упадет на землю? Какой угол j составит траектория камня с горизонтом в точке падения? Определить нормальное, тангенциальное ускорения и радиус кривизны траектории в точке соприкосновения камня с землей?

[ 3,2 с; 41,1 м; 26,7 м/с; 61^о; 4,7 м/с²; 8,5 м/с²; 151,7 м].

11. Точка движется по окружности радиусом R = 0,2 м. Зависимость пути от времени дается уравнением S = Ct ³, где
C = 0,1 м/с³. Найти нормальное a _н, тангенциальное a _ти полное ускорение точки, когда ее линейная скорость v = 2 м/с. Чему равны в этот момент ее угловая скорость и угловое ускорение?

[ 20 м/с²; 1,55 м/с²; 20,06 м/с²;10 рад/с; 7,8 рад/с²].

12. Точка движется по окружности радиусом R = 0,1 м с постоянным тангенциальным ускорением. Найти ускорение точки через 10 с после начала движения, если известно, что к концу пятого оборота после начала движения линейная скорость точки
v = 0,8 м/с.

[а_t = 0,1 м/с²; а_n = 10,0 м/с²; а = 10,0 м/с²].

13. Колесо, вращаясь равноускоренно, достигло угловой скорости w = 20 рад/с, сделав 10 оборотов после начала вращения. Найти угловое ускорение колеса. Какое число оборотов сделает колесо за 2 с в промежутке между 8-й и 10-й секундами? Какую угловую скорость оно будет иметь в эти моменты времени? Чему будет равна средняя угловая скорость в этот промежуток времени и как она связана с числом оборотов?

[3,2 рад/с²; 25,6 рад/с; 32 рад/с;28,8 рад/с; 9,2 об.]

14. Вентилятор вращается с частотой n = 900 об/мин. После выключения электродвигателя, вращаясь равно замедленно, он сделал до остановки N = 75 оборотов. Через какое время после выключения из сети вентилятор остановится? Какую скорость он имел в середине этого временного промежутка?

[10 с; 47,1 рад/с].

15. Найти угловое ускорение колеса, если известно, что через время t = 2 с после начала движения вектор полного ускорения точки, лежащей на ободе, составляет угол a = 60^о с вектором ее линейной скорости?

[0,43 рад/с²].

16. Во сколько раз нормальное ускорение a _н точки, лежащей на ободе вращающегося колеса, больше её тангенциального ускорения a _т в тот момент времени, когда вектор полного ускорения точки составляет угол в 30^o с вектором её линейной скорости?

[ а _н / a _т = 0,6]

17. Из точки А, лежащей на верхнем конце вертикального диаметра некоторой окружности, по желобу, установленному вдоль различных хорд этой окружности, одновременно начинают скользить грузы. Через какое время грузы достигнут окружности? Как это время зависит от угла α? Трением пренебречь.

[ t ₁ = t ₂ = ].

18. Небольшое тело скользит со скоростью v = 10 м/с по горизонтальной плоскости, приближаясь к щели. Щель образована двумя отвесными стенами, находящимися на расстоянии d = 5 см друг от друга. Глубина щели h = 1 м. Сколько раз тело ударится о стенки, прежде чем упадет на дно? Удар считать абсолютно упругим.

[ N = 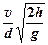= 90].

19. Гладкий диск радиуса R, плоскость которого горизонтальна, вращается вокруг своей оси с частотой n = 40 об/мин. От поверхности на расстоянии R /2 от оси вращения отрывается небольшое тело, которое без трения скользит по диску. Через какое время оно соскользнет с диска?

[ t = = 0,41 c].

20. Колесо радиуса R равномерно катится по горизонтальной поверхности. От точки А на горизонтальном диаметре обода колеса отрывается капелька грязи. С какой скоростью движется колесо, если капелька, побывав в воздухе, снова опустилась на тоже самое место колеса? Сопротивление воздуха не учитывать.

[ v = 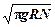, где N - число оборотов, сделанное колесом].

21. Шарик вертикально падает на наклонную плоскость, с углом наклона к горизонту a = 30^о. Пролетев расстояние h = 1 м, он упруго отскакивает от плоскости, и второй раз падает на нее же. Найти расстояние S между первым и вторым ударами шарика о плоскость.

[ S = 8hsina = 4 м ].

Глава 2. Динамика материальной точки

Контрольные вопросы

1. Как называется главная научная работа И.Ньютона по механике, и когда она была опубликована?

2. Сформулируйте закон инерции.

3. Какая система отсчета называется инерциальной и как установить ее инерциальность?

4. Что такое сила? Как найти результирующую системы сил?

5. Сформулируйте и запишите в векторной форме 2-ой закон Ньютона.

6. Что такое сила тяжести и вес? Как они связаны между собой?

7. Сформулируйте и запишите закон всемирного тяготения.

8. Какие четыре типа взаимодействий знает физика? Какие взаимодействия изучаются в механике?

9. Что Вы знаете о силе трения?

10. Запишите закон Гука для упругих деформаций растяжения и сдвига.

11. Что такое система материальных точек? Как найти ее импульс? Сформулируйте закон сохранения импульса и приведите примеры его проявления.

12. Что такое центр масс двух материальных точек? Как найти координаты центра масс системы материальных точек?

13. Сформулируйте законы движения центра масс.

14. Сформулируйте принцип относительности Галилея.

15. Сформулируйте постулаты СТО и назовите главные следствия из них.

Импульс материальной точки массой m, движущейся со скоростью ,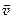

.

Второй закон Ньютона

.

где 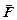– результирующая сила, действующая на материальную точку.

При небольших скоростях: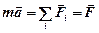

Силы, рассматриваемые в механике:

а) сила тяжести

;

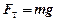б) сила гравитационного взаимодействия

,

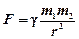где g – гравитационная постоянная; m ₁ и m₂ – массы взаимодействующих тел; r – расстояние между телами (тела рассматриваются как материальные точки);

в) сила упругости

,

где k – коэффициент упругости (в случае пружины – жесткость); х – абсолютная деформация;

г) Сила трения скольжения

,

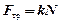где k - коэффициент трения скольжения, N - сила реакции опоры.

Закон сохранения импульса:

импульс замкнутой системы материальных точек есть величина постоянная (или – импульс тел до взаимодействия равен их импульсу после взаимодействия).

.

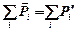Дата добавления: 2014-11-16