Методические указания. 1. После краткой записи условия задачи сделать чертеж и указать на нем все силы, действующие на тела системы

1. После краткой записи условия задачи сделать чертеж и указать на нем все силы, действующие на тела системы, все моменты сил и все векторные кинематические характеристики движения.

2. Записать второй закон Ньютона для вращательного движения 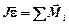. Так как в курсе общей физики обычно рассматривается вращение твердого тела лишь вокруг неподвижной оси (или оси, перемещающейся в пространстве параллельно самой себе), то на нее и проектируют векторное уравнение. В этом случае все векторы, характеризующие вращательное движение тела: 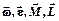, направлены вдоль оси вращения.

3. Для тел, движущихся поступательно, записывают второй закон Ньютона в форме 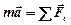и проектируют его на выбранные оси координат (обычно на одну ось).

4. Используя кинематические связи между телами и соотношения между линейными и угловыми характеристиками, упрощают записанные уравнения и добиваются, чтобы их число было равно числу неизвестных. Решая их, находят искомые величины.

5. Закон сохранения механической энергии, при решении задач на вращательное движение, применяется особенно в тех случаях, когда законы вращения сложны или даже неизвестны. Следует помнить, что полная кинетическая энергия твердого тела складывается из кинетической энергии его поступательного движения со скоростью центра масс и кинетической энергии вращения вокруг оси, проходящей через центр масс.

6. Закон сохранения момента импульса при вращательном движении, как и закон сохранения импульса при поступательном движении, позволяет исключить из рассмотрения внутренние силы. Этот закон справедлив для системы, если она замкнута или результирующий момент всех внешних сил, действующих на систему, равен нулю.

ЗАДАЧИ

66. К ободу однородного диска радиусом 0,2 м приложена касательная сила 98,1 H. При вращении на диск действует момент сил трения 4,9 Н×м. Найти массу диска, если известно, что диск вращается с угловым ускорением 100 рад/с².

[7,36 кг]

67. Однородный диск радиусом 0,2 м и массой 5 кг вращается вокруг оси, проходящей через его центр перпендикулярно к его плоскости. Зависимость угловой скорости вращения диска от времени дается уравнением w = A +Вt, где В = 8 рад/с². Найти касательную силу F, приложенную к ободу диска. Трением пренебречь.

[4,0 Н]

68. Маховик, момент инерции которого 63,6 кг×м², вращается с угловой скоростью 31,4 рад/с. Найти момент сил торможения, под действием которого маховик останавливается через 20 с. Маховик считать однородным диском.

[100 Н×м]

69. К ободу колеса, радиусом 0,5 м и массой 50 кг, приложена касательная сила 98,1 Н. Найти угловое ускорение колеса. Через какое время после начала действия силы колесо будет иметь частоту вращения в 100 об/с? Колесо считать однородным диском. Трением пренебречь.

[7,8 рад/с²; 80 с]

70. Маховое колесо, момент инерции которого 245 кг×м², вращается с частотой 20 об/с. Через 1 минуту после того, как на колесо перестал действовать момент сил, оно остановилось. Найти момент сил трения и число оборотов, которое сделало колесо до полной остановки после прекращения действия сил. Колесо считать однородным диском.

[513 Н×м; 600 об.]

71. Две гири с массой 2 кг и 1 кг соединены нитью, перекинутой через блок массой 1 кг. Найти ускорение, с которым движутся гири, и силы натяжения нитей, к которым подвешены гири. Блок считать однородным диском. Трением пренебречь.

[2,8 м/с²; 14 Н; 12,6 Н]

72. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого 50 кг×м² и радиус 20 см. Момент сил трения вращающегося блока 98,1 Н×м. Найти разность натяжения нити по обе стороны блока, если известно, что блок вращается с угловым ускорением 2,36 рад/с². Блок считать однородным диском.

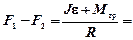[ 1,08 кН]

73. Блок массой 1 кг укреплен на конце стола. Гири 1 и 2 одинаковой массы по 1 кг соединены нитью, перекинутой через блок. Коэффициент трения гири 2 о стол k = 0,1. Найти ускорение, с которым движутся гири, и силы натяжения нитей. Блок считать однородным диском. Трением в блоке пренебречь.

[3,53 м/с²; 6,3 Н; 4,5 Н]

74. Диск массой 2 кг катится без скольжения по горизонтальной плоскости со скоростью 4 м/с. Найти кинетическую энергию диска.

[24 Дж]

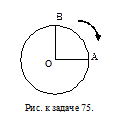
75. Обруч радиуса r скатился без проскальзывания с горки высотой h. Найти скорости и ускорения точек A и B обода. (А - наивысшая точка обода, В - находится на 1/4 окружности по направлению вращения).

[ ; ; ]

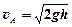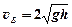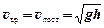76. На вертикальной оси укреплена горизонтальная штанга, по которой могут свободно перемещаться два груза с массами m ₁ и m ₂, связанные нитью длины l. Система вращается с угловой скоростью w. На каких расстояниях от оси будут находиться грузы в равновесии? Чему равны при этом сила натяжения нити и кинетическая энергия грузов? Вернутся ли грузы в положение равновесия, если их сместить из этого положения на малое расстояние?

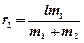[ ; ; равновесие неустойчивое;

; ]

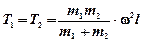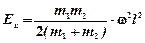77. Шар диаметром 6 см и массой 0,25 кг катится без скольжения по горизонтальной плоскости с частотой вращения 4 об/с. Найти кинетическую энергию шара.

[ E _к= 0,1 Дж]

78. Диск диаметром 60 см и массой 1 кг вращается вокруг своей оси, проходящей через центр перпендикулярно к его плоскости, с частотой 20 об/с. Какую работу А надо совершить, чтобы остановить диск?

[ А = -355 Дж]

79. Кинетическая энергия вала, вращающегося с частотой 5 об/с, равна 60 Дж. Найти момент импульса L вала.

[ L = 3,8 кг×м²/с]

80. Найти кинетическую энергию велосипедиста, едущего со скоростью 9 км/ч. Масса велосипедиста вместе с велосипедом 78 кг, причем на колеса приходится масса 3 кг. Колеса велосипеда считать обручами.

[ Е _к = 253 Дж]

81. Мальчик катит обруч по горизонтальной дороге со скоростью 7,2 км/ч. На какое расстояние может вкатиться обруч на горку за счет его кинетической энергии? Уклон горки равен 10 м на каждые 100 м пути.

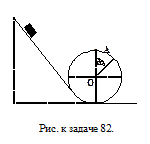[ S = 4,1 м]

82. Тело массой m совершает мертвую петлю, соскальзывая с минимально необходимой для этого высоты. С какой силой тело давит на опору в точке А, радиус-вектор которой составляет угол a с вертикалью? Трением пренебречь.

[ F _н = 3mg(1- cos a) ]

83. С какой наименьшей высоты должен съехать велосипедист, чтобы по инерции (без трения) проехать дорожку, имеющую форму «мертвой петли» радиусом 3 м, и не оторваться от дорожки в верхней точке петли? Масса m велосипедиста вместе с велосипедом 75 кг, причем на колеса приходится масса m_o = 3 кг. Колеса велосипеда считать обручами.

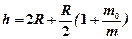[ = 7,56 м ]

84. Автомобиль массой 1000 кг движется со скоростью 36 км/ч по выпуклому мосту, имеющему радиус кривизны 50 м. С какой силой давит автомобиль на мост в середине? С какой минимальной скоростью должен двигаться автомобиль для того, чтобы в верхней точке он перестал оказывать давление на мост?

[7,8 кН; ~ 80км/ч ]

85. Автомобиль массой 2000 кг движется со скоростью 36 км/ч по вогнутому мосту, имеющему радиус кривизны 100 м. С какой силой давит автомобиль на мост в середине?

[21,6 кН]

86. Найти линейные скорости движения центров масс шара, диска и обруча, скатывающихся без скольжения с наклонной плоскости. Высота наклонной плоскости 0,5 м, начальная скорость всех тел равна нулю. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения.

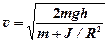[ ; v ₁ = 2,65 м/с; v ₂ = 2,56 м/с; v ₃ = 2,21 м/с; =3,13 м/с ]

87. Колесо, вращаясь равнозамедленно, уменьшило за 1 мин частоту вращения от 300 об/мин до 180 об/мин. Момент инерции колеса равен 2 кг×м². Найти угловое ускорение колеса, момент сил торможения, работу сил торможения и число оборотов, сделанных колесом за 1 мин.

[ e = - 0,21 рад/с²; M = - 0,42 Н×м; A = - 630 Дж; N = 240 об.]

88. Однородный стержень длиной 85 см подвешен к горизонтальной оси, проходящей через верхний конец стержня. Какую скорость надо сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси?

[ v = 7,1 м/с ]

89. Горизонтальная платформа массой 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой 10 об/мин. Человек массой 60 кг стоит при этом на краю платформы. С какой частотой начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека - точечной массой.

[ n ₂ = 22 об/мин ]

90. Горизонтальная платформа массой 80 кг и радиусом 1 м вращается с частотой 20 об/мин. В центре платформы стоит человек и держит в расставленных руках гири. С какой частотой будет вращаться платформа, если человек, опустив руки, уменьшит свой момент инерции от 2,94 до 0,98 кг×м ²? Считать платформу однородным диском.

[ n ₂ = 21 об/мин ]

91. Человек массой 60 кг находится на неподвижной платформе массой 100 кг. С какой частотой будет вращаться платформа, если человек будет двигаться по окружности радиусом 5 м вокруг оси вращения? Скорость движения человека относительно платформы 4 км/ч. Радиус платформы 10 м. Считать платформу однородным диском, а человека - точечной массой.

[ n = 0,49 об/мин]

Глава 5. Механические колебания и волны

Контрольные вопросы

1. Какое движение называют колебаниями?

2. Какие колебания называются гармоническими? Какими величинами они характеризуются?

3. Как найти скорость и ускорение колеблющейся точки в любой момент времени? Покажите на конкретном примере.

4. Запишите второй закон Ньютона для гармонически колеблющейся материальной точки.

5. Как найти кинетическую и потенциальную энергию гармонических колебаний материальной точки?

6. Вспомните формулы периодов колебаний математического, пружинного и физического маятников.

7. Какое движение получается при сложении двух гармонических одинаково направленных колебаний с одинаковыми частотами? Каковы будут характеристики этого движения?

8. Когда возникают биения? Напишите уравнения биений и охарактеризуйте величины, входящие в него.

9. Какова будет траектория результирующего колебания при сложении двух взаимно перпендикулярных гармонических колебаний с одинаковыми частотами?

10. Какие колебания называются затухающими? Напишите уравнение затухающих колебаний и поясните его.

11. Что такое время релаксации? Как оно связано с показателем затухания?

12. Что называется логарифмическим декрементом затухания? Каков его физический смысл?

13. Какие колебания называются вынужденными? Проанализируйте зависимость амплитуды вынужденных колебаний от соотношения частоты вынуждающей силы и собственной частоты системы.

14. Выведите уравнение плоской бегущей волны.

15. Когда при наложении когерентных волн происходит усиление колебаний, а когда ослабление?

16. Каков физический смысл вектора Умова? Чему равна его величина и как он направлен?

17. Какие волны называют стоячими? Как их можно получить? Запишите уравнение стоячей волны и дайте необходимые пояснения.

Дата добавления: 2014-11-16