Основные формулы. Уравнение гармонических колебаний

Уравнение гармонических колебаний

,

где x - смещение точки от положения равновесия, А - амплитуда колебаний, w - циклическая частота, j ₀ - начальная фаза.

Циклическая частота связана с периодом и линейной частотой следующими соотношениями

.

Скорость и ускорение точки, совершающей колебание, определяются как первая и вторая производные от смещения по времени.

Сила, под действием которой точка массой m совершает гармонические колебания, определяется по 2 закону Ньютона

,

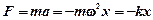где k - коэффициент возвращающей (квазиупругой) силы.

Кинетическая и потенциальная энергия колеблющейся точки:

,

.

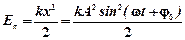Периоды колебаний простейших колебательных систем:

а) Математический маятник:

.

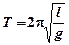б) Пружинный маятник:

.

в) Физический маятник

,

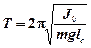где J _o - момент инерции маятника относительно его оси вращения, m - его масса, l_c - расстояние от центра масс до оси вращения, g - ускорение свободного падения.

При сложении двух одинаково направленных гармонических колебаний одинакового периода получается гармоническое колебание того же периода с амплитудой

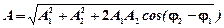
и с начальной фазой, определяемой из уравнения

,

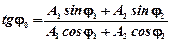где A ₁ и A ₂ - амплитуды складываемых колебаний, j₁ и j₂ -их начальные фазы.

При сложении двух взаимно перпендикулярных колебаний одинакового периода уравнение траектории результирующего движения имеет вид

.

Уравнение затухающих колебаний

,

где A ₀ e^{- b t} - амплитуда колебаний в данный момент времени t, A ₀ - амплитуда в начальный момент времени, 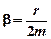- коэффициент (показатель) затухания, e - основание натуральных логарифмов, 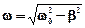- циклическая частота затухающих колебаний.

Логарифмический декремент затухания:

.

При распространении незатухающих колебаний со скоростью v вдоль оси х, смещение любой точки, отстоящей от источника колебаний на расстоянии l, дается уравнением (уравнение плоской бегущей волны)

,

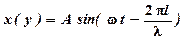где l = vT = v/n - длина волны, х - смещение для продольных колебаний, у - для поперечных.

Дата добавления: 2014-11-16