Теорема Лагранжа

Дифференциал ф-ции и его геометрический смысл. Св-ва дифференциала.

Производные 1,2-го порядка неявных ф-ций.

Производная высших порядков ф-ции 1й переменной.

y=f(x)

y``=(y`)`=lim((f`(x+Dx)-f`(x))/Dx)

x®0

y```=(y``)`= lim((f``(x+Dx)-f``(x))/Dx)

f⁽ⁿ⁾(x)=[f^(n-1)(x)]`

Неявной называется такая ф-ция у аргумента х, если она задана уравнением F(x,y)=0, не разрешенным относительно независимой переменной.

y=f(x), y=x²-1 - явные

F(x,y)=0, a²=x²+y² - неявные ф-ции.

1)a²=x²+y² - найдем производную, продифференцируем, считая у - сложной ф-цией х.

y`=2x+2y=0, т.к. а- постоянная

y*y`=-x, y`=-x/y

2) x³-3xy+y³=0

3x³-3(xy)`+3y<sup>2</sup>*y`=0 //:3

x²-(x`y+y`x)+y²*y`=0

y`y<sup>2</sup>-xy`=y-x²

y`=(y-x²)/(y²-x)

limy=A, y=A+a

limDy/Dx=y`, Dy/Dx=y`+a, Dy=y`Dx+aDx

Dx®0

Dy=y`Dx+e, где e-б.м.в., величина более высокого порядка малости,, чем Dx(a), и ее можно отбросить.

dy=y`Dx

Дифференциалом ф-ции наз. величина, пропорциональная б.м. приращению аргумента Dх и отличающаяся от соответствующего приращения ф-ции на б.м.в. более высокого порядка малости, чем Dх.

Если y=x, то dy=dx=x`Dx=Dx, dx=Dx

Если y¹x, то dy=y`dx, y`=dy,dx

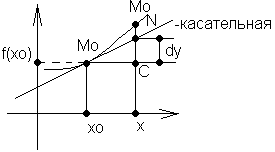
Геометрический смысл: дифференциал - изменение ординаты касательной, проведенной к графику ф-ции в точке (x₀,f(x₀)) при изменении x₀ на величину Dx

Св-ва:
1. (U±V)`=U`±V`, то (U±V)`dx=U`dx±V`dx, d(U±V)=d(U±V)

2. (UV)`=U`V+V`U, то (UV)`dx=V`dU+U`dV

3.d(c)=c`dx=0*dx=0

4. d(U/V)`=(V`dU-U`dV)/V².

Если функция f(x) непрерывна на [a,b] и дефференцирована на (a,b), то сущест.

т. с(a,b), такая, что: f(b)-f(a)=f’(c)(b-a).

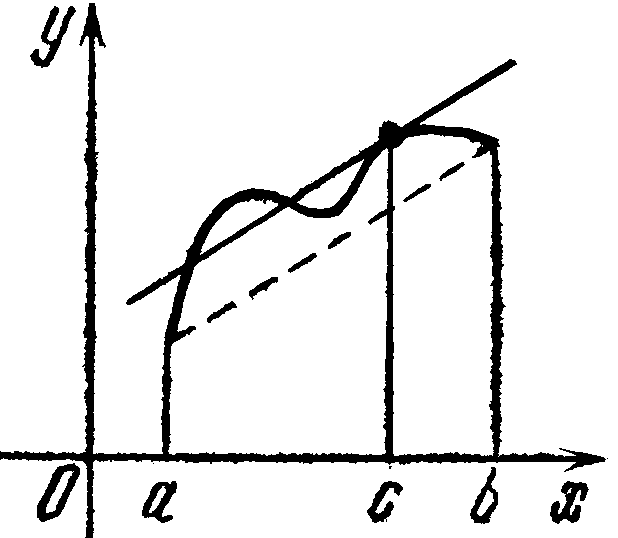Доказательство: Теорема Лагранжа имеет простой геометрический.смысл, если записать её в виде (f(b)–f(a))/(b–a)=f'(c)при(а<с<b). Левая часть этого равенства есть тангенс угла наклона к оси х хорды, стягивающей точки (a,f(a)) и (b,f(b)) графика функции y=f(x), а правая часть есть тангенс угла наклона касательной к графику в некоторой промежуточной точке с абсциссой сÎ(а,b). Теорема Лагранжа утверждает, что если кривая (рис) есть график непрерывной на [ а,b] функции, имеющей производную на (а,b), то на этой кривой существует точка, соответствующая некоторой абсциссе с(а<с<b) такая, что касательная к кривой в этой точке параллельна хорде, стягивающей концы кривой (a,f(a)) и (b,f(b)). Равенство {1} наз. формулой (Лагранжа) конеч­ных приращений. Промежуточное значение с удобно запи­сывать в виде c=a+q(b– a), где q есть некоторое число, удовлетворяющее неравенствам 0<q<1. Тогда формула Лагранжа примет видf(b)–f(a)=(b- a)f'(a +q(b–a)) (0<q<1). {2} Она верна, очевидно, не только для a <b, но и для a ³b.

Дата добавления: 2014-11-16