Основные приемы нахождения пределов

Й, 2й замечательный пределы.

Основные теоремы о пределах.

1. Предел суммы = суммы пределов:
limx=a, limy=b, тогда x=a+a, y=b+b, где a и b - б.м.в. x+y=(a+a)+(b+b)=(a+b)+(a+b), где a+b=w- б.м.в.

x±y=(a±b)+w, то lim(x±y)=a±b=limx+limy.

2. Теорема о пределе производной: если сомножители имеют пределы, то и произведение имеет предел, равный произведению пределов сомножителей.

limx=a, limy=b, то на основании 5го св-ва

x=a+a

y=b+b, где a и b - б.м.в.

x*y=(a+a)*(b+b)=a*b+(ab+ab+ab), то

­сумма б.м.в. = d(дельта)

xy=ab+d

xy®ab,

limxy=ab=limx*limy

3. Следствие: постоянная величина выноситься за знак предела.

limCx=limC*limx=C*limx

4. Предел от частного = частному пределов (кроме limx/limy=0

limx/y=limx/limy, т.к. limx=a, limy=b

x=a+a, y=b+b

x/y=(a+a)/(b+b)

1й: limsinx/x=1, limx/sinx=1. x®0

j

lim((Sina)/a)=1

x®0

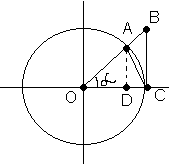
S_DOAC<S_{сектораOAC}<S_DOCB

S_DOAC=1/2*OC*AD, OA=OC=1, то

S_DOAC=1/2*OC*OA*Sina=1/2*Sina

S_{сектораOAC}=1/2*OA*OC*a=1/2*a(т.к. OA=OC)

S_DOCB=1/2*OC*BC=1/2*OC*OC*tga=1/2*tga

1/2*Sina<1/2*a<1/2tga //*2

sina<a<tga//:sin

1<a/sina<1/cosa, =>cosa<sina/a<1,

limCosa<lim((Sina)/a)<lim1, по признаку существования

a®0 a®0 предела ф-ции

lim((Sina)/a)=1

a®0

2ой: lim(1+1/n)ⁿ=e»2.7183

n®¥

Зная, что 1/n=a - б.м.в., то n=1/a и

x®¥ a®0

lim(1+1/n)^1/a=e

a®0

1. Подстановка: при х®х₀ и х₀Îобласти определения ф-ции f(x), предел ф-ции f(x)= его частному значению при х=х₀

limf(x)=f(x₀)

x®x₀

2. Сокращение: при х®¥ и х®х₀ f(x)/g(x)=0/0, то сокращают числитель и знаменатель на множитель, стремящийся к 0.

3. уничтожение иррациональности (* числитель и знаменатель на 1 число).

4.деление на наивысшую степень х: при х®¥ и х®х₀ f(x)/g(x)=0/0, то делим числитель и знаменатель на наивысшую степень.

5. сведение к известным пределам: lim((Sinx)/x)=1

x®¥

lim(1+1/n)^x=e

x®¥

Дата добавления: 2014-11-16