
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Производная 2го порядка ф-ции нескольких переменных. Дифференцирование сложной ф-ции 2х переменных
|
|
|
|
А) Частная производная ф-ции нескольких переменных. б) Частный и полный дифференциалы.
Предел и непрерывность ф-ции нескольких переменных.
Асимптота графика ф-ции.
Асимптота - прямая, к которой график ф-ции стремится, но никогда ее не пересекает.
1) прямая х=х0 назыв-ся вертикальной асимптотой графика ф-ции f(x)=y, если при х®х0 |f(x)|®+¥ (вида x=b)
2) y=kx+b,,y=f(x) - общее ур-е наклонной асимптоты
lim[f(x)-(kx+b)]=0, f(x)=kx+b+a(б.м.в.) по св-ву x®¥ пределов.
разделим левую и правую части на х. Возьмем предел при х®¥
f(x)/x=k+b/x+a/x, lim(f(x)/x)=limk+lim(b/x)+lim(a/x)
x®¥
, то
k=lim(f(x)/x)
b=lim[f(x)-kx]
Если эти пределы существуют, то существует и наклонная ассимптота вида kx+b=y
3)k=lim(f(x)/x)=0, y=b - горизонтальная асимптота.
Величина U наз-ся ф-цией переменных (x1,x2...xn), если каждой, рассматриваемой в совокупности этих величин соотв-ет 1 определенное значение величины U.
Пусть f(M)=M0(x10, x20,... xn0), M(x1, x2,... xn)
Ф-ция f(M)=f(x1, x2,... xn) имеет предел А при М0®М, если каждому значению как угодно малого числа d(дельта) соотв-ет, как угодно малое заданное число e>0, если | M0M |=d, то |f(M)-A|<e
Ф-ция f(M) наз-ся непрерывной в точке М0, если б.м. приращению любого аргумента соответствует б.м. приращение ф-ции.
limf(x10, x20,... xn0)=limf(x1, x2,... xn)
x10 ® x1
x20 ® x2
xn0 ® xn
а) рассмотрим на примере ф-ции 2х переменных
x=f(x,y), точка A(x0,y0)
Dz=f(x0+Dx, y0+Dy)-f(x0,y0) - полное приращение.
Частное приращение по х (по у):
DxZ=f(x0+Dx, y)-f(x0, y0)
DyZ=f(y0+Dy, x)-f(x0, y0)
Частная производная ф-ция:
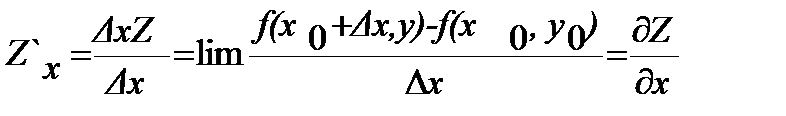
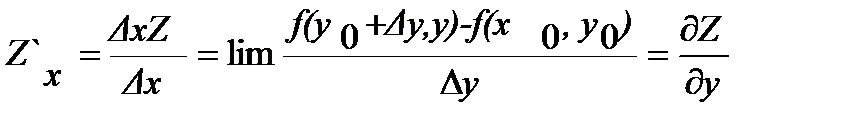 б) dxZ=Zx`*Dx=¶Z/¶x*dx; dxZ=Zy`*Dy=¶Z/¶y*dy
б) dxZ=Zx`*Dx=¶Z/¶x*dx; dxZ=Zy`*Dy=¶Z/¶y*dy
Полный дифференциал dZ=dxZ+dyZ=Z`xdx +Z`ydy
dZ=¶Z/¶x*dx+=¶Z/¶y*dy
Чтобы найти полный дифференциал ф-ции надо найти частные производные от этой ф-ции по всем независимым переменным, умножить их на дифференциал этих переменных, рез-ты сложить.
Частное производной 2го порядка от ф-ции Z явл. частная производная от 1й производной:
Z``XX=(Z`x)`x; Z``yy=(Z`y)`y
Z``Xy=(Z`x)`y=(Z`y)`x
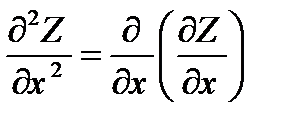
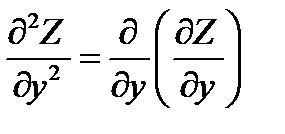
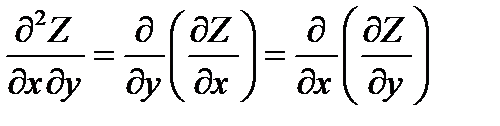
|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 564; Нарушение авторских прав?; Мы поможем в написании вашей работы!