Пример № 2

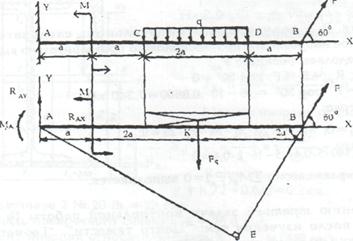
Задание

Для консольной балки, нагруженной равномерно распределенной нагрузкой интенсивностью q, силой F и парой сил с моментом М, определить опорные реакции заделки, если q = 20 кН/м, F= 10 кН, М =5 кН м, а = 0,4 м.

Решение

1.Выбираем систему координат хАу, совмещая ось х с балкой, а ось у, направляя перпендикулярно оси х. Освобождаем балку от связей и прикладываем реакции связей: реактивный момент М_А и составляющие реакции R_A по осям координат R_AX и R_AY. Равнодействующую равномерно распределенной нагрузки Fq = q · 2а = 20 · 2 ·0,4 = 16 кН, приложенную в точке пересечения диагоналей прямоугольника, переносим по линии ее действия в середину участка CD — в точку К.

2. Для полученной плоской системы сил составляем 3 уравнения
равновесия и определяем опорные реакции.

2.1 Определяем реактивный момент М_A

∑М_A(F_K)=0: M_A-M + F_q 3a-F · AE=0.

Определяем плечо силы F относительно точки А. Для того из точки А опускаем перпендикуляр АЕ на линию действия силы F. Из ∆ ABE определяем плечо силы F: АЕ=АВ · sin60°=5а sin60°=5 · 4 · 0.8560=1.732 м

2.2 Определяем реакцию r_ax

ΣF_AX=0; r_AX +F ·cos60° =0;

R_AX=-F · cos60° = -10 ·0.5 кН.

Реакция R_AX получилась отрицательной, следовательно, ее действительное направление противоположно предварительно выбранному.

2.3 Определяем реакцию R_AY:

ΣF_XY =0; R_AY –F + F · cos30° =0

R_AY=F_q-F · cos30° =16-10 · 0,8660 = 7,340 кН.

3. Проверка:

ΣM_B (F_K) = 0; M_A+R_AY · 5a - M-F_q · 2a = 0;

3,120 + 7,340 · 5 ·0,4 -5-16 ·2 ·0,4=0

Условие равновесия ΣM_B (F_K)= 0 выполняется.

К решению третьей задачи контрольной работы № 1 нужно приступить после изучения тем: "Центр тяжести", "Геометрические характеристики плоских сечений". При определении координат центра тяжести площади сложного сечения следует помнить, что центр тяжести прямоугольника располагается в точке пересечения его диагоналей, а координаты центра тяжести прокатных профилей необходимо определять с помощью таблиц сортаментов, в которых указаны размеры и координаты центра тяжести двутавров, швеллеров и уголков. При расчете на прочность и жесткость деталей, испытывающих кручение и изгиб, а также в расчетах на устойчивость сжатых стержней фигурируют некоторые характеристики, определяющие способность тела сопротивляться деформированию. Такими характеристиками, значения которых зависят от размеров и формы тела, являются моменты инерции сечений. В предлагаемых задачах также требуется определить главные центральные моменты инерции, то есть осевые моменты инерции сечения относительно его главных центральных осей. Напоминаем, что в сечении с двумя осями симметрии эти оси и являются главными центральными; в сечении с одной осью симметрии вторая главная центральная ось проходит через центр тяжести сечения перпендикулярно первой.

Дата добавления: 2014-11-18