Пример № 3

Задание

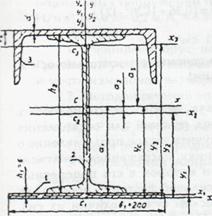
Определить главные центральные моменты инерции для поперечного сечения, составленного из листа 1 сечением 6 х 200 мм, двутавра 2 № 20 и швеллера 3 № 18.

Решение

1. Выбираем оси координат X₀ и У₀, как показано на рисунке. Для листа вычисляем, а для двутавра и швеллера выбираем из таблиц прокатной стали геометрический характеристики и

необходимые размеры.

Для листа 1.

Площадь поперечного сечения:

А₁ = h₁b₁ =0,6 · 20 = 12 см²:

Момент инерции относительно оси X₁;

J_х1= см⁴

Момент инерции относительно оси У_1;

J_Y1=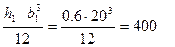

Координаты центра тяжести х₁=0. y₁ = h₁ /2 = 0,6/2=0,3 см.

Для двутавра 2 № 20 (h₂ =20 см)

Площадь поперечного сечения А₂ = 26,8 см²;

Момент инерции относительно оси Х₂ J_k2=1840 см⁴;

Момент инерции относительно оси У₂ J_v2=115 см⁴;

Координаты центра тяжести: X₂=0, Y₂=h₁+ 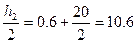см

Для швеллера 3 № 18 (Z₀= 1,94 см, d=0,51 см) Площадь поперечного сечении A₃ =20.7 см² ; Момент инерции относительно оси X₃ JX3=86см^4; Момент инерции относительно оси У₃ JY3=1090 см⁴; Координаты центра тяжести: Х₃ = 0. У₃ = h₁ +h₂+d -Z =0.6+20 +0,51-1,94=19,17 см.

2. Определяем координаты центра тяжести сечения:

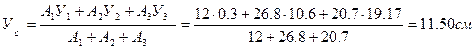
3. Определяем главные центральные моменты инерции сечения. Одной из главных центральных осей является ось симметрии У другая главная центральная ось X проходит через центр тяжести С сечения перпендикулярно оси У. Определяем расстояния между центральными осями X₁, Х₂ и Х₃ и главной центральной осью X:

a₁ =У_c-У₁=11.50-0.30=11.20см;

а₂ = У_с -У₂= 11,50 - 10.60 = 0.90 см;

3₃ = У_с-У₃= 19.17-11,50 = 7.67 см.

Главные центральные моменты инерции сечения определяем как алгебраическую сумму моментов инерции его частей.

Главный центральный момент инерции сечения относительно оси X:

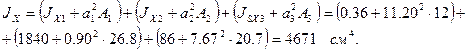
Главный центральный момент инерции сечения относительно оси У: J_У=Jу₁+ Jу₂ + Jу₃ = 400+115+1090=1605 cm⁴.

Приступая к решению четвертой задачи, необходимо проработать тему "Растяжение и сжатие", изучить метод сечений для определения внутренних силовых факторов и следует получить четкое представление о видах нагружения, напряжениях, перемещениях. Растяжением (сжатием) называют такой вид деформации бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор- продольная сила N. которая численно равна алгебраической сумме величин их сил, действующих на оставленную часть: N=ΣF. При растяжении продольная сила положительна, а при сжатии — отрицательна. При растяжении и сжатии в поперечном сечении бруса возникают нормальные напряжения

,

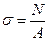где А — площадь поперечного сечения бруса. Удлинения (укорочения) отдельных участков бруса определяются по формуле:

,

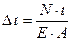где 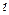— длина соответствующего участка, Е — модуль упругости 1 рода.

Дата добавления: 2014-11-18