Пример № 6

1.Определяем реакции опор:

Задание

Для двухопорной балки
определить реакции опор,
построить эпюры поперечных сил
и изгибающих моментов. Найти
максимальный изгибающий
момент и подобрать необходимые
размеры "b" и "h" деревянной
балки прямоугольного поперечного сечения, приняв h=2b и [σ]=10Н/мм², если q=20 кН/м, F= 10 кН, М = 5 кН м, а=0.4 м.

Решение

ΣМ_А (F_K) =0; q·2a·2a-F4·a-M-R_b·6a=0;

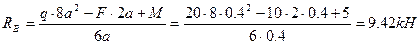
Проверка: ΣF_KУ=0; R_A-q·2a+F-R_B=0; 9,42-20·2·0,4+10-3,42=0; 0=0

2. Разбиваем балку на 5 участков и определяем поперечную силу Q_У для каждого участка:

Q_У1= R_A = 9.42KH; Q_У2=R_A-q(х-а), _;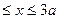

при х = a Q_У2= r_A = 9,42 кН; при х = За Q_У2= R_А –q·2a= 9,42 - 20·2· 0,4=6.54кН

Q_У3 = R_B-F = 3,42-10=-6,58 кН;

Q_У4= R_В = 3.42 кН; Q_У3= Q_У4 = 3.42 кН.

Эпюру поперечных сил Q_У строим в масштабе μ_Q=1кН/мм

3. Определяем положение сечения С, в котором Q_У=0:

Q_УC =R_A-q(x-a)=0, откуда x_C = R_A/q + a= 9,42/20+ 0,4 = 0,871 м.

4. Определяем изгибающий момент M_Z для каждого участка:

m_Z1 = R_A·x,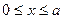

при х=0 M_Z1=0;

при х=а M_Z1 = R_A·а=9,42·0,4 = 3,768 кН м.

M_Z2 ⁼ R_A· x-q(x-a)²/2, a<x<3a;

при х=а M_Z2=R_A·a= 9,42·0,4=3,768кНм;

при x=3a M_Z2=R_A·3a-q·2a²=9,42·3·0,4-20·2·0.42=4.900 кН·м;

при х=х_C

М_Z3 = -R_Bx + М + F(x - 2а), 2а х За

при х=3а М_Z3=-R_B·3a+М + F·а=-3,42·3·0.4+5+10·0.4=4.900 кН·м; при х=2а М_Z3=-R_B·2a+M=-3,42·2·0,4+5 = 2.2 кН·м.

M_Z4=-R_Bx+ M, а х 20;

при х = 2а M_Z4 =-R_B·2a + M =-3,42 ·2·0,4+5 = 2,264 кН·м; при х = а M_Z4 =-R_Ba + M= -3.42·0.4 +5 = 3.632 кН·м. M_Z5=-R_Bx, 0 х a;

при х = а M_Z5 =-R_Ba =-3,420·,4 = -1,368 кН·м;

при х=0 M_Z5=0.

Эпюру изгибающих моментов M_Z строим в масштаб μ_M=0,5 кН·м/мм

5.Исходя из эпюры изгибающих моментов, М_Zmax=5.987 кН·м. Требуемый осевой момент сопротивления при изгибе:

Для прямоугольника момент сопротивления

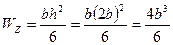, откуда: ширина сечения 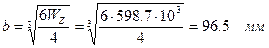; высота сечения h=2b=2·96.5=193 мм.

Дата добавления: 2014-11-18