Пересчёт тензора инерции

Пример

Момент инерции стержня относительно оси, проходящей через его центр и перпендикулярной стержню, (назовём её осью ) равен

Тогда согласно теореме Штейнера его момент относительно произвольной параллельной оси будет равен

где 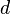— расстояние между искомой осью и осью . В частности, момент инерции стержня относительно оси, проходящей через его конец и перпендикулярной стержню, можно найти положив в последней формуле :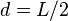

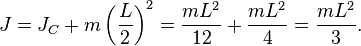
Теорема Гюйгенса — Штейнера допускает обобщение на тензор момента инерции, что позволяет получать тензор 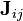относительно произвольной точки из тензора 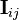относительно центра масс. Пусть — смещение от центра масс, тогда

где

— вектор смещения от центра масс, а — символ Кронекера.

Как видно, для диагональных элементов тензора (при 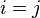) формула имеет вид теоремы Гюйгенса — Штейнера для момента относительно новой оси.

6 вопрос: идеальная жидкость. Ламинарное и турбулентное течение идеальной жидкости. Уравнение Бернулли.

Идеа́льная жи́дкость — в гидродинамике — воображаемая жидкость (сжимаемая или несжимаемая), в которой отсутствуют вязкость и теплопроводность. Так как в ней отсутствует внутреннее трение, то нет касательных напряжений между двумя соседними слоями жидкости.

Моделью идеальной жидкости пользуются при теоретическом рассмотрении задач, в которых вязкость не является определяющим фактором и ею можно пренебречь. В частности, такая идеализация допустима во многих случаях течения, рассматриваемых гидроаэромеханикой, и даёт хорошее описание реальных течений жидкостей и газов на достаточном удалении от омываемых твёрдых поверхностей и поверхностей раздела с неподвижной средой. Математическое описание течений идеальных жидкостей позволяет найти теоретическое решение ряда задач о движении жидкостей и газов в каналах различной формы, при истечении струй и при обтекании тел.

Существует два режима течения жидкостей. Течение называется ламинарным (слоистым), если вдоль потока каждый выделенный тонкий слой скользит относительно соседних, не перемешиваясь с ними, и турбулентным (вихревым), если вдоль потока происходит интенсивное вихреобразование и перемешивание жидкости (газа).

Ламинарное течение жидкости как правило наблюдается при небольших скоростях ее движения. Внешний слой жидкости, примыкающий к поверхности трубы, в которой она течет, из-за сил молекулярного сцепления прилипает к ней и остается неподвижным. Скорости последующих слоев тем больше, чем больше их расстояние до поверхности трубы, при этом наибольшей скоростью обладает слой, который движется вдоль оси трубы.

При турбулентном течении частицы жидкости приобретают составляющие скоростей, которые перпендикулярны течению, и они могут двигаться из одного слоя в другой. Скорость частиц жидкости быстро возрастает по мере удаления от поверхности трубы, затем изменяется незначительно. Так как частицы жидкости могут перейти из одного слоя в другой, то их скорости в различных слоях мало отличаются. Из-за большого градиента скоростей у поверхности трубы обычно происходит образование вихрей.

Профиль усредненной скорости при турбулентном течении в трубах (рис. 2) отличается от параболического профиля при ламинарном течении в трубах более быстрым возрастанием скорости у стенок трубы и меньшей кривизной в центральной части течения.

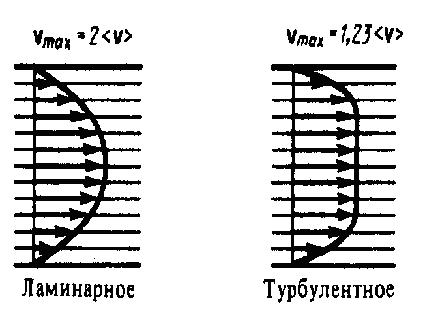
Рис.2

Характер течения зависит от безразмерной величины, называемой числом Рейнольдса (О. Рейнольдс (1842-1912) - английский ученый):

где ν = η/ρ - кинематическая вязкость; ρ-плотность жидкости; <v>-средняя по сечению трубы скорость жидкости; d - характерный линейный размер, например диаметр трубы.

При малых значениях числа Рейнольдса (Re≤1000) наблюдается ламинарное течение, область перехода от ламинарного течения к турбулентному происходит при 1000≤Re≤2000, а при Re=2300 (для гладких труб) течение - турбулентное. Если число Рейнольдса одинаково, то режим течения различных рассматриваемых жидкостей (газов) в трубах разных сечений одинаков.

Закон (уравнение) Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:

Здесь

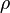— плотность жидкости,

— скорость потока,

— высота, на которой находится рассматриваемый элемент жидкости,

— давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,

— ускорение свободного падения.

В научной литературе закон Бернулли, как правило, называется уравнением Бернулли ^[1](не следует путать с дифференциальным уравнением Бернулли), теоремой Бернулли ^[2][3] или интегралом Бернулли ^[4][5].

Константа в правой части часто называется полным давлением и зависит, в общем случае, от линии тока.

Размерность всех слагаемых — единица энергии, приходящаяся на единицу объёма жидкости. Первое и второе слагаемое в интеграле Бернулли имеют смысл кинетической ипотенциальной энергии, приходящейся на единицу объёма жидкости. Следует обратить внимание на то, что третье слагаемое по своему происхождению является работой сил давления (см. приводимый в приложении вывод уравнения Бернулли) и не представляет собой запаса какого-либо специального вида энергии («энергии давления»^[6]).

Соотношение, близкое^[7] к приведенному выше, было получено в 1738 г. Даниилом Бернулли, с именем которого обычно связывают интеграл Бернулли. В современном виде интеграл был получен Иоганном Бернулли около 1740 года.

Для горизонтальной трубы высота постоянна и уравнение Бернулли принимает вид: .

Эта форма уравнения Бернулли может быть получена путём интегрирования уравнения Эйлера для стационарного одномерного потока жидкости, при постоянной плотности : .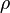

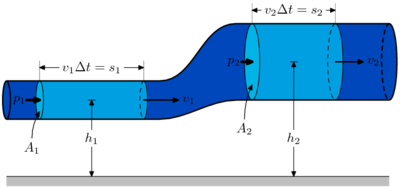
Согласно закону Бернулли, полное давление в установившемся потоке жидкости остается постоянным вдоль этого потока.

Полное давление состоит из весового , статического 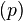и динамического 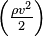давлений.

Из закона Бернулли следует, что при уменьшении сечения потока, из-за возрастания скорости, то есть динамического давления, статическое давление падает. Это является основной причиной эффекта Магнуса. Закон Бернулли справедлив и для ламинарных потоков газа. Явление понижения давления при увеличении скорости потока лежит в основе работы различного рода расходомеров (например труба Вентури), водо- и пароструйных насосов. А последовательное применение закона Бернулли привело к появлению технической гидромеханической дисциплины — гидравлики.

Закон Бернулли справедлив в чистом виде только для жидкостей, вязкость которых равна нулю. Для приближённого описания течений реальных жидкостей в технической гидромеханике (гидравлике) используют интеграл Бернулли с добавлением слагаемых, учитывающих потери на местных и распределенных сопротивлениях.

Известны обобщения интеграла Бернулли для некоторых классов течений вязкой жидкости (например, для плоскопараллельных течений^[8]), в магнитной гидродинамике^[9],феррогидродинамике^[10].

· закон Бернулли объясняет эффект притяжения между телами, находящимися вблизи границ потоков движущихся жидкостей (газов). Иногда это притяжение может создавать угрозу безопасности. Например, при движении скоростного поезда «Сапсан» (скорость движения более 200 км/час) для людей на платформах возникает опасность сброса под поезд.^[12] Аналогично «затягивающая сила» возникает при движении судов параллельным курсом^[13]: например, подобные инциденты происходили с лайнером «Олимпик».

· Автоаварии: проносящиеся мимо многотонные грузовики с прицепами притягиваются к стоящему на обочине автострады автомобилю. Это одна из опасностей, которыми объясняют запрет на остановку автомобилей на обочинах автострад.

7 вопрос: термодинамическое равновесие и температура. Уравнение состояния в термодинамике.

Дата добавления: 2014-11-08