
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Апроксимація табличних функцій степеневими поліномами
|
|
|
|
Розглянемо загальні математичні моделі, які можна отримати при апроксимації табличних функцій степеневим поліномом.
Постановка задачі
В результаті інженерного або наукового експерименту отримана система точок  . Необхідно знайти степеневий поліном виду:
. Необхідно знайти степеневий поліном виду:
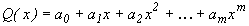 , (6.4)
, (6.4)
такий, щоб сума квадратів відхилень полінома 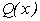 від заданої системи експериментальних точок була би мінімальною. Така задача зводиться до визначення коефіцієнтів поліному
від заданої системи експериментальних точок була би мінімальною. Така задача зводиться до визначення коефіцієнтів поліному  . Метод, що дозволяє розв’язати її називається методом найменших квадратів (МНК). Критерій середньо квадратичного відхилення (СКО) в даному випадку має вигляд:
. Метод, що дозволяє розв’язати її називається методом найменших квадратів (МНК). Критерій середньо квадратичного відхилення (СКО) в даному випадку має вигляд:
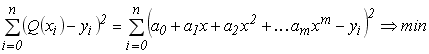 (6.5)
(6.5)
Розглянемо рисунок 6.1.
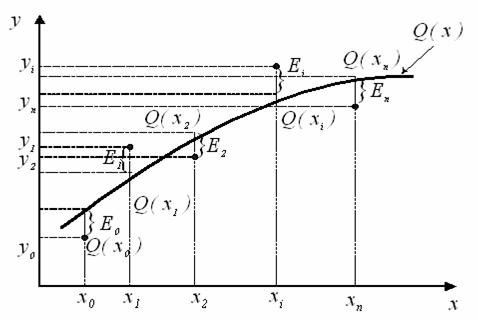
Рисунок 6.1 - Геометрична інтерпретація апроксимації табличної функції
З нього видно, що
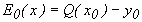 ,
, 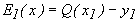 ,...,
,..., 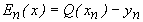 ,
,
тому вираз (6.5) можна представити в вигляді:
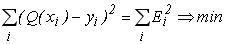
Очевидно, що функція E - це багато параметрична функція на множині 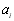 ,
, 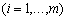 . Мінімуму такої функції знаходиться при виконанні умови виду:
. Мінімуму такої функції знаходиться при виконанні умови виду:
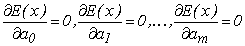 (6.6)
(6.6)
Підставимо в (6.6) заміст функції 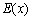 - вираз
- вираз 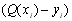 , та заміст
, та заміст 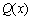 з (6.4) підставимо поліном і визначимо частинні похідні в виразу (6.6) по кожному коефіцієнту
з (6.4) підставимо поліном і визначимо частинні похідні в виразу (6.6) по кожному коефіцієнту 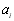 . В результаті отримуємо систему рівнянь виду:
. В результаті отримуємо систему рівнянь виду:

В даної системі розкриємо дужки та спростимо кожне рівняння системи окремо. В результаті отримаємо систему виду:
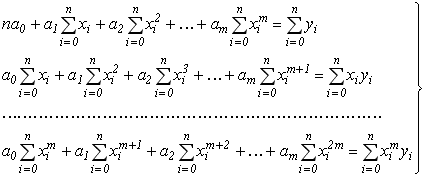 (6.7)
(6.7)
Система рівнянь (6.7) представляє собою систему лінійних алгебраїчних рівнянь відносно коефіцієнтів поліному 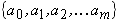 , які необхідно знайти, щоб визначити аналітичну залежність, яка описує експериментальний масив даних. Дану систему можна записати у матричному вигляді:
, які необхідно знайти, щоб визначити аналітичну залежність, яка описує експериментальний масив даних. Дану систему можна записати у матричному вигляді:
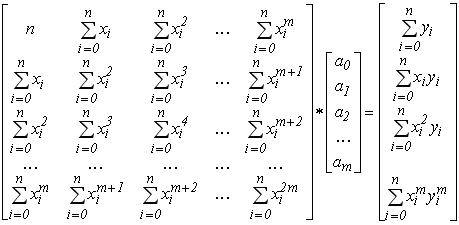
Для розв’язання такої системи на ЕОМ необхідно розробити спеціальний алгоритм та підпрограму для формування її матриці коефіцієнтів та вектора вільних членів з використанням експериментальних даних, які задані таблицею. На рисунку 6.2 представлений алгоритм формування системи лінійних алгебраїчних рівнянь (6.7) запропонований Делем В.Д. В ньому система (6.7) формується з метою зменшення кількості обчислювальних операцій (наприклад операції обчислення степеня), для цього введені допоміжні змінні та масиви 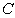 і D. Зміна
і D. Зміна 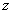 - містить поточне значення
- містить поточне значення 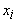 ;
; 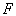 - поточне значення
- поточне значення 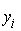 ;
;  - множник, який багаторазово змінюється в процесі обчислення;
- множник, який багаторазово змінюється в процесі обчислення; 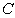 - допоміжний масив із
- допоміжний масив із 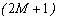 дійсних чисел, який являє собою суми
дійсних чисел, який являє собою суми 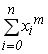 (
(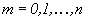 ), що входять в кожне рівняння системи:
), що входять в кожне рівняння системи:
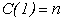 ,
, 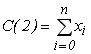 ,...,
,..., 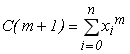 ,...,
,..., 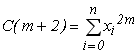
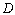 - масив із
- масив із 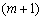 дійсних чисел, які являють собою суми вектора-стовпця вільних членів системи рівнянь (6.7) і визначають за допомогою допоміжних змінних
дійсних чисел, які являють собою суми вектора-стовпця вільних членів системи рівнянь (6.7) і визначають за допомогою допоміжних змінних 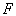 та
та  :
:
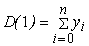 ,
, 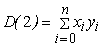 ,
, 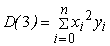 ,
, 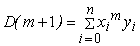
Розв‘язувати таку систему можна будь-яким з відомих методів розв‘язання системи лінійних алгебраїчних рівнянь, наприклад методом Гауса. Однак задача апроксимації на цьому етапі не завершується. Схема алгоритму побудови СЛАР методом Деля В.Д (6.7). представлена на рисунку 6.2.

Рисунок 6.2– Схема алгоритму побудови СЛАР методом В.Д. Деля
Якщо для заданого степеня  поліному
поліному 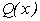 в результаті розрахунків на ЕОМ отриманий поліном не відповідає заданої похибки обчислень
в результаті розрахунків на ЕОМ отриманий поліном не відповідає заданої похибки обчислень 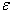 , то необхідно збільшити ступень поліному на 1 (тобто степінь полінома буде
, то необхідно збільшити ступень поліному на 1 (тобто степінь полінома буде 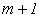 ), при цьому на одиницю збільшується кількість коефіцієнтів поліному (додається новий член степеневого поліному), які необхідно знову розраховувати. При цьому розмір системи (6.7) збільшується на 1, і для визначення нових коефіцієнтів
), при цьому на одиницю збільшується кількість коефіцієнтів поліному (додається новий член степеневого поліному), які необхідно знову розраховувати. При цьому розмір системи (6.7) збільшується на 1, і для визначення нових коефіцієнтів 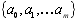 необхідно знову розв’язувати систему (6.7) методом Гауса. Цей процес повторюється до тих пір, поки не виконається умова
необхідно знову розв’язувати систему (6.7) методом Гауса. Цей процес повторюється до тих пір, поки не виконається умова
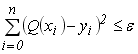 , (6.8)
, (6.8)
де 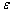 - задана похибка отриманих результатів.
- задана похибка отриманих результатів.
Схема алгоритму апроксимації функцій, заданих таблицею, методом найменших квадратів представлена на рисунку 6.3.
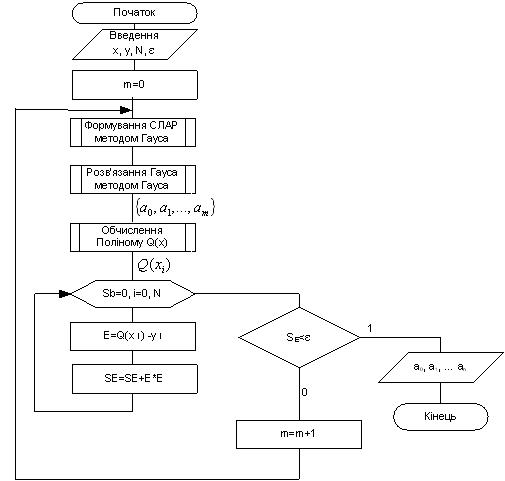
Рисунок 6.3 – Схема алгоритму апроксимації функцій, заданих таблицею, методом найменших квадратів
|
|
|
|
|
Дата добавления: 2014-11-08; Просмотров: 1247; Нарушение авторских прав?; Мы поможем в написании вашей работы!