Основні поняття та визначення. Інженеру часто приходиться обчислювати визначений інтеграл чисельними методами

ЧИСЕЛЬНІ МЕТОДИ ЗНАХОДЖЕННЯ ІНТЕГРАЛУ ЗА ДОПОМОГОЮ КВАДРАТУРНИХ МЕТОДІВ ОБЧИСЛЕННЯ

Лекція № 7

Інженеру часто приходиться обчислювати визначений інтеграл чисельними методами. Це буває у тих випадках, коли або не вдається виразити інтеграл у замкненій формі, або вона настільки складна, що простіше скористатися чисельним інтегруванням. Чисельне інтегрування являє собою стійкий процес і в протиставлення чисельному розв’язанню диференційних рівнянь зменшує дію похибок у початкових даних на кінцевий результат.

Розглянемо функцію f(x), що визначена на відрізку [a,b]. Функція, що диференціюється на відрізку [a,b] функцією F(x), похідна якої в кожній точці [a,b] дорівнює f(x), називається первісною функції f(x) та записується як:

F’(x)= f(x).

Так як (F(x)+С)’=F’(x)=f(x) для будь-якої сталої С, то можна говорити про множину первісних – множину функцій виду F(x)+С. Множина первісних F(x)+С функції f(x) називається невизначеним інтегралом функції f(x) і позначається :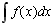

,

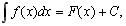
де F(x)+С – значення невизначеного інтегралу, тобто множини первісних функції f(x):

()’=(F (x)+ С)’= f (x).

Розглянемо функцію f (x), що визначена на відрізку [a,b]. Розіб’ємо відрізок [a,b] на n довільних частин точками a=x₀< x₁< x₂<…< x_n-1< x_n=b

і позначимо 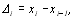i=1,...,n, .

На кожному відрізку[ x_i-1, x_i ] візьмемо довільну точку 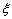_i і обчислимо в неї значенняфункції f (x). Вираз

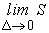називається інтегральною сумою функції f (x).Якщо при існує границя , не залежна ні від способу розбиття відрізку [a,b] точками x_i, i=1,2,…,n-1, ні від вибору точок 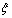_i (x_i1, x_i), то ця границя називається визначеним інтегралом від функції f (x) на відрізку [a,b], а саму функцію – інтегрованою на [a,b], та позначають як

Розглянемо геометричний зміст визначеного інтегралу: якщо f(x)>0, то 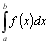дорівнює площі фігури, обмеженої графіком функції, віссю абсцис і прямими і 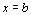(рис.7.1).

Рисунок 7.1 – Геометричний зміст інтегралу.

В основу чисельного інтегрування покладене наближене обчислення площини під кривою, яка описується підінтегральною функцією інтеграла виду

.

Розглянемо загальний підхід до розв'язування цієї задачі на ЕОМ.

Визначений інтеграл І являє собою площину, обмежену кривою f(x), віссю х та прямими х = a; х = b (рис.7.1).

Чисельне інтегрування основане на тому, що відрізок інтегрування [a,b] розбивають на n менших відрізків [ x_i-1, x_i ], кожен з яких є основою геометричної фігури, площу якої знаходять наближено як S_i, а значення інтегралу І визначають як суму таких площин S_i, тобто

.

При цьому використовують два способи розбиття відрізка інтегрування на менші:

1. Розбиття відрізка інтегрування проводиться раніше аналізу результатів інтегрування, до того ж завжди відрізки вибирають рівними (метод прямокутників, трапецій, Сімпсона);

2. Місцезнаходження та довжина відрізків визначаються з умови досягти найбільшої точності чисельного інтегрування з заданим числом відрізків, а потім відповідно з цим визначають їхні межі (метод Гаусса, Ньютона-Котеса, Чебишева).

Дата добавления: 2014-11-08