Метод Чебишева

Метод Ньютона-Котеса

ЧИСЕЛЬНІ МЕТОДИ ЗНАХОДЖЕННЯ ІНТЕГРАЛУ ЗА ДОПОМОГОЮ АЛГЕБРАЇЧНИХ ФУНКЦІЙ

Лекція № 8

Метод Ньютона-Котеса засновано на інтерполяції однієї із сторін криволінійних трапецій, що отримані поділом відрізку інтегрування [а,b] на N рівних частин, багаточленами більш високих порядків ніж в методі трапецій (де використовується лінійна інтерполяція) і в методі Сімпсона (де використовується квадратична інтерполяція).

Основна формула методу Ньютона-Котеса має вигляд:

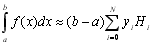, (8.1)

де 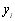- значенняпідінтегральної функції f(x) в вузлах інтерполяції, Hi – коефіцієнти Ньютона-Котеса, які не залежать від вигляду підінтегральної функції f(x), а залежать тільки від N (кількості вузлів інтерполяції), тому значення їх для різної кількості вузлів відомі та представлені в таблиці 8.1. Можна показати, що методи трапецій та Сімпсона є частинними випадками методу Ньютона-Котеса.

Таблиця 8.1 - Коефіцієнти Ньютона-Котеса

n=1	ho=h1=1/2
n=2	ho=h2=1/6, h1=2/3
n=3	ho=h3=1/8, h1=h2=3/8
n=4	ho=h4=7/90, h1=h3=16/45, h2=2/15
n=5	ho=h5=19/288, h1=h4=25/96, h2=h3=25/144
n=6	ho=h6=41/840, h1=h5=9/35, h2=h4=9/280, h3=34/105
n=7	ho=h7=751/17280, h1=h6=3577/17280, h2=h5=1323/17280, h3=h4=2989 /17280

На відміну від методу Ньютона-Котеса, в якому коефіцієнти H_i (i=1,N) знаходять у фіксованих вузлах інтерполяції, П.Л. Чебишев запропонував для обчислення визначених інтегралів використати формулу

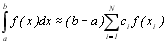, (8.2)

в якій квадратурні коефіцієнти С_i (і=1,2,…,N) зафіксовані, а абсциси x_i (і=1,2,…,N) підлягають визначенню. Для простоти обчислень необхідно вибрати С₁=С₂=…=С_n. Розглянемо спочатку частинний випадок, коли межі інтегрування дорівнюють –1 та 1. Тоді попередня формула набере вигляду

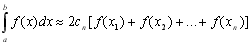, (8.3)

де квадратурні коефіцієнти С_n та абсциси x_i підлягають визначенню.

Коефіцієнти С_i та вузли інтерполяції x_i визначимо із умови, що ця рівність є точною для випадку, коли f(х) - багатогочлен вигляду

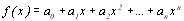(8.4)

Підставимо багаточлен (8.4) у ліву частину (8.3) та проінтегруємо:

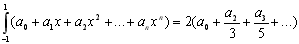(8.5)

У праву частину рівності (8.3) підставимо значення многочлена (8.4) у вузлах х₁, х₂, …,х_n:

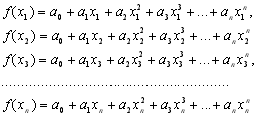(8.6)

Тоді формула (8.5) буде мати вигляд

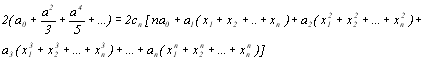(8.7)

Отримана рівність повинна виконуватися за будь-яких значень а_o,а₁,…,а_n і таким чином, порівнюючи коефіцієнти а_i в правій і лівій частинах (8.7) знаходимо, що nC_n=1, звідки

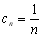(8.8)

i, крім цього,

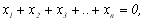
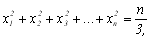
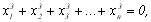(8.9)

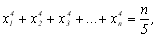
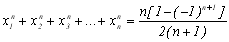
Підставляючи знайдене для С_n виразу в співвідношення (8.5) отримаємо формулу Чебишева:

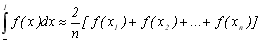(8.10)

де точки x₁,…,x_n визначаються із системи рівнянь (8.9).

Значення x₁,…,x_n для різних n відомі та представлені в таблиці 8.2.

Таблиця 8.2 - Значення абсцис для різної кількості точок

Число ординат	Значення абсцис
n=2	-x1=x2=0.577350
n=3	-x1=x3=0.707107; x2=0
n=4	-x1=x4=0.794654; -x2=x3=0.187592
n=5	-x1=x5=0.832498; -x2=x4=0.374541; x3=0
n=6	-x1=x6=0.866247; -x2=x5=0.422519; -x3=x4=0.266635
n=7	-x1=x7=0.883862; -x2=x6=0.529657; -x3=x5=0.323912; x4=0

Коли межі даного інтеграла відрізняються від –1 та 1, формула Чебишева матиме вигляд

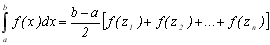, (8.11)

де

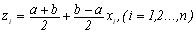. (8.12)

а x_i мають вказані в таблиці значення.

Дата добавления: 2014-11-08