Метод Гауса

Для отримання підвищеної точності для чисельного інтегрування користуються формулою Гауса

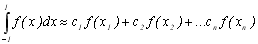, (8.13)

в якої не фіксуються не тільки вузли інтерполяції x₁, x₂,…,x_n, а й квадратурні коефіцієнти С₁,…,С_n. При цьому Z_n невідомих величин x₁,…,x_n; С₁,…,С_n визначається із умови, що формула є точною у випадку будь-якого багаточлена 2n-1.

Таким чином, для будь-якого багаточлена (2n-1)-й степеню

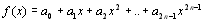(8.14)

повинна виконуватися рівність:

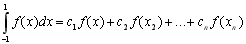. (8.15)

Багаточлен f(x) степеню 2n-1 можна показати у вигляді

f(x)=F(x)Q(x)+R(x), (8.16)

де F(x)- шуканий багаточлен n-ї степені, а Q(x) та R(X) - відповідно частинне ділення f(x) на F(x) та залишок від цього ділення, степінь багаточленів Q(x) та R(x) не перевищують (2n-1).

Вираз для F(x) можна записати так:

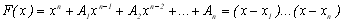(8.17)

тут величини x₁,…,x_n - шукані абсциси формули Гаусса, а А₁,А₂,…,А_n - постійні.

Оскільки шукана функція F(x) у вузлах x₁,…,x_n перетворюється на нуль, то

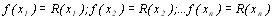(8.18)

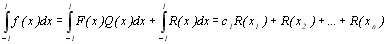(8.19)

Але для багаточлена R(x) степеню не вище n-1 також повинна виконуватися рівність:

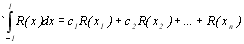(8.20)

Bіднімаючи (8.20) від (8.19),отримаємо

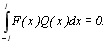
Із останнього відношення можна визначити шукану функцію F(x). Оскільки ця рівність справедлива для якого-небудь багаточлена Q(x) степеню n-1

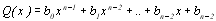, (8.21)

то при будь-яких коефіцієнтах 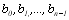маємо таку систему рівнянь:

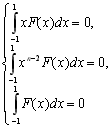(8.22)

Підставляючи в (8.22) вирази для F(x) із формули (7.2) та інтегруючи, отримаємо для визначення коефіцієнтів А₁, … А_n систему n рівнянь

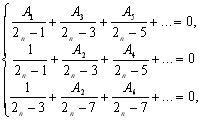(8.23)

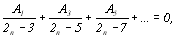
з яких видно, що А₁=А₃=А₅=А₇=…=0 та, отже, шуканий многочлен має вигляд:

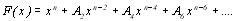(8.24)

Відмітимо, що при парному n корені рівняння F(x)=0 попарно рівні за абсолютним значенням, але протилежні за знаком, а при непарному n коренем є також і х=0.

Визначивши із системи (8.23) коефіцієнти А_і (і=1,2,…,n), складемо рівняння F(x)=0 та знайдемо його корені х₁,…,х_n, тобто шукані абсциси формули Гаусса, а потім обчислимо коефіцієнти С_i (і=1,2,…,n) за формулою

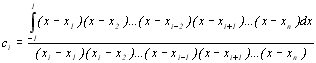(8.25)

Приклад 1. Побудувати квадратурну формулу Гаусса для випадку n=2 на відрізку інтегрування [-1, 1].

Розв‘язок. Загальний вигляд квадратурної формули Гаусса при n=2 та заданих межах інтегрування:

,

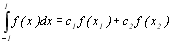де підлягають визначенню квадратурні коефіцієнти с₁ та с₂, а також абсцис х₁ та х₂.

Для визначення абсцис складемо многочлен 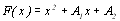, коефіцієнти А₁ та А₂ якого знайдемо із системи вигляду (8.22)

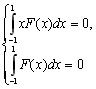
підстановкою багаточлена F(x) у систему. Маємо

; ,

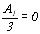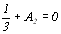тобто А₁=0, А₂ =-1/3. Тоді 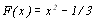, звідки

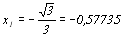та

Коефіцієнти с₁ та с₂ обчислимо за формулою (8.25)

;

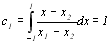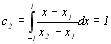
Отже,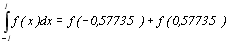

Для обчислення інтеграла загального вигляду 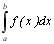слід замінити змінні

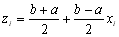, (i=1,2,….,n) (8.26)

Тоді формула Гаусса прийме вигляд

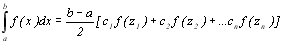
Значення квадратурних коефіцієнтів Гаусса с_і (і=1,2...n) та абсцис х_і (і=1,2...n) наведені в таблиці 8.3.

Таблиця 8.3 – Значення квадратурних коефіцієнтів Гаусса

n=1	x1=0,5	с1=2
n=2	-x1=x2=0,577350	с1=с2=1
n=3	-x1=x3=0,774597, x2=0	с1=с3=0,555555, с2=0,888889
n=4	-x1=x4=0,861136, -x2=x3=0,339981	с1=с4=0,347855, с2=с3=0,652145
n=5	-x1=x5=0,906180, -x2=x4=0,538470	с1=с5=0,236927, с2=с4=0,478629
n=6	-x1=x6=0,932470, -x2=x5=0,661210, -x3=x4=0,238620	с1=с6=0,171324, с2=с5=0,360761, с3=с4=0,467914
n=7	-x1=x7=0,949108, -x2=x6=0,741531, -x3=x5=0,405845, x4=0	с1=с7=0,129485, с2=с6=0,279705, с3=с5=0,381830, с4=0,417960
n=8	-x1=x8=0,960290, -x2=x7=0,796666, -x3=x6=0,525532, x4=0,183434	с1=с8=0,101228, с2=с7=0,222381, с3=с6=0,313707, с4=с5=0,362684,

Дата добавления: 2014-11-08