Количественные дуополии

Предположительные вариации

Рассмотрим олигополии, выпускающие однородную продукцию, а вход в отрасль считаем закрытым (т.е. число фирм в отрасли фиксировано, нет возможности другим фирмам войти в отрасль). Предположим также, что рассматриваемые в данном разделе модели являются моделями однократного взаимодействия.

Имея целью своей деятельности максимизацию прибыли и принимая решение об объеме производства, олигополист должен предвидеть реакцию конкурентов на изменение своего поведения.

П редположительная вариация - э то предположения олигополиста относительно реакции соперника в ответ на изменение своего собственного поведения.

Пусть в отрасли действуют n фирм, ориентированных на выпуск как стратегическую переменную и максимизирующих прибыль.

Фирмы имеют различные функции общих издержек ТС, и соответственно различные предельные издержки с_i.

Совокупный выпуск отрасли составляет Q = ∑q_i, (6.8)

где i = 1,2,...n.

Функция прибыли i-й фирмы отрасли:

П_i = P(Q)• q_i –ТС_i. (6.9)

Необходимое условие максимизации прибыли для i-и фирмы:

∂ П_i / ∂q_i = (∂(P(Q)• q_i) / ∂q_i) – c_i = ((∂P(Q) / ∂Q) • (∂Q / ∂q_i) q_i) + ((∂q_i / ∂q_i) P) - c_i

= P + ((∂P(Q) / ∂Q) • (∂Q / ∂q_i) q_i) - c_i = 0 (6.10)

Член ∂Q / ∂q_i показывает изменение совокупного выпуска отрасли в ответ на изменение выпуска i-и фирмы. Его можно представить как:

∂Q / ∂q_i = (∂q_i / ∂q_i) + (∂q_j / ∂q_i) = 1 + (∂q_j / ∂q_i) = 1 + λ_i (6.11)

λ_i в выражении (6.11) — предположительная вариация i-й фирмы. Она показывает предположения i-й фирмы в отношении того, как отреагирует выпуск остальных jфирм на изменение ее собственного выпуска. С учетом (6.11) необходимое условие максимизации прибыли для i-и фирмы (6.10) будет иметь следующий вид:

∂ П_i / ∂q_i = P + ((∂P(Q) / ∂Q) • (1 + λ_i) q_i) - c_i = 0 (6.12)

В модели олигополии Курно ключевой предпосылкой является равенство нулю предположительной вариации i-й фирмы в отношении того, как отреагирует выпуск остальных jфирм на изменение ее собственного выпуска., т.е.λ_i = 0.

Если в олигополии Курно участвует n фирм с одинаковыми предельными издержками с_i = с, то все фирмы будут иметь одинаковый выпуск, т.к. они будут иметь одинаковое уравнение, выражающее необходимое условие максимизации прибыли:

∂ П_i / ∂q_i = P + ((∂P(Q) / ∂Q) • q_i) – c = 0 (6.13)

Модель олигополии Курно

Модели олигополии Курно была разработана французским экономистом-математиком Огюстэном Курно еще в 1838 г и является одной из классических моделей количественной олигополии.

Дуополия Курно

Дуополия представляет собой олигополию, представленную всего двумя фирмами. Дуополия Курно представляет собой модель поведения олигополистов, в которой фирмы ориентированы на выпуск как стратегическую переменную, поэтому ее еще называют «количественной» олигополией. Дуополия Курнотакже является разновидностью моделей олигополии без сговора.

В этой модели фирмы выбирают объем выпуска, действуя одновременно и независимо друг от друга, что обусловлено предполагаемой однократностью взаимодействия. Согласно центральной предпосылке этой модели, каждая фирма-олигополист считает выпуск соперника постоянным, не реагирующим на изменения ее собственного выпуска. Иными словами, каждая фирма-олигополист стремится максимизировать свою прибыль, исходя их предпосылки о том, что ее соперники сохранят текущий уровень выпуска и при этой предпосылке принимают решения об уровне своего выпуска.

Рассмотрим вначале аналитическую версию модели, анализирующую стратегическое взаимодействие фирм при нулевых предполагаемых вариациях:

∂q₁ / ∂q₂=0, ∂ q₂ / ∂q₁=0.

Обе фирмы имеют одинаковые издержки, в т.ч. одинаковые и неизменные предельные издержки с на единицу выпуска:

TC(q₁)=, TC(q₂) =сq, (6.14)

МС=АС=с. (6.15)

Функция прибыли для фирмы 1 и 2:

П₁ = ТR ₁- ТС₁ =P(q₁ + q₂)q₁ – ТС(q₁) (6.16)

П₂ = ТR ₂- ТС₂ =P(q₁ + q₂)q₂ - TC(q₂) (6,17)

Пусть кривая отраслевого спроса представлена линейной функцией:

Р = а – b Q,

где Q = q₁+ q₂,

тогда

П₁ = (a - bq₁ - bq₂) q₁– c q₁= a q₁ – b q₁² - b q₂q₁ – c q₁ (6.18)

П₂ = (a – bq₂ - bq₁) q₂– c q₂ = a q₂ - bq₂² - bq₂q₁ – c q₂ (6.19)

Необходимое условие максимизации прибыли каждого дуополиста при заданном (неизменном) выпуске другого:

∂ П₁ / ∂q₁ = a - 2bq₁ - bq₂ - c = 0 (6.20)

∂ П₂ / ∂q₂ = a - 2bq₂ - bq₁ - c = 0 (6. 21)

Отсюда

q₁ = ((a – c) / 2b) – q₂ / 2 =-1/2q₂+(а-с)/2b (6.22)

q₂ = ((a – c) / 2b) – q₁ / 2 =-1/2q₁+(а-с)/2b (6.23)

Эти уравнения характеризуют кривые реакции фирм 1 и 2, показывающие те объемы выпуска каждой из фирм, которые приносят ей максимальные значения прибыли при заданном выпуске соперника.

Равновесные значения выпуска для фирм можно получить, решив систему уравнений (6.13) и (6.14).

Поскольку функции реакции симметричны, q₂* =q₁*, получим:

q₁*= q₂*= (а-с) / 3b. (6.24)

Проверим выполнение достаточного условия максимизации прибыли второго порядка, определив знак вторых производных функций прибыли (6.9) и (6.10):

∂ П₁ ²/ ∂q₁² = - 2b < 0 (6.25)

∂ П₂ ²/ ∂q₂² = - 2b < 0. (6.26)

Поскольку условие второго порядка выполняется, равновесные объемы q₁* и q₂* действительно максимизируют прибыль каждого дуополиста

В сумме равновесный отраслевой выпуск при дуополии Курно составит:

Q* =2(а-с) / 3b,(6.27)

Равновесная ценав отрасли:

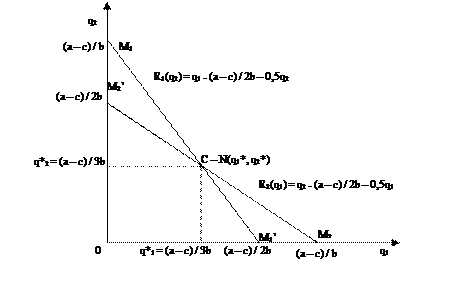Р* = (а + 2с) / 3 (6.28)

	Рис.6.10.Равновесие дуополии Курно

В условии совершенной конкуренции при тех же издержках и кривой спроса равновесный отраслевой выпуск был бы равен Q*=(а-с)/b., а цена Р* = с.

В условиях чистой монополии равновесный выпуск Q*,производимый при MR = а - 2bQ = с, равнялся бы Q*=(а-с)/2b, а равновесная цена Р* = (а + с) / 2.

.Вывод: при прочих равных условиях отраслевой выпуск в дуополии Курно оказывается выше монопольного, но меньше конкурентного, а равновесная цена в отрасли ниже монопольной, но выше конкурентной..

При помощи изопрофит (линий равной прибыли) и кривых реакции фирм 1 и 2 проиллюстрируем равновесный исход в модели дуополии Курно, производящей однородную продукцию. Форма изопрофит определяется видом функции спроса. Поскольку в нашем примере функция спроса линейна, так что, при постоянном значении прибыли и заданной величине выпуска соперника изопрофитные линии фирмы 1 и фирмы 2 представлены параболами., ветви которых обращены вниз (поскольку функция прибыли является квадратной функцией (6.18, 6.19.). Ветви изопрофит первой фирмы обращены к оси q_l,, а ветви изопрофит второй фирмы обращены к оси q₂.

Кривые, принадлежащие семейству изопрофит обладают следующими свойствами(рис. 6.11):

1) Они вогнуты к оси, по которой откладывается объем выпуска фирмы. Изопрофиты фирмы 1 вогнуты к оси q₁, a изопрофиты фирмы 2 к оси q₂). Вогнутость определяется реакцией фирмы на решение о выпуске, принятое соперником. Степень реакции должна быть такой, чтобы уровень прибыли фирмы остался неизмененным.

Рис. 6.11. Семейства изопрофит и кривые реагирования дуополистов Курно для фирм-производителей однородных товаров.

Предположим, что фирма 2 производит q¹₂ (см. рис.6.12). Тогда фирма 1 будет получать прибыль П₁¹, производя или q^h₁, или q^g₁.

Здесь возможны два варианта развития событий.

а) если фирма 2 увеличивает свой выпуск до q²₂. то фирма 1, стремясь сохранить уровень прибыли П₁¹ сократить выпуск до q^f₁.

Так как фирма 1 изначально выбрала больший из двух возможных выпусков q^g_1, то при увеличении производства фирмой 2, фирма 1 должна сократить свое. Иначе это приведет к росту объема предложения на рынке в целом, снижению рыночной цены и, в результате, уменьшению прибыли фирмы 1.

Это произойдет из-за того, что большой объем производства фирмы 1, скорее всего, соответствует области неэластичного спроса. Поэтому снижение рыночной цены приведет к снижению совокупной выручки ТR. При этом может оказаться, что при большом объеме производства перестает действовать положительная отдача от масштаба. Поэтому сокращение производства приведет к снижению совокупных издержек ТС и, тем самым, позволит сохранить неизменный размер прибыли.

Фирма 1 в ответ на увеличение производства фирмы 2 будет сокращать свой выпуск до уровня q^e₁, сохраняя тем самым неизменным уровень прибыли П₁¹.

б) если бы фирма 1 исходно выбрала бы небольшой объем производства q^h₁, при котором спрос является эластичным, то снижение рыночной цены из-за увеличения общего рыночного предложения, которое произойдет в результате роста производства на фирме 2, заставит фирму 1 производить больше. При этом фирма 1 сможет сохранить свою прибыль П₁¹, лишь увеличив свой выпуск до q^e₁. Это возможно потому, что при малых объемах действует положительная отдача от масштаба и рост производства фирмы 1 может приводить к снижению совокупных издержек ТС.

Рис. 6.12. Изопрофитная линия фирмы 1

2). Чем дальше от оси выпуска фирмы расположены ее изопрофиты, тем меньший уровень прибыли они характеризуют. Максимум прибыли каждой из фирм, равный монопольной прибыли, достигается на осях, в точках M₁ и M₂, т.е. там, где соперник ничего не производит. (см. рис.6.12).

Для фирмы 1 оптимальный объем производства определяется точкой касания линии уровня выпуска фирмы 2, параллельной оси выпуска фирмы 1, и самой низкой из возможных (при данном выборе фирмы 2) изопрофиты фирмы 1. Эта точка будет высшей точкой самой низкой из достижимых изопрофит.

фирмы 1.

3) Высшие точки изопрофит фирм-дуополистов смещены к оси выпуска соперника (см. рис. 6.11). Для фирмы 1 они смещены влево (для фирмы 2 — вправо), поскольку чем выше выпуск одной из фирм (фирмы-соперника), тем меньше выпуск другой и тем меньше прибыль последней.

Соединив высшие точки изопрофитных кривых получим кривые реакции фирм-дуополистов. Кривые реакции представляют собой геометрическое место точек максимумов прибыли одного дуополиста при заданном выпуске другого (R1(q₂) и R(q₁) (рис.6.11).

Точка пересечения кривых реакции (т.С) определяет равновесие по Курно (рис. 6.13). В этой ситуации у дуополистов отсутствует стимул к изменению своего положения, т.е достигнута ситуация равновесия по Нешу.

(Напомним, что тип рыночного равновесия, в котором ни одна из фирм не хочет в одностороннем порядке изменить свой выбор, поскольку он является наилучшим ответом на поведение соперников, называется равновесием по Нэшу).

Равновесие в дуополии Курно устойчиво и стабильно, если кривая реакции фирмы 1 круче кривой реакции фирмы 2 (рис. 6.13).

Рис. 6.13. Устойчивость равновесия в дуополии Курно

Если фирма 1 произведет q¹₁ меньше q₁*, то фирма 2, считая, что фирма 1 по-прежнему будет выпускать q¹₁, произведет q¹₂.

Тогда фирма 1, считая, что фирма 2 неизменно будет производить q¹₂, выпустит q²₁. На это фирма 2 отреагирует сокращением собственного выпуска до q₂². Изменения в производстве фирм в соответствии с их функциями реакции будет происходить до тех пор, пока они не окажутся в точке равновесия Курно-Неша, точке C- N, которое будет достигнуто при объеме выпуска первой фирмы q₁* и объеме выпуска первой фирмы q₂*.

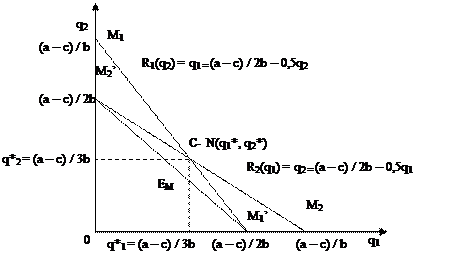6.14. Кривые реагирования в модели Курно и контрактная кривая

Максимизация прибыли фирмой-дуополистом Курно не приводит к максимизации прибыли отрасли в целом..

Докажем это. Построим контрактную кривую, которая соединит точки касания изопрофит (кривая Е₁Е₂ на рис. 6.15, 6.14).

6.15. Изопрофиты и контрактная кривая

Контрактная кривая соединяет все точки касания изопрофит, т.е. оптимальные точки, характеризующие максимальную совокупную прибыль отрасли.

В любой точке отрезка Е₁Е₂ контрактной кривой, отсекаемого изопрофитными линиями, проходящими через C -N, совокупная отраслевая прибыль выше, чем в точке C-N. При этом в точке Е₁ фирма 1имеет ту же прибыль (П₃¹) что и в точке С-N, а фирма 2 — большую (П₂²> П₃²); в точке Е₂ фирма 2 имеет ту же прибыль (П₃²), что и в точке C-N, а фирма 1 — большую (П₂¹ > П₃¹); в точках же между Е₁ и Е₂ обе фирмы будут получать прибыль большую, чем в C^N. Парадокс модели Курно заключается в том, что фирмы в итоге приходят к неоптимальному, с позиции максимизации совокупной прибыли, результату.

Объяснить этот парадокс можно, вспомнив о тех допущениях, которые мы делали при построении модели. Мы считали, что фирмы имеют возможность лиши однократного взаимодействия, поэтому они могут учиться на прошлом опыте. Каждая из фирм действует независимо — не зная о том, что соперник руководствуется тем же самым предположением в отношении ее поведения, что и она — в отношении него.

Модель Курно в случае n фирм.

Теперь рассмотрим олигополистическую отрасль, в которой действуют nфирм с такими же функциями издержек, что и в случае дуополии.

В случае nфирм Q = q₁ +... + q_i +... + q_n,функция прибыли для i-й фирмы:

П_i= (а - bQ)q_i - ТС-= (а – bq₁ -... – bq_i-... – bq_n) bq_i -TCi

Необходимое условие максимизации прибыли:

а – bq₁ -... – bq_i -... - bq_n - с = 0. (6. 28)

Отсюда:

q_i = ((а-с) / 2b) – (q₁ + … + q_{i –1} + q_{i +1} + … + q_n) / 2 (6.29)

Поскольку функции реакции у всех фирм симметричны и значения выпусков, максимизирующих прибыль, одинаковы (q₁= …= q_i-=... = q_n),можно заменить каждое из (n - 1) значений выпуска в уравнении (6.29) на q_i,получив:

q_i = ((а-с) / 2b) –((n - 1) q_i / 2). (6.30)

откуда

q_i = (а-с) / b(n + 1) (6.31)

Равновесный отраслевой выпуск в случае nфирм составит:

Q* = n q_i* = (n(а-с) / b) •(n / (n + 1)) (6.32)

По мере увеличения числа фирм nв олигополии Курно отраслевой выпуск будет расти (величина n / (n + 1) тоже растет, стремясь к 1), а цена — снижаться, т.е. исход в пределе, при n→∞, будет бесконечно приближаться к совершенно конкурентному. (См. Приложение 1)

Модель Чемберлина

В Модели Чемберлина (1956г.) в отличие от модели Курно дуополист предполагает, что уровень выпуска конкурента изменяется в ответ на его решения. В итоге дуополисты, не вступая в тайный сговор, выберут для себя наиболее выгодные для себя решения (рис.6.16). Примем, что МС₁=МС₂=0

Первый шаг. Пусть первая фирма ведет себя как монополист. Максимизируя прибыль она выберет объем производства и цену:

q₁=Q_m=(а-с)/2b (6.33)

Р_m==(а+с)/2 (6.34)

При этом прибыль составит:

П₁= (а – с)²/4 bq (6.35)

Рис. 6.16 Модель олигополии Чемберлина (простейшая версия)

Второй шаг. Вторая фирма, принимая решение, исходит уже из остаточной функции спроса АD’, считая что выпуск первой фирмы не изменится. Вторая фирма на остаточном спросе также принимает решение как монополист. Остаточную функцию спроса можно рассмотреть как функцию рыночного спроса, но только в новой системе координат, смещенной по отношению к первоначальной на q₁. Уравнение остаточной функции спроса:

Р’=(а+с)/2-bq₂ (6.36)

Максимизируя прибыль вторая фирма будет производить ровно половину от монопольного выпуска первой фирмы:

q₂=(а-с)/4b (6.37)

В итоге при снижении цены до:

Р=(а+3с)/4 (6.38)

отраслевой объем выпуска составит:

Q=3(а-с)/4b (6.39)

Поскольку уже в результате второго шага рыночная цена снизилась, прибыль первой фирмы составит всего лишь половину от первоначальной монопольной прибыли:

П₁= (а – с)²/8 b, (6.40)

а у второй фирмы – еще меньше:

П₂= (а – с)²/16 b. (6.41)

Третий шаг. Первая фирма, понимая, что вторая фирма реагирует на ее действия, сокращает свой объем производства вдвое (на размер выпуска конкурента), желая оставить монопольную цену Р_m=(а+с)/2.

Четвертый шаг. Вторая фирма, понимая, что ей выгоднее принять условия, предложенные первой фирмой, оставит свой объем производства неизменным, но будет продавать его по цене Р_m=(а+с)/2, которая выше его первоначальной цены.

В результате дуополисты поделят рынок поровну:

q_i = q₂ = (а-с)/4b (6.42)

и получат равную прибыль

П₁= П₂= (а – с)²/8 b, (6.43)

разделив монопольную прибыль между собой поровну.

Поскольку мы предположили существование линейной функции спроса р=а-2bQ и однородность выпускаемой продукции (поэтому q₁=q₂=q), то функция спроса примет вид:

р=а-2bq (6.44)

А поскольку мы считали, что издержки равны, то функция прибыли:

П= а q– 2bq^{2 -}сq, (6.45)

Необходимое условие максимизации прибыли:

dП/dq= а – 4bq - с=0 (6.46)

Достаточное условие максимизации прибыли

d²П/d²q= – 4b<0 (6.47)

Вывод: если выполняются предпосылки о равных издержках и однородности продукции, то фирмы в модели Чемберлина не вступая в тайный сговор, установят на рынке монопольную цену.

Модель олигополии Стэкльберга

Модель немецкого экономиста Генриха фон Стэкльберга (1934 г) называют моделью лидерства по объему выпуска, или моделью асимметричной дуополии. Модель Стэкльберга позволяет проанализировать взаимодействие фирм как лидеров и последователей.

Фирма считает себя лидером по объему выпуска, если ей удается первой принять решение об уровне выпуска. Лидер в модели Стэкльберга знает, что его соперник ведет себя по Курно, знает его функцию реакции и учитывает ее в собственной функции прибыли, которую он при этом максимизирует как монополист.

Последователь в модели Стэкльберга понимает, что конкурент является лидером, поэтому ведет себя так же, как и в модели Курно: максимизирует свою прибыль, считая выпуск соперника заданным (рассматривает выпуск фирмы –лидера в качестве экзогенного параметра, т.е. принимает решение при нулевой предполагаемой вариации λ= ∂q₁ / ∂q₂=0).

Модель Стэкльберга - модель однократного взаимодействия, в которой на роль лидера может в равной мере претендовать любой из дуополистов.

Поскольку в данной модели мы делаем те же предпосылки, что и в модели Курно, поэтому поведение дуополистов Стэкльберга характеризуют такие же изопрофиты и кривые реакции, как и у дуополистов Курно.

Рассмотрим случай линейной кривой спроса и равных предельных издержек у дуополистов (рис. 6.17)

1) Пусть первая фирма является лидером, а вторая фирма – последователем. Поскольку лидер максимизирует прибыль, считая, что фирма-последователь будет принимать решения о выпуске в соответствии со своей кривой реакции (RF₂), то равновесие в отрасли будет достигнуто в точке касания кривой реакции (RF₂)и изопрофиты П₁⁰ фирмы 1 (рис. 6.15). Изопрофита П₁⁰ является самой низкой из доступных при данной кривой реакции второй фирмы. В точке (S₁^L) выпуск лидера, позволяющий получить ему максимальную прибыль с учетом функции реакции соперника, составит q₁^L.. Это равновесие представляет собой разновидность равновесия по Нэшу,

Фирма - последователь при этом будет иметь объем производства q^F₂ в соответствии со своей кривой реакции (RF₂).

Фирма 1, выступая в роли лидера в дуополии Стэкльберга в ситуации отраслевого равновесия получит большую прибыль, чем получила бы в роли дуополиста Курно, т.к. находится на более низкой изопрофите.

Фирма 2, выступая в роли последователя проигрывает в прибыли, поскольку находится на более высокой изопрофите, чем П₂⁰ (поскольку через точку S₁^L пройдет более высокая изопрофита фирмы 2).

Чтобы найти объем выпуска и цену, по которой фирма-лидер будет максимизировать свою прибыль при заданной реакции фирмы-последователя, подставим в уравнение прибыли лидера (6.18): П₁ = (a - bq₁ - bq₂) q₁– c q₁, вместо q₂ функцию реакции фирмы 2 (последователя) (6.23): q₂ = -(1/2)q₁+(а-с)/2b

тогда прибыль лидера:

П₁^L = [a – bq_i – b((-1/2q₁+(а-с)/2b] q₁ – с q₁ = aq₁ – bq_i ² + b q₁² /2- (а-с)/2b – с q_1,

откуда П₁^L = ((а-с)/2) q₁- bq₁² / 2. (6. 48)

Условие первого порядка для максимизации прибыли фирмы 1-лидера:

∂ П₁ / ∂q₁ = ((a – c) / 2)- bq₁ = 0 (6.49)

Отсюда находим:

q₁^L*= (a – c) / 2b. (6.50)

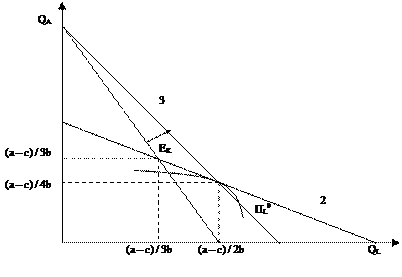Рис. 6.17. Равновесие в дуополии Стэкльберга

Таким образом, фирма-лидер1 производит такой же объем продукции, как и монополист.

Условия второго порядка также выполняется: -b<0, (т.к. само значение b>0),

Равновесный выпуск фирмы - последователя 2 найдем, подставив полученное значение выпуска лидера (6.50) в уравнение функции реакции фирмы 2 (6.23):

q₂^F* = - (a – c) / 4b + (a – c) / 2b = (a – c) / 4b (6.51)

Равновесный отраслевой выпуск в дуополии Стэкльберга получим, просуммировав выпуск фирмы-лидера 1 (6.50) и фирмы- последователя 2 (6.51):

Q*= q₁ + q₂ = 3(a – c) / 4b. (6.52)

Равновесную цену получим, подставив значение отраслевого выпуска (6.52) в функцию рыночного спроса:

P* = a - b ' 3(a – c) / 4b = (a + 3c) / 4 (6.53)

Прибыль лидера составит:

П₁= (а –с)²/8b (6.54)

Прибыль последователя: П₁= (а –с)²/16b (6.55)

Вывод: преимущество первого хода позволяет фирме-лидеру получать прибыль в два раза большую, чем получит последователь. Поэтому последователь также хочет быть лидером (рис.6.17а).

2). Ситуация отраслевого равновесия по Стэкльбергу, если фирма 2 будет выступать в роли лидера, а фирма 1 в роли последователя представлена точкойS₂^L (рис.6.17.). Поскольку мы исходили из симметричных функций спроса и издержек, то результаты для ситуации, когда фирма 2 станет лидером, а фирма 1 последователем, будут такими же, что и в случае лидерства фирмы 1 и последователя фирмы 2 с той только разницей, что индексы в формулах будут изменены с q₁ на q₂.

3) В ситуации, когда обе фирмы претендуют на роль лидера, отраслевое равновесие в модели Стэкльберга не достигается. Тогда во избежании "ценовой войны" дуополисты должны будут договориться: либо о том, что кто из них все же станет лидером, либо создадут картель, который позволит максимизировать прибыль отрасли. (Значения прибыли, цены и объема выпуска лидера, последователя и отрасли попробуйте определить самостоятельно, см. т. В на рис. 6.17а). (См. Приложение 6.2)

(Подробнее о модели «борьба за лидерство» в кн.: А.Вурос, Н. Розанова «Экономика отраслевых рынков» М.,2000,- с.125-128).

На рис.6.17а в качестве итога рассмотрения моделей количественной дуополии представлены соотношения оптимальных объемов выпуска: модели Курно (т.К), модели Стакильберга (т.С₁, если лидер 1 фирма ит.С₂ – если лидер –2 фирма). Таким образом, в модели Стакильберга фирмы совместно производят объем производства больший, чем в модели Курно (рис. 6.17а).

q₁

Рис. 6. 17а.Равновесие в моделях количественной олигополии.

Дата добавления: 2014-11-18