
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные формулы. Раздел физики, в котором рассматриваются законы равновесия и движения жидких и газообразных тел, а также их взаимодействия с твердыми телами
|
|
|
|
Раздел физики, в котором рассматриваются законы равновесия и движения жидких и газообразных тел, а также их взаимодействия с твердыми телами, называется гидроаэромеханикой.
Характерным свойством жидких и газообразных тел является их текучесть, то есть малая сопротивляемость деформации сдвига: если скорость сдвига стремится к нулю, то силы сопротивления жидкости или газа этой деформации также стремятся к нулю. Иными словами, жидкие и газообразные тела не обладают упругостью формы — они легко принимают форму того сосуда, в котором находятся. Вследствие этого (закон Паскаля): внешнее давление, производимое на жидкость или газ, передается ими во все стороны равномерно.
Основным методом описания движения жидкости в гидроаэродинамике является метод Эйлера, состоящий в задании зависимости значений вектора υ скорости течения жидкости в различных точках пространства от координат этих точек (х, у, z) и времени t:
| υ = f (r, t) | (2.1) |
или
| υx = f1 (x, y, z, t) υy = f2 (x, y, z, t) υz = f3 (x, y, z, t) | (2.2) |
где r = xi + yj + zk - радиус-вектор, проведенный из начала координат в рассматриваемую точку; i, j и k - единичные векторы (орты осей координат), υx, υy и υz - проекции вектора υ на оси координат.
Течение жидкости называется установившимся, или стационарным, если скорость жидкости в каждой точке пространства, занятого жидкостью, не изменяется с течением времени, то есть υ не зависит от t: υ = f (r). В случае неустановившегося течения v зависит также и от времени t.
Рассмотрим участок элементарной струйки жидкости, ограниченной двумя произвольно выбранными нормальными сечениями 1и 2,площади которых равны dS 1 и dS2(рис. 2.1).

Рис. 2.1.
Участок элементарной струйки жидкости, ограниченной двумя произвольно выбранными нормальными сечениями 1и 2,площади которых равны dS 1 и dS2
Скорости жидкости в этих сечениях обозначим через v1 и v2. Если течение жидкости установившееся, то масса жидкости, заключенной в участке струи между сечениями 1и 2, не зависит от времени. Следовательно, масса dm1=ρ1v1ּdS1 жидкости, поступающей в рассматриваемый участок за единицу времени сквозь сечение 1, равна массе dm2 = ρ2v2 ּ dS2 жидкости, вытекающей из этого участка за то же время сквозь сечение 2:
| ρ1v1 ּdS1 = ρ1v2 ּdS2 | (2.3) |
Выделим мысленно часть идеальной несжимаемой жидкости, которая в некоторый момент времени tзаполняет участок элементарной струи, ограниченный нормальными сечениями 1и 2(рис.2.2).
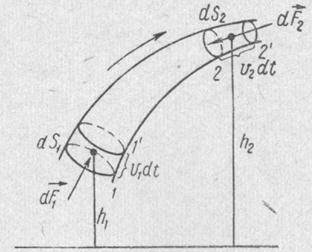
Рис. 2.2.
Элементарный участок струи, ограниченный нормальными сечениями 1 и 2
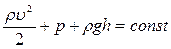
| (2.4) |
Это уравнение впервые было получено Д. Бернулли и называется уравнением Бернулли. Оно, как видно из его вывода, является выражением закона сохранения энергии применительно к установившемуся течению идеальной несжимаемой жидкости.
В случае горизонтальной струи (например, при течении жидкости в горизонтальной трубе) величина hпостоянна и уравнение Бернулли принимает более простой вид:
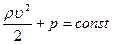
| (2.4‘) |
Величина р называется статическим давлением, 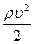 - скоростным, или динамическим, напором, а р0 = р +
- скоростным, или динамическим, напором, а р0 = р + 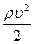 — полным давлением.
— полным давлением.
Динамический напор равен:
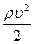 =ρ×g×ΔH, =ρ×g×ΔH,
| (2.5) |
где ΔH — разность уровней жидкости в трубках а и Ь соответственно полного и статического давлений.
|
|
|
|
|
Дата добавления: 2014-11-18; Просмотров: 820; Нарушение авторских прав?; Мы поможем в написании вашей работы!