
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства плотности вероятностей
f1). Плотность вероятностей 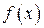 является функцией неотрицательной:
является функцией неотрицательной:
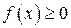 для любого
для любого 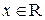 .
.
▲ Поскольку функция распределения 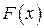 является функцией неубывающей, то ее производная
является функцией неубывающей, то ее производная 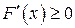 . Поэтому свойство следует из равенства (2.5) ■.
. Поэтому свойство следует из равенства (2.5) ■.
f2). Площадь под графиком плотности вероятностей 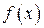 равна единице:
равна единице:
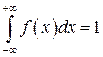 - условие нормировки.
- условие нормировки.
▲ Из представления (2.3) следует, что 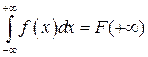 , а в соответствии со свойством F2) функции распределения
, а в соответствии со свойством F2) функции распределения  ■.
■.
f3). Вероятность попадания непрерывной случайной величины 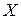 в интервал
в интервал 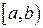 определяется как интеграл от плотности вероятностей по этому интервалу: для любых
определяется как интеграл от плотности вероятностей по этому интервалу: для любых 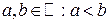
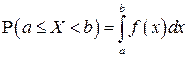 . (2.6)
. (2.6)
▲ Поскольку в соответствии со свойством F6) функции распределения 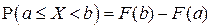 , то данное свойство непосредственно вытекает из представления (2.3):
, то данное свойство непосредственно вытекает из представления (2.3):
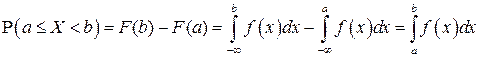 ■.
■.
Следствие. Для непрерывной случайной величины 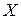
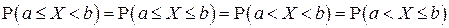
и все вероятности определяются с помощью интеграла (2.6).
Графическая иллюстрация функции распределения и плотности вероятностей непрерывной случайной величины.
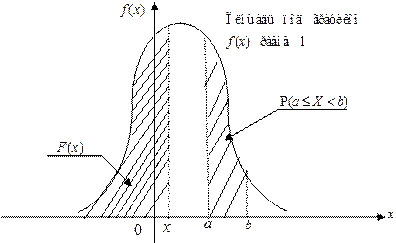
2.5. Важнейшие непрерывные случайные величины
1. Равномерная случайная величина.
 Говорят, что непрерывная случайная величина
Говорят, что непрерывная случайная величина 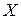 имеет равномерный закон распределения (равномерное распределение) на отрезке
имеет равномерный закон распределения (равномерное распределение) на отрезке 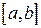 , если множество ее возможных значений
, если множество ее возможных значений 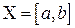 , а плотность вероятностей постоянна на этом отрезке:
, а плотность вероятностей постоянна на этом отрезке:
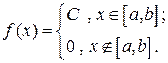
Константа С при этом однозначно определяется из условия нормировки:
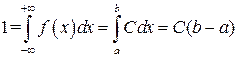 , то есть
, то есть  .
.
Таким образом, равномерно распределенная случайная величина имеет плотность вероятностей:
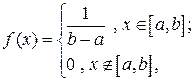
и для нее используется сокращенное обозначение: 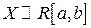 .
.
Найдем функцию распределения 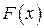 случайной величины
случайной величины 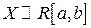 .
.
Для этого рассмотрим три случая:
а) если 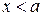 , то
, то 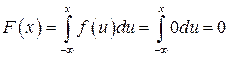 ;
;
б) если 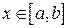 ,то
,то 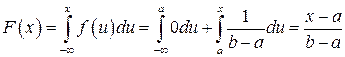 ;
;
в) если 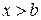 , то
, то 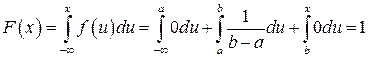 .
.
Окончательно имеем:
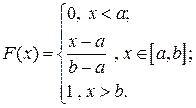
Графики плотности вероятностей и функции распределения случайной величины 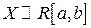 имеют вид:
имеют вид:
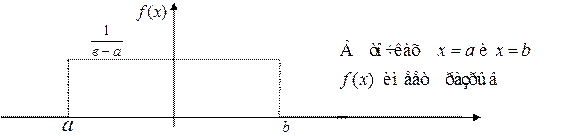
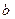
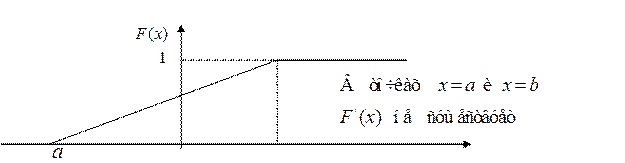
2. Показательная (экспоненциальная) случайная величина.
 Говорят, что непрерывная случайная величина
Говорят, что непрерывная случайная величина 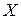 имеет показательный закон распределения (показательное, экспоненциальное распределение), если множество ее возможных значений
имеет показательный закон распределения (показательное, экспоненциальное распределение), если множество ее возможных значений 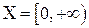 , а плотность вероятностей имеет вид:
, а плотность вероятностей имеет вид:
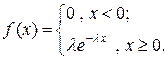
Число 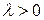 называется параметром показательного закона распределения, а для показательной случайной величины используется сокращенное обозначение:
называется параметром показательного закона распределения, а для показательной случайной величины используется сокращенное обозначение: 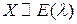 .
.
Проверим условие нормировки:
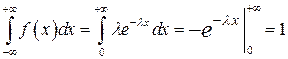 при любом
при любом 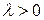 .
.
Найдем функцию распределения случайной величины 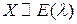 .
.
Для этого рассмотрим два случая:
а) если 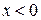 , то
, то 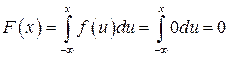 ;
;
в) если 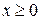 , то
, то 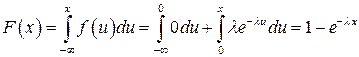 .
.
Окончательно имеем:
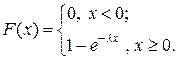
Графики плотности вероятностей и функции распределения случайной величины 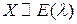 имеют вид:
имеют вид:
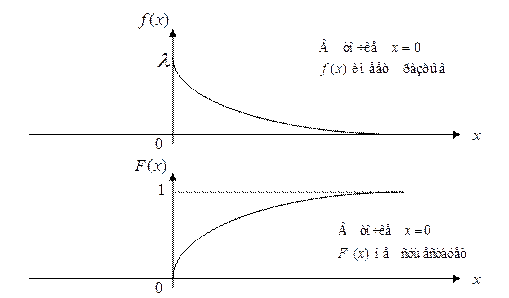
3. Нормальная (гауссовская) случайная величина.
 Говорят, что непрерывная случайная величина
Говорят, что непрерывная случайная величина 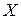 имеет нормальный закон распределения (нормальное, гауссовское распределение) с параметрами
имеет нормальный закон распределения (нормальное, гауссовское распределение) с параметрами 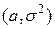 , если множество ее возможных значений
, если множество ее возможных значений 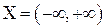 , а плотность вероятностей имеет вид:
, а плотность вероятностей имеет вид:
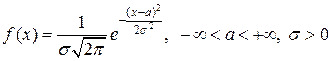 .
.
Сокращенное обозначение нормальной случайной величины:
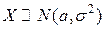 .
.
Кривая плотности вероятностей имеет симметричный вид относительно прямой  и имеет максимум в точке
и имеет максимум в точке  .
.
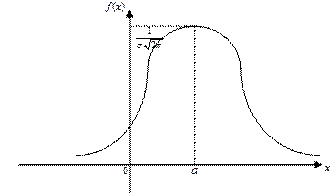
Проверим условие нормировки:
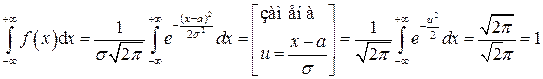
для любых значений параметров а и 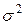 (при этом использовался известный в анализе факт, что
(при этом использовался известный в анализе факт, что 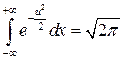 - интеграл Пуассона).
- интеграл Пуассона).
В зависимости от изменения параметров плотность вероятностей нормального закона распределения меняется следующим образом.
Если параметр 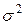 фиксирован, то при изменении а кривая
фиксирован, то при изменении а кривая 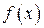 , не изменяя своей формы, просто смещается вдоль оси абсцисс. Таким образом, параметр а является параметром сдвига (положения). Также параметр а характеризует среднее значение случайной величины.
, не изменяя своей формы, просто смещается вдоль оси абсцисс. Таким образом, параметр а является параметром сдвига (положения). Также параметр а характеризует среднее значение случайной величины.
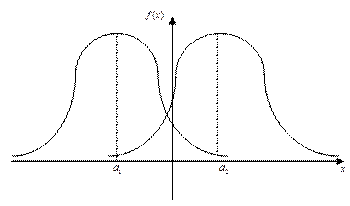
Изменение 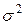 при фиксированном а равносильно изменению масштаба кривой
при фиксированном а равносильно изменению масштаба кривой 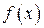 по обеим осям: при увеличении
по обеим осям: при увеличении 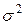 плотность вероятностей становится более плоской, растягиваясь вдоль оси абсцисс; при уменьшении
плотность вероятностей становится более плоской, растягиваясь вдоль оси абсцисс; при уменьшении 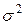 - вытягивается вверх, одновременно сжимаясь с боков (эффект действия условия нормировки). Таким образом, параметр
- вытягивается вверх, одновременно сжимаясь с боков (эффект действия условия нормировки). Таким образом, параметр 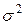 является параметром масштаба.
является параметром масштаба.
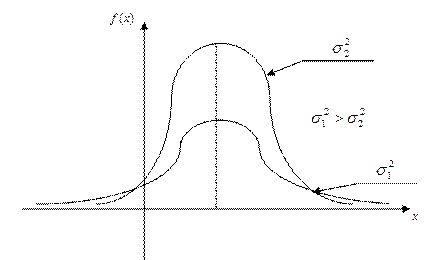
Также параметр 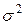 характеризует степень разброса значений случайной величины около среднего значения а в следующем смысле. Чем меньше
характеризует степень разброса значений случайной величины около среднего значения а в следующем смысле. Чем меньше 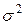 , тем больше при фиксированном
, тем больше при фиксированном 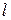 вероятность вида
вероятность вида 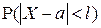 , как площадь под плотностью вероятностей или, другими словами, тем при меньшем
, как площадь под плотностью вероятностей или, другими словами, тем при меньшем 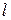 можно получить заданную вероятность вида
можно получить заданную вероятность вида 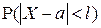 . Это означает, что при уменьшении
. Это означает, что при уменьшении 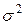 значения случайной величины
значения случайной величины 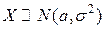 более плотно группируются около а, то есть степень разброса значений случайной величины около среднего значения а меньше.
более плотно группируются около а, то есть степень разброса значений случайной величины около среднего значения а меньше.
Если 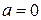 и
и 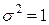 , то нормальный закон распределения называется стандартным, его плотность вероятностей имеет вид:
, то нормальный закон распределения называется стандартным, его плотность вероятностей имеет вид:
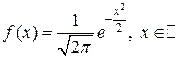
и называется функцией Гаусса.
Функция распределения случайной величины 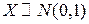 имеет вид:
имеет вид:
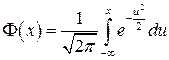
и не выражается в элементарных функциях. Функцию 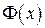 называют функцией Лапласа (или интегралом вероятностей).
называют функцией Лапласа (или интегралом вероятностей).
Геометрическая иллюстрация.
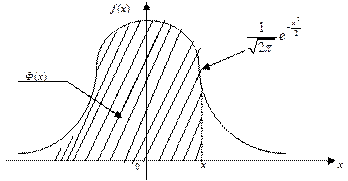
Свойства функции Лапласа 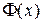 :
:
1. 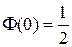 ;
;
2. 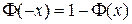 для
для 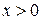 .
.
Значения функции Лапласа 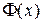 для
для 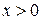 табулированы.
табулированы.
Функция распределения случайной величины 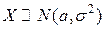 также выражается через функцию Лапласа
также выражается через функцию Лапласа 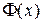 :
:
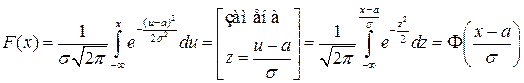 .
.
Вероятность попадания случайной величины 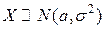 в заданный интервал
в заданный интервал 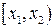 определяется по формуле:
определяется по формуле:
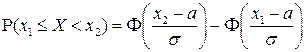 .
.
Наиболее просто выражается через функцию Лапласа вероятность попадания случайной величины 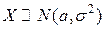 в интервал длины
в интервал длины 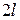 , симметричный относительно точки
, симметричный относительно точки  :
:
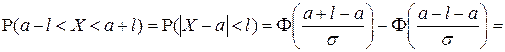
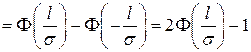 .
.
Далее, если положить 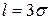 и учесть, что
и учесть, что 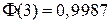 , то получаем:
, то получаем:
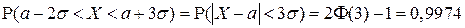 .
.
Полученный результат носит название «Правило трех сигма». Он означает, что «практически все» значения случайной величины 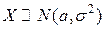 находятся внутри интервала
находятся внутри интервала  в том смысле, что вероятность случайной величине
в том смысле, что вероятность случайной величине 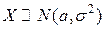 принять значение, не принадлежащее этому интервалу, пренебрежимо мала (
принять значение, не принадлежащее этому интервалу, пренебрежимо мала (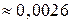 ).
).
Геометрическая иллюстрация «Правила трех сигма».
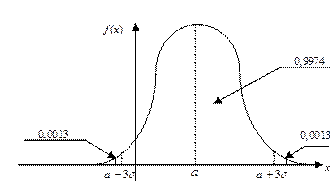
Нормальный закон распределения очень распространен и имеет чрезвычайно большое значение для практики. В этом мы убедимся, когда познакомимся с центральной предельной теоремой.
5. Случайная величина, имеющая закон распределения Коши.
 Говорят, что непрерывная случайная величина
Говорят, что непрерывная случайная величина 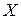 имеет закон распределения Коши, если множество ее возможных значений
имеет закон распределения Коши, если множество ее возможных значений 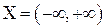 , а плотность вероятностей имеет вид:
, а плотность вероятностей имеет вид:
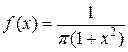 .
.
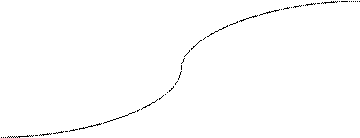
Функция распределения случайной величины, распределенной по закону Коши, имеет вид:
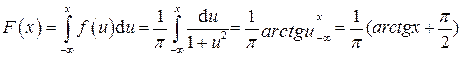 .
.
Графики плотности вероятностей и функции распределения случайной величины, распределенной по закону Коши, выглядят следующим образом:
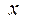

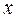
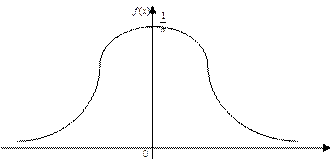
 | |||
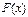 | |||

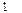

|
|
Дата добавления: 2014-11-18; Просмотров: 1705; Нарушение авторских прав?; Мы поможем в написании вашей работы!