Функцій

Теорема 10.5. Нехай функці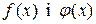ї і 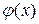із неперервні і диференційовані при всіх 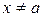з деякого околу точки а, в якому 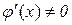, і нехай 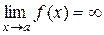і 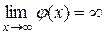. Тоді якщо існує границя

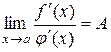, (10.5)

то існує границя 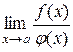і справедлива рівність

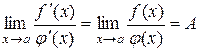. (10.6)

Доведення. В розглядуваному околі точки а виберемо два значення аргументу 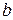і х таких, що 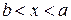(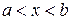). Тоді з теореми Коші слідує

,

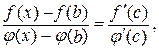де 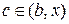або .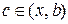

Зробимо тотожні перетворення в останній рівності:

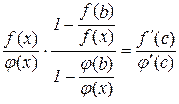
або

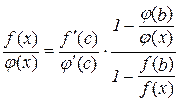. (10.7)

В (10.7) зафіксуємо 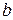і перейдемо до границі при :

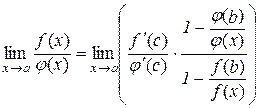(10.8)

Права частина рівності (10.8) дає:

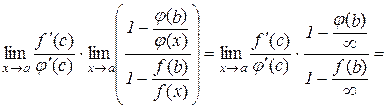
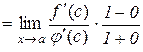. (10.9)

Таким чином, із (10.8), (10.9) отримуємо

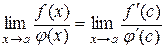. (10.10)

Права частина (10.10) є функцією значення с, яке залежить від вибору числа . Перейдемо в останній рівності до границі при . Так як при цьому, очевидно, 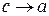, а ліва частина від 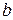не залежить, то отримаємо

.

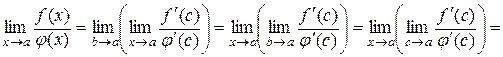
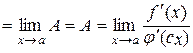Таким чином теорему доведено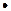

Наслідок 10.5.1. Рівність (10.6) справедлива і у випадку, коли .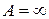

Дійсно, тоді 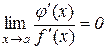і з останньої теореми слідує, що

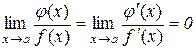або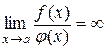

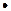
Наслідок 10.5.2. Доведена теорема легко поширюється на випадок .

Це слідує з наслідку 10.4.3

Приклад 10.5.

.

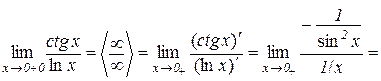
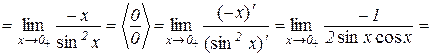
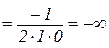Приклад 10.6.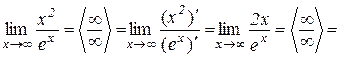

.

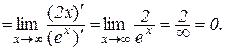За допомогою двох останніх теорем можна також розкривати невизначеності типу .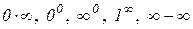

Приклад 10.7. Знайти границю

.

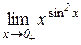Розв’язування. Нехай

,

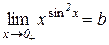тоді

.

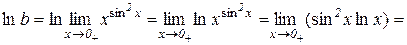
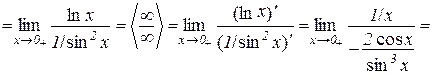
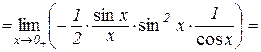
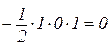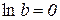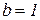Таким чином, або і .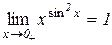

10.6. Формули Тейлора і Маклорена.

Припустимо, що в деякому околі точки а функція має всі похідні до (n+1) -го порядку. Знайдемо такий многочлен 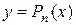, який в точці 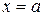набуває значення 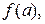, а всі його похідні до n -го порядку в цій точці рівні значенням відповідних похідних функції , тобто

(10.11)

Многочлен 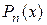будемо шукати у вигляді многочлена за степенями двочлена х-а:

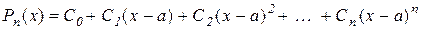. (10.12)

Коефіцієнти С₀, С₁ , С₂ , ..., С_n треба підібрати такими, щоб виконувалась умова (10.11).

Знайдемо похідні многочлена :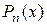

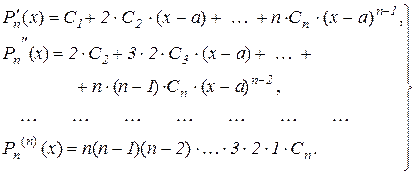(10.13)

З (10.11)–(10.13) маємо:

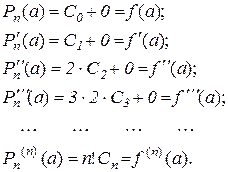
або

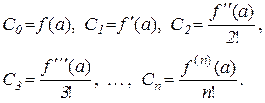(10.14)

Підставивши (10.14) в (10.12), отримаємо

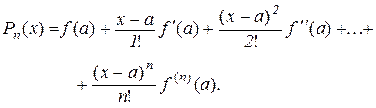
Нехай 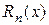– різниця між значеннями заданої функції і многочлена 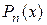, тобто 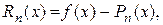, тоді

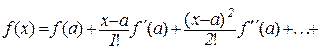
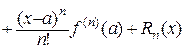. (10.15)

Означення 10.1. Функція 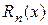називається залишковимчленом.

Проведемо оцінку залишкового члена. Для цього представимо його у вигляді

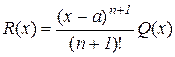, (10.16)

де 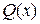– невідома функція, яку потрібно знайти.

Підставимо (10.16) в (10.15)

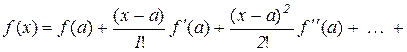
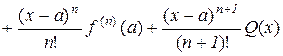, (10.17)

і розглянемо допоміжну функцію :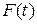

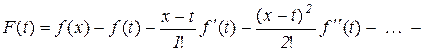
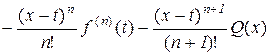, (10.18)

де t лежить в проміжку між а і х.

Знайдемо :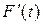

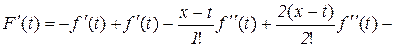
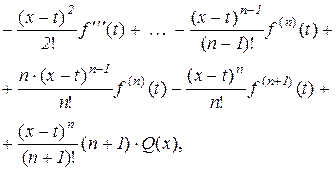
або після скорочення

. (10.19)

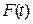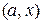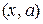Таким чином, з рівностей (10.17)–(10.19) слідує, що функція неперервна і диференційована на або та 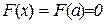, тобто для даної функції справедлива теорема Ролля: 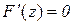, де z розміщене між а і х. З (10.19) отримуємо, що

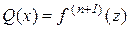
і залишковий член 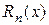можна подати у вигляді

,

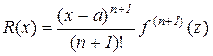який називають формою Лагранжа для залишкового члена.

Іколи застосовують запис 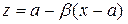, де 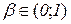, і залишковий член набирає вигляду

.

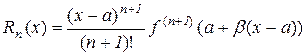Таким чином, ми отримали формулу

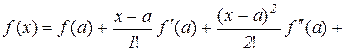
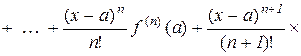
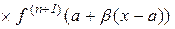, (10.20)

яка називається формулою Лагранжа для функції .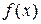

Частинний випадок формули (10.20) при 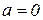, тобто

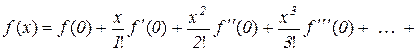
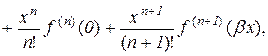(10.21)

називається формулою Маклорена.

10.7. Розклад за формулою Маклорена функцій

Дата добавления: 2014-11-18