Интерполяционная квадратурная формула

Пусть заданы узлы 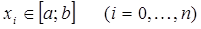квадратурной формулы (2). По подинтегральной функции 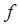и узлам 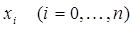построим интерполяционный многочлен Лагранжа

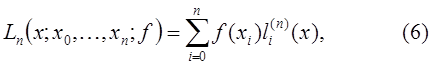
где , .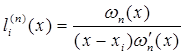

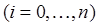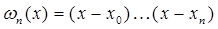Положив

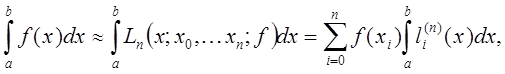
получим интерполяционную квадратурную формулу

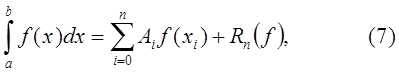
где

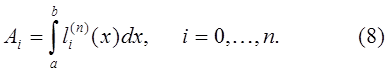
Таким образом, квадратурная формула (2) является интерполяционной, если её коэффициенты вычисляются по формуле (8).

Замечание 2. Коэффициенты интерполяционной квадратурной формулы зависят только от узлов 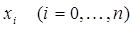и не зависят от подинтегральной функции .

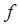Интерполяционная квадратурная формула (7)–(8) точна на многочленах степени 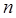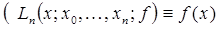, если 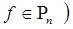. Очевидно, что если квадратурная формула (2) с 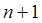узлами имеет алгебраический порядок точности не ниже 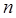, то она является интерполяционной.

Погрешность интерполяционной квадратурной формулы (7)–(8) имеет вид

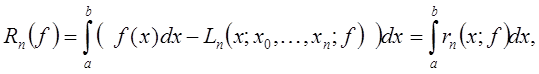
где 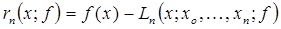- погрешность интерполяции.

Если 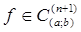, то

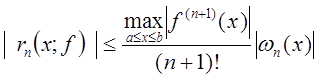
и, следовательно,

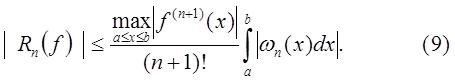
Часто оценку (9) заменяют более грубой

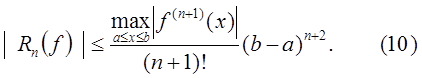
Теорема 2. Для сходимости квадратурного процесса (5), порожденного интерполяционной квадратурной формулой (7)-(8) с таблицей узлов : 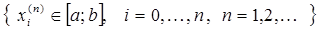, необходимо и достаточно, чтобы 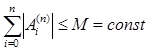для любого 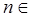N.

Действительно, для всякого многочлена 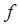степени 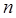имеем при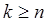 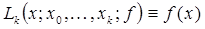и, следовательно, 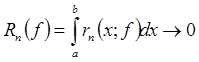при для любой функции 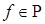, где 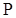- пространство многочленов, всюду плотное в 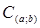. Утверждение теоремы 2 теперь немедленно следует из теоремы 1.

Для любой таблицы узлов 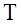: 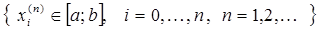, используя формулу (8), получаем

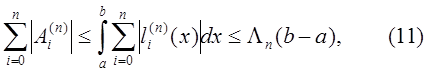
где 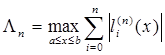- константа Лебега.

Замечание 3. При любом выборе узлов интерполяции 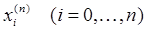имеет место (см. [4], стр. 118) неравенство С.Н.Бернштейна 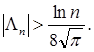Введем оператор 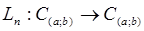, преобразующий функцию 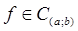в интерполяционный многочлен Лагранжа 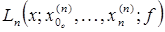. Оператор 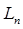- линейный и ограниченный. Нетрудно показать, что 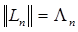. Из неравенства С.Н.Бернштейна и теоремы Банаха-Штейнгауса немедленно следует, что для любой таблицы узлов интерполяции 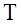: 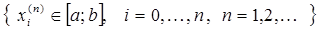найдется такая функция 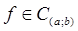, для которой последовательность интерполяционных многочленов 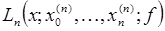неограниченно расходится.

Замечание 4. Расходимость интерполяционного процесса может вызвать осложнения в задаче вычисления интеграла. При неудачном выборе узлов квадратурный процесс (5), порожденный квадратурной формулой (7)–(8), будет расходящимся (сумма 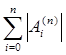может неограниченно расти).

Дата добавления: 2014-11-18