Правило трапеций

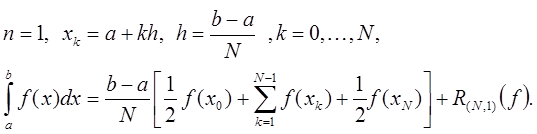
Если , то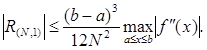

Правило Симпсона (парабол)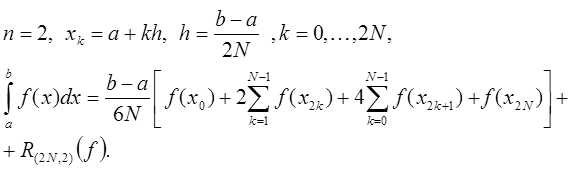

Если 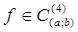, то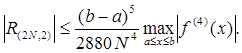

Замечание 5. Алгоритмы численного интегрирования, построенные на основе локально-интерполяционных квадратурных формул (25) имеют существенный недостаток – они насыщаемые. Насыщаемость проявляется в том, что асимптотическое представление погрешности формулы (25) имеет главный член. Отсюда следует неулучшаемость оценки погрешности, сколь бы ни была гладкой функция .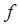

В зависимости от гладкости функции 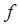можно выписать любое заданное число членов асимптотического ряда, в который разлагается погрешность 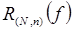. Рассмотрим конкретный пример – правило трапеций. Если 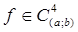, то для погрешности квадратурной формулы 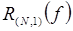имеет место представление

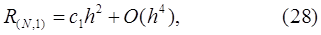
где 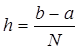и 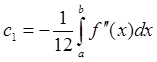не зависит от 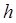. Из (28) и следует насыщаемость правила трапеций. Классом насыщения в данном случае является пространство .

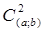Имеются простые способы преодоления дефекта локально интерполяционных квадратурных формул – их насыщаемости. Все они основаны на простом соображении, что у соответствующей линейной комбинации двух значений составной квадратурной формулы с различными, но кратными шагами, главный член погрешности исключается. Например, для правила трапеций в силу (28) 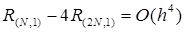, и мы получаем повышение порядка точности, если возьмем линейную комбинацию значений формулы для числа узлов 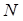и 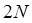соответственно с коэффициентами 1 и – 4.

Пусть погрешность локально-интерполяционной квадратурной формулы (25) представима в виде

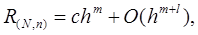
где 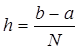и константа не зависит от 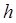. Тогда

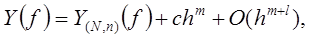
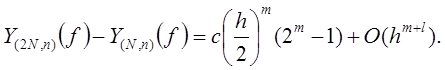
Отсюда получаем

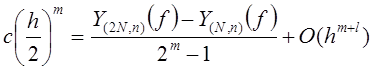
и, следовательно, с точностью до имеем

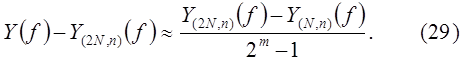
Если 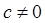, то

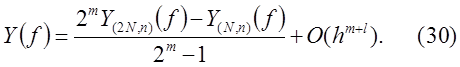
Вычисление приближенной оценки погрешности по формуле (29) называется правилом Рунге.

Число

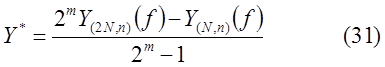
в (30) называется уточненным (экстраполированным) по Ричардсону приближенным значением интеграла 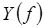(с погрешностью ).

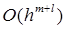Замечание 6. Используя этот прием, можно уничтожить и следующие члены асимптотического разложения погрешности квадратурной формулы. Однако целесообразнее применять квадратурные формулы, сразу приводящие к ненасыщаемым алгоритмам, например, составные формулы Гаусса. Отметим, что составные квадратурные формулы, основанные на формулах Гаусса с достаточно большим числом узлов, дают хорошие результаты как для очень гладких функций, так и для функций невыской гладкости.

Замечание 7. Каждая квадратурная формула рассчитывается на определенную гладкость подинтегральной функции. Например, для правила Симпсона погрешность 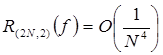, если 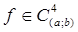. Если квадратурная формула имеет алгебраический порядок точности 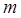, то при ее применении можно рассчитывать получить «малую погрешность» только в том случае, когда 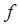имеет непрерывные производные до порядка, не меньшего 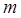. В противном случае погрешность вычисления интеграла может оказаться большой. Для увеличения порядка гладкости подинтегральную функцию 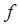представляют в виде двух слагаемых

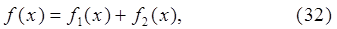
которые выбирают так, чтобы: 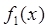содержала все особенности 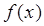или их главную часть и вычислялся точно; 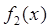должна иметь непрерывные производные порядка, большего 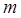, для того, чтобы интеграл 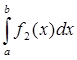можно было вычислить с достаточной точностью с помощью выбранной квадратурной формулы. Приемы разложения (32) для конкретных классов подинтегральных функций изложены в [3].

1.8. Задание. Вычислить интеграл 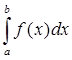с точностью 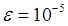, используя правило Симпсона и составную квадратурную формулу Гаусса с пятью узлами. Оценить погрешность используемых квадратурных формул и определить число частичных отрезков разбиения, необходимое для достижения заданной точности вычисления интеграла.

Замечание 8. Обычно для вычисления интеграла 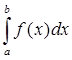с точностью 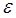используют итерационный процесс с последовательным удвоением числа 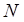частичных отрезков разбиения.

Если 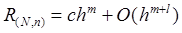, то условием останова процесса является выполнение неравенства

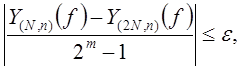
при этом интеграл вычисляется по формуле (31).

Варианты заданий

№ варианта		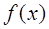		№ варианта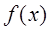
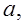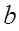
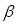
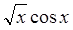
							0,1
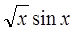
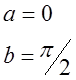
						0,2
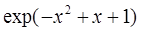
					0,3
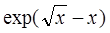
					0,4
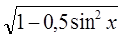
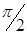
					0,5
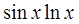
					0,6
					0,7
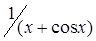
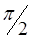
					0,8
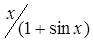
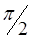
					0,9
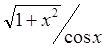
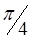
					1,0

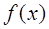
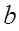
№ варианта				№ варианта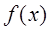
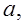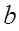
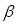
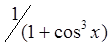
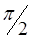
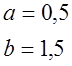
							0,1
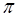
					0,2
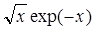
					0,3
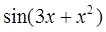
					0,4
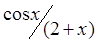
					0,5
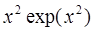
					0,6
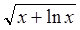
					0,7
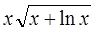
					0,8
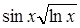
					0,9
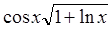
					1,0

Приложение. Для выполнения задания можно использовать следующие процедуры (на языке Паскаль):

1. Процедура simps, реализующая алгоритм правила Симпсона (парабол):

Procedure simps(a,b:real; var n:longint; var y:real);

{Входные параметры:

a – левый конец отрезка интегрирования;

b – правый конец отрезка интегрирования;

n - число частичных отрезков разбиения.

Выходные параметры:

y – значение интеграла.

Здесь f имя функции, вычисляющей значения подинтегральной функции.}

var

i:longint;

h,x:real;

begin

h:=(b-a)/n; y:=0; x:=a;

for i:=1 to n do

begin y:=y+f(x)+4*f(x+0.5*h)+f(x+h); x:=x+h end;

y:=y*h/6

end;

2. Процедура gauss, реализующая алгоритм составной формулы Гаусса с пятью узлами:

Procedure gauss(a,b:real; var n:word; var y:real);

{Входные параметры:

a – левый конец отрезка интегрирования;

b – правый конец отрезка интегрирования;

n - число частичных отрезков разбиения.

Выходные параметры:

y – значение интеграла.

Здесь f – имя функции, вычисляющей значения подинтегральной функции;

vec – одномерный массив (type vec=array[1..5]of real).}

var

i,j:word;

h,x,x1:real;

ag,xg:vec;

z:real;

begin

ag[1]:=0.2369268850; xg[1]:=-0.9061798459;

ag[2]:=0.4786286705; xg[2]:=-0.5384693101;

ag[3]:=0.5688888889; xg[3]:=0.0;

ag[4]:=ag[2]; xg[4]:=-xg[2];

ag[5]:=ag[1]; xg[5]:=-xg[1];

h:=(b-a)/n; z:=0; x1:=a+0.5*h;

for j:=1 to n do

begin

for i:=1 to 5 do

begin x:=x1+0.5*h*xg[I]; z:=z+ag[i]*f(x); end;

x1:=x1+h

end;

y:=z*0.5*h

end;

Дата добавления: 2014-11-18