Сходящиеся формулы численного дифференцирования

Пусть 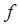гладкая на некотором интервале D вещественной прямой R функция и требуется вычислить производную . Построим сетку Рассмотрим формулу численного дифференцирования

где R, .

Разность

называется погрешностью формулы численного дифференцирования (36).

Формула численного дифференцирования (36) называется сходящейся, если при 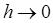для любой функции 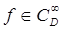(в любой точке гладкости функции ).

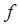Будем говорить, что формула (36) аппроксимирует 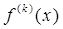с порядком (имеет 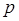- ый порядок точности), есл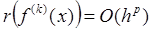и при .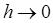

Функцию комплексного переменного 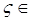С вида

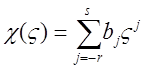
назовем характеристической функцией (символом) формулы численного дифференцирования (36).

Теорема 5. Формула численного дифференцирования (36) является сходящейся тогда и только тогда, когда ее характеристическая функция 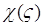представима в виде

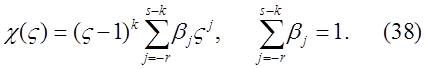
Замечание 11. В представлении (38) характеристической функции сходящейся формулы численного дифференцирования множитель

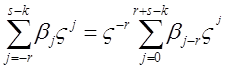
имеет корней; они называются характеристическими числами сходящейся формулы численного дифференцирования (характеристические числа отличны от 1).

Для построения формулы численного дифференцирования, имеющей 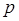- ый порядок точности, можно воспользоваться методом неопределенных коэффициентов.

Теорема 6. Для того чтобы формула численного дифференцирования (36) аппроксимировала 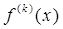с порядком , необходимо и достаточно, чтобы ее коэффициенты 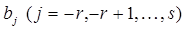являлись решением системы линейных уравнений

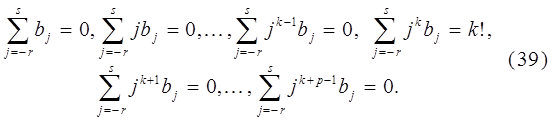
Система (39) содержит уравнений относительно неизвестных .

Из теоремы 6 следует, что для построения искомой формулы численного дифференцирования (36) нужно найти решение системы (39). Выберем 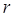и так, чтобы . В этом случае определитель системы (39) есть определитель Вандермонда и отличен от нуля:

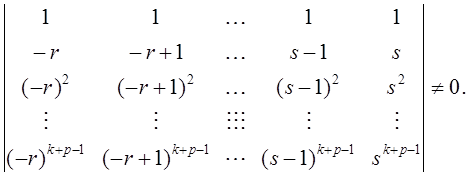
Таким образом, для любых 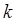и 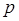можно построить формулу численного дифференцирования, аппроксимирующую 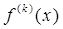с порядком .

2.3. Задание. Для заданных 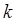и 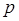методом неопределенных коэффициентовпостроить формулу численного дифференцирования, аппроксимирующую 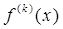с порядком .

Составитель Трофимов Валерий Павлович

Редактор Тихомирова О.А.

Дата добавления: 2014-11-18