
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Квадратурные формулы Гаусса
|
|
|
|
Формула трех восьмых
Формула Симпсона (парабол)
Формула трапеций
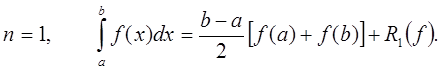
Если  , то
, то 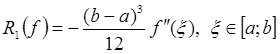 .
.

Если 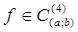 , то
, то 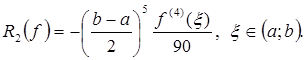
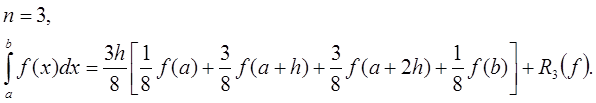
Если 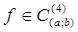 , то
, то 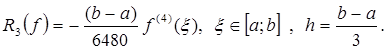
Пусть требуется построить квадратурнуюформулу с 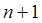 узлами, имеющую максимально возможный алгебраический порядок точности. Нужно определить
узлами, имеющую максимально возможный алгебраический порядок точности. Нужно определить 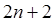 параметра квадратурной формулы: узлы
параметра квадратурной формулы: узлы 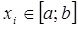 и коэффициенты
и коэффициенты 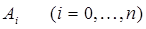 .
.
Ясно, что наивысший алгебраический порядок точности квадратурной формулы с 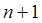 узлами не может быть выше, чем
узлами не может быть выше, чем 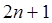 . Действительно, возьмем многочлен
. Действительно, возьмем многочлен 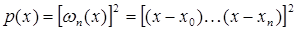 степени
степени 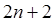 . Тогда
. Тогда 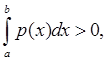 но
но 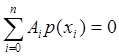 и, следовательно, погрешность квадратурной формулы
и, следовательно, погрешность квадратурной формулы 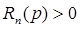 .
.
Теперь мы можем попытаться построить квадратурную формулу с алгебраическим порядком точности 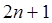 .
.
Теорема 3. Для того чтобы квадратурная формула (2) с 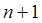 узлами
узлами 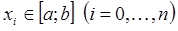 имела алгебраический порядок точности
имела алгебраический порядок точности 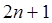 , необходимо и достаточно, чтобы многочлен
, необходимо и достаточно, чтобы многочлен 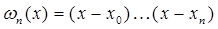 степени
степени 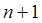 был ортогонален на
был ортогонален на 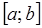 любому многочлену
любому многочлену 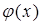 степени меньшей или равной
степени меньшей или равной 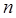
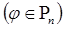 , то есть для любого многочлена
, то есть для любого многочлена 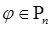
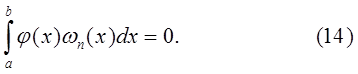
Квадратурная формула с 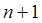 узлами, имеющая алгебраический порядок точности
узлами, имеющая алгебраический порядок точности 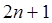 , называется квадратурной формулой Гаусса или квадратурной формулой наивысшего алгебраического порядка точности. Очевидно, что квадратурная формула Гаусса является интерполяционной.
, называется квадратурной формулой Гаусса или квадратурной формулой наивысшего алгебраического порядка точности. Очевидно, что квадратурная формула Гаусса является интерполяционной.
Для любого 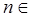 N многочлен степени
N многочлен степени 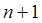 , удовлетворяющий условию ортогональности (14), имеющий вещественные и различные корни
, удовлетворяющий условию ортогональности (14), имеющий вещественные и различные корни 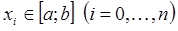 , существует и единственен. Поэтому квадратурная формула Гаусса может быть построена.
, существует и единственен. Поэтому квадратурная формула Гаусса может быть построена.
Для коэффициентов 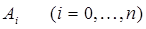 квадратурной формулы Гаусса верно следующее равенство
квадратурной формулы Гаусса верно следующее равенство
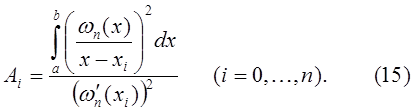
Следовательно, все 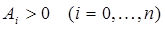 и
и 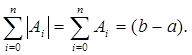 Отсюда и из теоремы 2 вытекает сходимость квадратурного процесса, порожденного квадратурной формулой Гаусса.
Отсюда и из теоремы 2 вытекает сходимость квадратурного процесса, порожденного квадратурной формулой Гаусса.
Квадратурная формула Гаусса дает высокую точность в том случае, когда подинтегральная функция 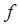 в окрестности отрезка интегрирования обладает высоким порядком гладкости.
в окрестности отрезка интегрирования обладает высоким порядком гладкости.
Погрешность квадратурной формулы Гаусса для 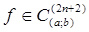 имеет вид
имеет вид
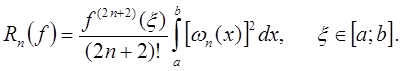
Исторически первым примером квадратурной формулы, имеющей наивысший алгебраический порядок точности, была формула Гаусса для отрезка 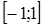 . Для построения квадратурной формулы использовалась система ортогональных многочленов Лежандра.
. Для построения квадратурной формулы использовалась система ортогональных многочленов Лежандра.
Многочлены вида
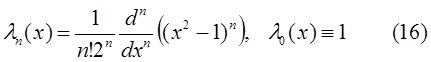
называются многочленами Лежандра. Из (16) следует, что 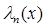 является многочленом степени
является многочленом степени 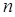 .
.
Многочлены Лежандра обладают следующими свойствами:
1. Многочлен 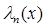 ортогонален на отрезке
ортогонален на отрезке 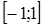 любому многочлену
любому многочлену 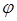 степени меньше
степени меньше 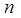 :
: 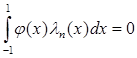 для любого
для любого 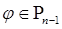 .
.
2. Все корни многочлена 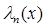 вещественные, различные и расположены на интервале
вещественные, различные и расположены на интервале 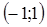 .
.
3. Многочлены 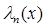 образуют ортогональную систему на
образуют ортогональную систему на 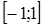 :
: 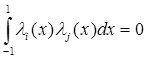 при
при 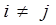 и
и 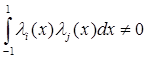 при
при 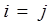 .
.
4. Имеет место рекуррентная формула:
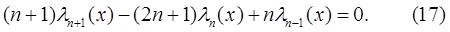
Формула (17) позволяет, используя равенства 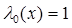 и
и 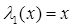 , найти многочлен Лежандра любой степени.
, найти многочлен Лежандра любой степени.
Если известны корни 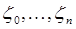 многочлена Лежандра
многочлена Лежандра 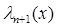 , то, используя (15), получаем квадратурную формулу Гаусса
, то, используя (15), получаем квадратурную формулу Гаусса
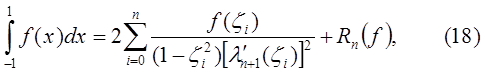
где
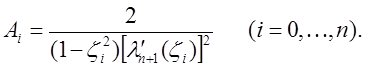
Таблицы узлов и коэффициентов формулы (18) приведены в [3]. Отметим, что корни 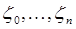 многочленов Лежандра
многочленов Лежандра 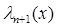 и коэффициенты
и коэффициенты 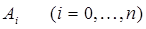 квадратурной формулы (18) обладают симметрией на
квадратурной формулы (18) обладают симметрией на 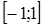 относительно точки
относительно точки 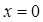 .
.
Пересчет узлов и коэффициентов квадратурной формулы на произвольный отрезок 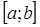 осуществляется с помощью замены переменной
осуществляется с помощью замены переменной 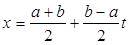 :
:
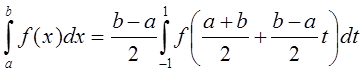
Таким образом, из (18) получаем квадратурную формулу Гаусса для произвольного отрезка 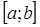
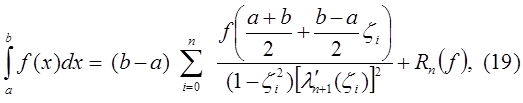
где 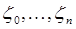 корни многочлена Лежандра
корни многочлена Лежандра 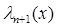 .
.
|
|
|
|
|
Дата добавления: 2014-11-18; Просмотров: 3566; Нарушение авторских прав?; Мы поможем в написании вашей работы!