
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свободные колебания в RLC контуре
|
|
|
|
Указания по технике безопасности
Осторожно обращайтесь с оборотным маятником. Не допускайте падений и ударов маятника, это может нарушить его регулировку.
Лабораторная работа №3
Цель работы:
* Знакомство с моделью свободных колебаний в последовательном RLC-контуре.
* Экспериментальное исследование закономерностей свободных незатухающих и затухающих колебаний.
* Экспериментальное определение характеристик затухания в RLC-контуре.
Основные понятия:
В электрических цепях, так же как и в механических системах, таких как груз на пружине или маятник, могут возникать свободные колебания. Простейшей электрической системой, способной совершать свободные колебания, является последовательный RLC-контур

Закон Ома для замкнутой RLC-цепи, не содержащей внешнего источника тока, записывается в виде
 (1)
(1)
где 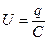 – напряжение на конденсаторе, q – заряд конденсатора,
– напряжение на конденсаторе, q – заряд конденсатора,  – ток в цепи. В правой части этого соотношения стоит ЭДС самоиндукции катушки. Уравнение, описывающее свободные колебания в RLC-контуре, может быть приведено к следующему виду, если в качестве переменной величины выбрать заряд конденсатора q(t):
– ток в цепи. В правой части этого соотношения стоит ЭДС самоиндукции катушки. Уравнение, описывающее свободные колебания в RLC-контуре, может быть приведено к следующему виду, если в качестве переменной величины выбрать заряд конденсатора q(t):
 (2)
(2)
Рассмотрим сначала случай, когда в контуре нет потерь электромагнитной энергии (R = 0). Тогда
 (3)
(3)
Здесь принято обозначение:  Уравнение (3) описывает свободные колебания в LC-контуре в отсутствие затухания.
Уравнение (3) описывает свободные колебания в LC-контуре в отсутствие затухания.
В отсутствие затухания свободные колебания в электрическом контуре являются гармоническими, то есть происходят по закону
q(t) = q0cos(ωt + φ0) (4)
Параметры L и C колебательного контура определяют только собственную частоту свободных колебаний
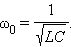 (5)
(5)
Амплитуда q0 и начальная фаза φ0 определяются начальными условиями, то есть тем способом, с помощью которого система была выведена из состояния равновесия.
При свободных колебаниях происходит периодическое превращение электрической энергии Wэ, запасенной в конденсаторе, в магнитную энергию Wм катушки и наоборот. Если в колебательном контуре нет потерь энергии, то полная электромагнитная энергия системы остается неизменной:
 (6)
(6)
Все реальные контура содержат электрическое сопротивление R. Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. За каждый период колебаний часть электромагнитной энергии, запасенной в контуре, превращается в джоулево тепло, и колебания становятся затухающими (рисунок 2).

Рисунок 2 Затухающие колебания
Затухающие колебания в электрическом контуре аналогичны затухающим колебаниям груза на пружине при наличии вязкого трения, когда сила трения изменяется прямо пропорционально скорости тела: Fтр = – dυ. Коэффициент d в этой формуле аналогичен сопротивлению R в электрическом контуре. Уравнение свободных колебаний в контуре при наличии затухания имеет вид
 (7)
(7)
Физическая величина δ = R / 2L называется коэффициентом затухания. Решением этого дифференциального уравнения является функция
 , (8),
, (8),
где  -амплитуда затухающих колебаний,
-амплитуда затухающих колебаний,  - начальная амплитуда.
- начальная амплитуда.
Скорость затухания зависит от электрического сопротивления R контура. Интервал времени  , (9)
, (9)
в течение которого амплитуда колебаний уменьшается в e ≈ 2,7 раза, называется временем затухания.
Для характеристики степени затухания в контуре, кроме величины δ, вводят понятие логарифмического декремента затухания q. Он равен натуральному логарифму отношения двух последующих амплитуд (отстоящих во времени на один период)
 , (10)
, (10)
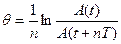 , (11)
, (11)
 . (12)
. (12)
Добротность Q колебательной системы вычисляется:

Добротности Q любой колебательной системы, способной совершать свободные колебания, может быть дано энергетическое определение:

Для RLC-контура добротность Q выражается формулой

Добротность электрических контуров, применяемых в радиотехнике, обычно порядка нескольких десятков и даже сотен.
Следует отметить, что собственная частота ω свободных колебаний в контуре с не очень высокой добротностью несколько меньше собственной частоты ω0 идеального контура с теми же значениями L и C. Но при Q ≥ (5 – 10) этим различием можно пренебречь.
Расчетные формулы:
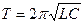 - период незатухающих колебаний,
- период незатухающих колебаний,
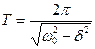 - период затухающих колебаний,
- период затухающих колебаний,
 - время затухания,
- время затухания,
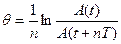 - логарифмический декремент затухания,
- логарифмический декремент затухания,
добротность RLC-контура:  ,
,
 ,
,

Перейдите от окна теории к окну модели, щелкнув по изображению «Модель. Свободные колебания в RLC-контуре». Внимательно рассмотрите рисунок, найдите все регуляторы и другие основные элементы.

Нажмите кнопку «Старт».Пронаблюдайте картину затухающих колебаний в RLC-контуре. Установите значение R=0. Пронаблюдайте картину незатухающих колебаний. Получите у преподавателя допуск для выполнения измерений.
Порядок измерений и обработка результатов:
ЭКСПЕРИМЕНТ 1. Определение периода затухающих и незатухающих колебаний.
- Установите значение L и C, соответствующее вашей бригаде. Установите значение R=0.
- Выберите график Q(t) (для бригад 1-4), выберите график I(t) (для бригад 5-8), нажмите кнопку «Старт». Нажимая кнопку «Стоп», засеките время n полных колебаний, где n=1 - 7.
- Рассчитайте период колебаний
 для каждого значения n. Вычислите среднее значение периода.
для каждого значения n. Вычислите среднее значение периода. - Рассчитайте период колебаний, исходя из параметров RLC-контура
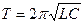 .
. - Сравните значения периода, полученные в пп. 3 и 4 со значением периода, выведенным на экране.
- Повторите измерения и расчеты пп. 2-5 для незатухающих колебаний, установив значение R, соответствующее вашей бригаде.
ТАБЛИЦА 1. Параметры RLC-контура (не перерисовывать)
| Бригада | ||||||||
| L [мГн] | ||||||||
| C [мкФ] | ||||||||
| R[Ом] |
ТАБЛИЦА 2. Результаты измерений при L= ____ мГн, C = ____ мкФ, R=0 Ом.
| n | ti, с |  , с , с
| ||
| T ср =____с |
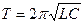 = ____ с, T изм= ____ с
= ____ с, T изм= ____ с
ТАБЛИЦА 3. Результаты измерений при L= ____ мГн, C = ____ мкФ, R=____ Ом.
| n | ti, с |  , с , с
| ||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 | ||||
| T ср =____с |
t = ____ с, 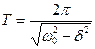 = ____ с, T изм= ____ с
= ____ с, T изм= ____ с
ЭКСПЕРИМЕНТ 2 Определение логарифмического декремента затухания.
- Выберите график q(t).
- Запишите значение
 . Измерьте с помощью линейки (или нажимая кнопку «Стоп») амплитуду колебаний через n=3 полных колебаний
. Измерьте с помощью линейки (или нажимая кнопку «Стоп») амплитуду колебаний через n=3 полных колебаний  .
. - Рассчитайте логарифмический декремент затухания
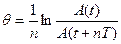 .
. - Повторите измерения пп. 2-3 еще 3 раза.
- Рассчитайте среднее значение логарифмического декремента затухания.
- Рассчитайте логарифмический декремент затухания по формуле
 .
. - Сравните полученные результаты.
ТАБЛИЦА 4. Логарифмический декремент затухания
 = = 
| 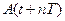
| 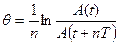
| 
|
ЭКСПЕРИМЕНТ 3 Определение добротности контура.
- Определите начальную энергию RLC-контура W0, нажмите кнопку «Старт». Нажимая кнопку «Стоп», определите энергию через одно полное колебание W1.
- Рассчитайте потерю энергии за один период
 .
. - Рассчитайте добротность
 .
. - Повторите измерения полной энергии через период W2, W3, W4, W5, каждый раз вычисляя потерю энергии за период
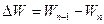 и добротность
и добротность 
- Рассчитайте среднее значение Q.
- Сравните полученный результат с результатом расчетной формулы
 .
. - Вычислите добротность контура по формуле

ТАБЛИЦА 5. Добротность контура
| № | Wn-1 | Wn | 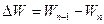
| 
| 
| 
|
| Qср |
Лабораторная работа №4
|
|
|
|
|
Дата добавления: 2014-11-18; Просмотров: 1470; Нарушение авторских прав?; Мы поможем в написании вашей работы!