
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вынужденные колебания
|
|
|
|
Цель работы:
Знакомство с компьютерной моделью вынужденных механических колебаний.
Экспериментальное исследование амплитудно-частотной характеристики пружинного маятника.
Основные понятия:
Колебания, совершающиеся под воздействием внешней периодической силы, называются вынужденными.
Внешняя сила совершает положительную работу и обеспечивает приток энергии к колебательной системе. Она не дает колебаниям затухать, несмотря на действие сил трения.
Периодическая внешняя сила может изменяться во времени по различным законам. Особый интерес представляет случай, когда внешняя сила, изменяющаяся по гармоническому закону с частотой ω, воздействует на колебательную систему, способную совершать собственные колебания на некоторой частоте ω0.
Если свободные колебания происходят на частоте ω0, которая определяется параметрами системы, то установившиеся вынужденные колебания всегда происходят на частоте ω внешней силы.
После начала воздействия внешней силы на колебательную систему необходимо некоторое время Δt для установления вынужденных колебаний. Время установления по порядку величины равно времени затухания τ свободных колебаний в колебательной системе.
В начальный момент в колебательной системе возбуждаются оба процесса – вынужденные колебания на частоте ω и свободные колебания на собственной частоте ω0. Но свободные колебания затухают из-за неизбежного наличия сил трения. Поэтому через некоторое время в колебательной системе остаются только стационарные колебания на частоте ω внешней вынуждающей силы.
Рассмотрим в качестве примера вынужденные колебания тела на пружине (рис. 2.5.1). Внешняя сила  приложена к свободному концу пружины. Она заставляет свободный (левый на рис. 2.5.1) конец пружины перемещаться по закону
приложена к свободному концу пружины. Она заставляет свободный (левый на рис. 2.5.1) конец пружины перемещаться по закону
y = ym cos ωt,
где ym – амплитуда колебаний, ω – круговая частота.
Такой закон перемещения можно обеспечить с помощью шатунного механизма, не показанного на рисунке 1.
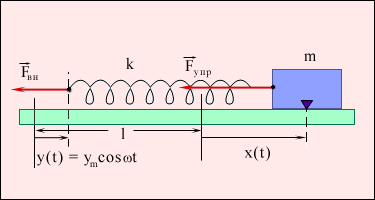
Рисунок 1. Вынужденные колебания груза на пружине.
Свободный конец пружины перемещается по закону y = ym cos ωt. l – длина недеформированной пружины, k – жесткость пружины
Если левый конец пружины смещен на расстояние y, а правый – на расстояние x от их первоначального положения, когда пружина была недеформирована, то удлинение пружины Δl равно:
Δl = x – y = x – ym cos ωt.
Второй закон Ньютона для тела массой m:
ma = –k(x – y) = –kx + kym cos ωt.
В этом уравнении сила, действующая на тело, представлена в виде двух слагаемых. Первое слагаемое в правой части – это упругая сила, стремящаяся возвратить тело в положение равновесия (x = 0). Второе слагаемое – внешнее периодическое воздействие на тело. Это слагаемое и называют вынуждающей силой.
Уравнению, выражающему второй закон Ньютона для тела на пружине при наличии внешнего периодического воздействия, можно придать строгую математическую форму, если учесть связь между ускорением тела и его координатой: 
Тогда уравнение вынужденных колебаний запишется в виде

где  – собственная круговая частота свободных колебаний, ω – циклическая частота вынуждающей силы. В случае вынужденных колебаний груза на пружине (рис. 2.5.1) величина
– собственная круговая частота свободных колебаний, ω – циклическая частота вынуждающей силы. В случае вынужденных колебаний груза на пружине (рис. 2.5.1) величина  определяется выражением:
определяется выражением:
 .
.
Это уравнение не учитывает действия сил трения.
С учетом сил трения уравнение вынужденных колебаний имеет вид:
 ,
,
где 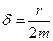 - коэффициент затухания.
- коэффициент затухания.
Решение этого дифференциального уравнения состоит из двух частей: общего решения и частного решения:
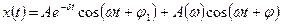 ,
,
где первое слагаемое отвечает собственным затухающим колебаниям, а второе – вынужденным.
Установившиеся вынужденные колебания груза на пружине происходят на частоте внешнего воздействия по закону
x(t) = А(w)cos (ωt + j).
Можно показать, что xm и j зависят от ω следующим образом:
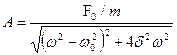 ,
,
 .
.
Амплитуда вынужденных колебаний при 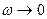

На очень низких частотах, когда ω << ω0, движение тела массой m, прикрепленного к правому концу пружины, повторяет движение левого конца пружины. При этом x(t) = y(t), и пружина остается практически недеформированной. Внешняя сила  , приложенная к левому концу пружины, работы не совершает, т. к. модуль этой силы при ω << ω0 стремится к нулю.
, приложенная к левому концу пружины, работы не совершает, т. к. модуль этой силы при ω << ω0 стремится к нулю.
Если частота ω внешней силы приближается к собственной частоте ω0, возникает резкое возрастание амплитуды вынужденных колебаний. Это явление называется резонансом. Зависимость амплитуды xm вынужденных колебаний от частоты ω вынуждающей силы называется резонансной характеристикой или резонансной кривой (рисунок 2).
При резонансе амплитуда xm колебания груза может во много раз превосходить амплитуду ym колебаний свободного (левого) конца пружины, вызванного внешним воздействием. В отсутствие трения амплитуда вынужденных колебаний при резонансе должна неограниченно возрастать. В реальных условиях амплитуда установившихся вынужденных колебаний определяется условием: работа внешней силы в течение периода колебаний должна равняться потерям механической энергии за то же время из-за трения. Чем меньше трение (т. е. чем выше добротность Q колебательной системы), тем больше амплитуда вынужденных колебаний при резонансе.
У колебательных систем с не очень высокой добротностью (< 10) резонансная частота несколько смещается в сторону низких частот. Это хорошо заметно на рисунке 2.

Рисунок 2. Амплитудно-частотная характеристика
Резонансные кривые при различных уровнях затухания: 1 – колебательная система без трения; при резонансе амплитуда xm вынужденных колебаний неограниченно возрастает; 2, 3, 4 – реальные резонансные кривые для колебательных систем с различной добротностью: Q2 > Q3 > Q4. На низких частотах (ω << ω0) xm ≈ ym. На высоких частотах (ω >> ω0) xm → 0.
Перейдите от окна теории к окну модели, щелкнув по изображению «Модель. Вынужденные колебания». Внимательно рассмотрите рисунок, найдите все регуляторы и другие основные элементы.
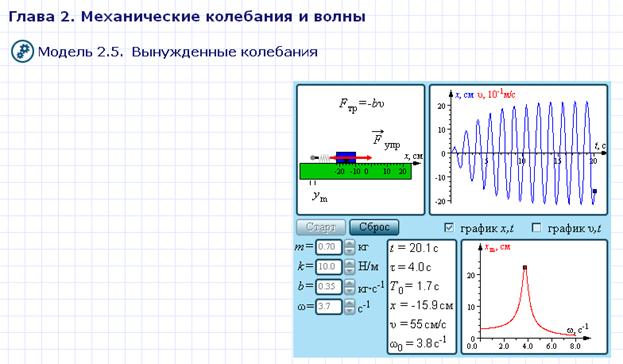
Обратите внимание, что в данной работе коэффициент вязкого трения r обозначен как b. Установите флажок к графику x,t и v,t. Нажмите кнопку «Старт». Пронаблюдайте картину вынужденных колебаний пружинного маятника, изменяя параметры колебательной системы. Обратите внимание на то, что установившиеся вынужденные колебания всегда происходят на частоте вынуждающей силы. Получите у преподавателя допуск для выполнения измерений.
Порядок измерений и обработка результатов:
ЭКСПЕРИМЕНТ 1. Определение резонансной частоты колебательной системы.
- Установите значения m, r1 и k, соответствующие вашей бригаде
- Выберите график x,t (для бригад 1-4), выберите график v,t (для бригад 5-8).
- Установите значение частоты вынуждающей силы w=3.0 с-1. Измерьте с помощью линейки (или нажимая кнопку «Стоп») амплитуду установившихся колебаний x max.
- Увеличивая значение частоты на 0.5 с-1, наблюдайте вынужденные колебания. Повторите измерение амплитуды. При частоте, близкой к частоте резонанса, значение частоты изменяйте через 0.1 с-1. Результаты заносите в таблицу 2.
- Установите значение частоты вынуждающей силы w=w0. Пронаблюдайте явление резонанса. Измерьте амплитуду.
- Постройте амплитудно-частотную характеристику A (w).
- Повторите измерения пп. 3-5 для двух других значений коэффициента вязкого трения r, увеличивая его значение на 0.2 кг×с-1. Постройте амплитудно-частотную характеристику A (w) для r2 и r3 на том же графике.
ТАБЛИЦА 1. Параметры колебательной системы (не перерисовывать)
| Бригада | ||||||||
| m [кг] | ||||||||
| k [Н/м] | ||||||||
| r=b[кг×с-1] |
ТАБЛИЦА 2. Результаты измерений при m= ____ кг, k = ____ Н/м.
| r1= ____кг×с-1. | r2= ____кг×с-1. | r3= ____кг×с-1. | ||||
| № | w, с-1 | A., см | w, с-1 | A., см | w, с-1 | A., см |
| w0= | w0= | w0= |
Приложение 1 Бланки Лабораторных работ
Лабораторная работа № 1
Изучение собственных колебаний механических систем
| Фамилия И.О. | |
| Группа | |
| № бригады |
ТАБЛИЦА 1. Характеристики приборов измерения
| Прибор | Предел измерений | Цена деления | Погрешность прибора |
| Линейка | |||
| Секундомер |
ТАБЛИЦА 2. Статический метод определения собственной частоты незатухающих колебаний пружинного маятника
| l0 | l | xст =l - l0 | 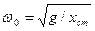
| e(w0)=Dl/xст | Dw0=w0*e(w0) |
| w0 ± Dw0 |
ТАБЛИЦА 3. Динамический метод определения собственной частоты затухающих колебаний пружинного маятника
| № | n=10; tn,c | Dtni,c | Dtni2,c | Расчетные формулы |
| 1. | N=5;  ; ;  a=0,9; ta(N)=; Dtсл=ta(N)S=;
Dt=Dtсл+Dtпр=; e(w1)=Dt/(t*n)
Dw1=w1*e(w1)
a=0,9; ta(N)=; Dtсл=ta(N)S=;
Dt=Dtсл+Dtпр=; e(w1)=Dt/(t*n)
Dw1=w1*e(w1)
| |||
| 2. | ||||
| 3. | ||||
| 4. | ||||
| 5. | ||||
| T | SDtni2 | |||
 ; w1 ± Dw1; ; w1 ± Dw1;
|
ТАБЛИЦА 4. Определение логарифмического декремента затухания колебаний пружинного маятника динамическим методом
| № | A0 | An | n | 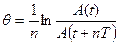
| qср |
| 1. | |||||
| 2. | |||||
| 3. | |||||
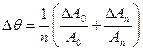 =; q ± Dq =; q ± Dq
|
Лабораторная работа № 2.
Измерение ускорения свободного падения с помощью математического и физического маятников
| Фамилия И.О. | |
| Группа | |
| № бригады |
таблица 1 Характеристики приборов измерения:
| Прибор | Предел измерений | Цена деления | Погрешность прибора |
| Линейка | |||
| Электронный секундомер |
таблица 2 Исходные данные для проведения опытов:
| длина нити математического маятника l, м | расстояние между остриями опор оборотного маятника l0, м |
таблица 3 Измерение периода колебаний математического маятника
| l, м | T,с | ∆T i ,с | ∆T i 2 ,с | g, м/с2 |

| ||||
| Tср,с | Σ∆T i 2 |
 DTсл=ta(N)S= DT=DTсл+DTпр=
DTсл=ta(N)S= DT=DTсл+DTпр=
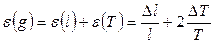

таблица 4 Измерение периода колебаний оборотного маятника
| l0, м | T,с | ∆T i ,с | ∆T i 2 ,с | g, м/с2 |

| ||||
| Tср,с | Σ∆T i 2 |
 DTсл=ta(N)S= DT=DTсл+DTпр=
DTсл=ta(N)S= DT=DTсл+DTпр=


Лабораторная работа № 3.
Свободные колебания в RLC-контуре
| Фамилия И.О. | |
| Группа | |
| № бригады |
ТАБЛИЦА 1. Параметры RLC-контура (не перерисовывать)
| Бригада | ||||||||
| L [мГн] | 10,0 | 9,5 | 9,0 | 8,5 | 8,0 | 7,5 | 7,0 | 6,5 |
| C [мкФ] | 5,5 | 5,0 | 4,5 | 4,0 | 3,5 | 3,0 | 2,5 | 2,0 |
| R[Ом] | 4,0 | 4,2 | 4,4 | 4,6 | 4,8 | 5,0 | 5,2 | 5,4 |
ТАБЛИЦА 2. Результаты измерений при L= ____ мГн, C = ____ мкФ, R=0 Ом.
| n | ti, с |  , с , с
| ||
| T ср =____с |
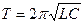 = ____ с, T изм= ____ с
= ____ с, T изм= ____ с
ТАБЛИЦА 3. Результаты измерений при L= ____ мГн, C = ____ мкФ, R=____ Ом.
| n | ti, с |  , с , с
| ||
| T ср =____с |
t = ____ с, 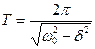 = ____ с, T изм= ____ с
= ____ с, T изм= ____ с
ЭКСПЕРИМЕНТ 2 Определение логарифмического декремента затухания.
ТАБЛИЦА 3. Логарифмический декремент затухания
 = = 
| 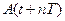
| 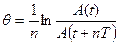
| 
|
ЭКСПЕРИМЕНТ 3 Определение добротности контура.
ТАБЛИЦА 4. Добротность контура
| № | Wn-1 | Wn | 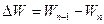
| 
| 
| 
|
| Qср |
Лабораторная работа № 4.
Вынужденные колебания
| Фамилия И.О. | |
| Группа | |
| № бригады |
ТАБЛИЦА 1. Параметры колебательной системы (не перерисовывать)
| Бригада | ||||||||
| m [кг] | 0,55 | 0,60 | 0,65 | 0,70 | 0,75 | 0,80 | 0,85 | 0,90 |
| k [Н/м] | 6,0 | 6,5 | 7,0 | 7,5 | 8,0 | 8,5 | 9,0 | 9,5 |
| r1=b[кг×с-1] | 0,35 | 0,40 | 0,35 | 0,40 | 0,35 | 0,40 | 0,35 | 0,40 |
ТАБЛИЦА 2. Результаты измерений при m= ____ кг, k = ____ Н/м.
| r1= ____кг×с-1. | r2= ____кг×с-1. | r3= ____кг×с-1. | ||||
| № | w, с-1 | A., см | w, с-1 | A., см | w, с-1 | A., см |
| w0= | w0= | w0= |
Приложение 2 Таблица коэффициентов Стьюдента
| Число измерений | Коэффициент надежности | |||||||
| n | 0,8 | 0,9 | 0,95 | 0,975 | 0,99 | 0,995 | 0,999 | 0,9995 |
| 1,38 | 3,08 | 6,31 | 12,71 | 31,82 | 63,66 | 318,31 | 636,62 | |
| 1,06 | 1,89 | 2,92 | 4,30 | 6,97 | 9,93 | 22,33 | 31,60 | |
| 0,98 | 1,64 | 2,35 | 3,18 | 4,54 | 5,84 | 10,21 | 12,94 | |
| 0,94 | 1,53 | 2,13 | 2,78 | 3,75 | 4,60 | 7,17 | 8,61 | |
| 0,92 | 1,48 | 2,02 | 2,57 | 3,37 | 4,03 | 5,89 | 6,86 | |
| 0,91 | 1,44 | 1,94 | 2,45 | 3,14 | 3,71 | 5,21 | 5,96 | |
| 0,90 | 1,42 | 1,90 | 2,37 | 3,00 | 3,50 | 4,78 | 5,41 | |
| 0,89 | 1,40 | 1,86 | 2,31 | 2,90 | 3,36 | 4,50 | 5,04 | |
| 0,88 | 1,38 | 1,83 | 2,26 | 2,82 | 3,25 | 4,30 | 4,78 | |
| 0,88 | 1,37 | 1,81 | 2,23 | 2,76 | 3,17 | 4,14 | 4,59 | |
| 0,88 | 1,36 | 1,80 | 2,20 | 2,72 | 3,11 | 4,02 | 4,44 | |
| 0,87 | 1,36 | 1,78 | 2,18 | 2,68 | 3,06 | 3,93 | 4,32 | |
| 0,87 | 1,35 | 1,77 | 2,16 | 2,65 | 3,01 | 3,85 | 4,22 | |
| 0,87 | 1,34 | 1,76 | 2,15 | 2,62 | 2,98 | 3,79 | 4,14 | |
| 0,87 | 1,34 | 1,75 | 2,13 | 2,60 | 2,95 | 3,73 | 4,07 | |
| 0,86 | 1,34 | 1,75 | 2,12 | 2,58 | 2,92 | 3,69 | 4,02 | |
| 0,86 | 1,33 | 1,74 | 2,11 | 2,57 | 2,90 | 3,65 | 3,97 | |
| 0,86 | 1,33 | 1,73 | 2,10 | 2,55 | 2,88 | 3,61 | 3,92 | |
| 0,86 | 1,33 | 1,73 | 2,09 | 2,54 | 2,86 | 3,58 | 3,88 | |
| 0,86 | 1,33 | 1,73 | 2,09 | 2,53 | 2,85 | 3,55 | 3,85 | |
| 0,86 | 1,32 | 1,72 | 2,08 | 2,52 | 2,83 | 3,53 | 3,82 | |
| 0,86 | 1,32 | 1,72 | 2,07 | 2,51 | 2,82 | 3,50 | 3.79 | |
| 0,86 | 1,32 | 1,71 | 2,07 | 2,50 | 2,81 | 3,48 | 3,77 | |
| 0,86 | 1,32 | 1,71 | 2,06 | 2,49 | 2,80 | 3,47 | 3,75 | |
| 0,85 | 1,31 | 1,70 | 2,04 | 2,46 | 2,75 | 3,39 | 3,65 | |
| 0,85 | 1,30 | 1,68 | 2,02 | 2,42 | 2,70 | 3,31 | 3,55 | |
| 0,85 | 1,30 | 1,67 | 2,00 | 2,39 | 2,66 | 3,23 | 3,46 | |
| 0,84 | 1,29 | 1,66 | 1,98 | 2,36 | 2,62 | 3,16 | 3,37 | |
| ∞ | 0,84 | 1,28 | 1,64 | 1,96 | 2,33 | 2,58 | 3,09 | 3,29 |
Приложение 3 Контрольные вопросы
|
|
|
|
|
Дата добавления: 2014-11-18; Просмотров: 864; Нарушение авторских прав?; Мы поможем в написании вашей работы!