Элементы статистической обработки данных 1 страница

Москва

Часть первая

МАТЕМАТИКА

Под редакцией Д. А. Ловцова

УДК 51

ББК 22.1

М 21

Авторы

В.Т. Королев

профессор, кандидат технических наук,

Д.А. Ловцов

профессор, доктор технических наук,

Радионов В.В.

доцент, кандидат технических наук,

Редактор:

Д.А. Ловцов

профессор, доктор технических наук,

Математика / Под ред. Д.А. Ловцова. –М.: РАП, 2013.

Содержание учебного пособия (часть первая) отвечает требованиям ФГОС высшего профессионального образования по специальности 031003.65 – «Судебная экспертиза», а также по направлениям подготовки 080100.62 – «Экономика», 080200.62 – «Менеджмент».

Изложены основания математики, начала математического анализа с элементами алгоритмов решения вычислительных задач, введение в теорию вероятностей, оснвы защиты информации.

Пособие адресовано студентам специалитета и баклаврита вузов. Им могут пользоваться и преподаватели, ведущие занятия по этой и родственным дисциплинам, а также эксперты, которые самостоятельно изучают элементы высшей математики.

© В.Т. Королев, Д.А. Ловцов, В.В. Радионов, 2013

© Российская академия правосудия, 2013

СОДЕРЖАНИЕ

ПРЕДИСЛОВИЕ. 5

ВВЕДЕНИЕ. 9

РАЗДЕЛ I ОСНОВАНИЯ МАТЕМАТИКИ. 12

Глава 1. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ. 12

1.1. Понятие множества. 12

1.2. Операции над множествами. 14

1.3. Аксиомы и теоремы алгебры множеств. 18

Вопросы и задачи для самоконтроля. 20

Глава 2. ЧИСЛА. 21

2.1. Системы счисления. 21

2.2. Классы чисел. 26

2.4. Алгоритмы решения вычислительных задач. 35

Вопросы и задачи для самоконтроля. 39

Глава 3. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ. 40

3.1. Понятие высказывания. 40

3.2. Операции над высказываниями. 42

2.3. Аксиомы и теоремы алгебры логики. 51

Вопросы и задачи для самоконтроля. 57

РАЗДЕЛ II ОСНОВЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА. 59

Глава 4. ФУНКЦИИ. 59

4.1. Понятие функции. 59

4.2. Аппроксимация функций. 65

4.3. Предел функции. 69

Вопросы и задачи для самоконтроля. 77

Глава 5. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ. 78

5.1. Производная функции. 78

5.2. Свойства дифференцируемых функций. 82

5.3. Дифференциал функции. 85

Вопросы и задачи для самоконтроля. 87

Глава 6. ОСНОВЫ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ. 88

6.1. Определенный интеграл. 88

6.2. Машинные алгоритмы вычисления определенных интегралов 99

Вопросы и задачи для самоконтроля. 106

РАЗДЕЛ III ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ. 108

Глава 7. ПОНЯТИЕ ВЕРОЯТНОСТИ. 108

7.1. Элементы комбинаторики. 108

7.2. Случайные события. 115

7.3. Классическое определение вероятности. 122

7.4. Теорема умножения вероятностей. 125

7.5. Основные формулы теории вероятностей. 129

Вопросы и задачи для самоконтроля. 135

Глава 8. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ.. 137

8.1. Понятие случайной величины. 137

8.2. Законы распределения случайных величин. 138

8.3. Числовые характеристики случайных величин. 145

8.4. Канонические распределения случайных величин. 152

8.5. Энтропия и информация. 158

Вопросы и задачи для самоконтроля. 170

РАЗДЕЛ IV. ОСНОВНЫЕ СПОСОБЫ И МЕТОДЫ ЗАЩИТЫ ИНФОРМАЦИИ 173

Глава 9. ОСНОВЫ КРИПТОГРАФИЧЕСКОЙ ЗАЩИТЫ ИНФОРМАЦИИ 173

9.1. Принципы и основные понятия
криптографической защиты информации. 173

9.2. Основные понятия и определения. 179

Вопросы и задачи для самоконтроля. 182

Глава 10. МЕТОДЫ КРИПТОГРАФИЧЕСКОЙ ЗАЩИТЫ ИНФОРМАЦИИ 182

10.1. Методы перестановки. 183

10.2. Метод гаммирования. 188

Вопросы и задачи для самоконтроля. 194

ОТВЕТЫ К ЗАДАЧАМ.. 195

ПРИЛОЖЕНИЕ ТЕСТЫ.. 209

ЛИТЕРАТУРА. 239

СВЕДЕНИЯ ОБ АВТОРАХ. 247

ПРЕДИСЛОВИЕ

Зачем юристу, судебному эксперту математика? Ведь юриспруденция считается сугубо гуманитарной областью, и многие из наших читателей пошли учиться в юридическое учебное заведение для того, чтобы не мучиться с математикой. Они считают, что юристу в его будущей работе математика не понадобится, и, стало быть, незачем тратить на нее время. Но это убеждение противоречит практике.

Всякое специальное образование предполагает освоение, наряду с профильными науками, еще и базовых достижений человеческой культуры. Естественные науки (а это – половина (как минимум!) мировой культуры) составляют базис научно-технической революции и опираются на математику. Математика – одна из важнейших составляющих культуры, такая же, как философия, естествознание и др. Любопытно, что существенный вклад в достижения математики внесли юристы. Так, Пьер Ферма (1601-1665) – французский математик, слушал право в Тулузском университете, служил советником кассационной палаты Тулузского парламента. Одна из самых таинственных и фантастических историй в математике связана с великой теоремой Ферма, которая утверждает, что уравнение xⁿ+yⁿ=zⁿ при n>2 не имеет решений в натуральных числах (к примеру, таких, как 3²+4²=5²). Ферма на полях книги древнегреческого математика Диофанта написал, что «открыл этому поистине чудесное доказательство, но эти поля для него слишком узки». С тех пор математики бьются над доказательством этой теоремы, но получили его лишь для двух-трех значений n. Общего доказательства пока нет (видимо, оно ждет своего правоведа). А Готфрид Вильгельм Лейбниц (1646 – 1716) был юристом по образованию, необычайно разносторонним и талантливым ученым, чьи способности с наибольшей силой проявились в математике. Именно юрист Лейбниц впервые ввел в употребление такие математические термины, как абсцисса, ордината, координата, функция, алгоритм и др.

Итак, математика для юристов – это общеобразовательная дисциплина, как право для инженеров или экономика для тех и других.

В юриспруденции, в судебной экспертизе, как и в математике, применяются одинаковые методы построения рассуждений, цель которых – выявить истину. Правовед, как и математик, должен уметь мыслить логически, применять на практике индуктивный (от частного к общему) и дедуктивный (от общего к частному) методы. Математика способствует формированию такого склада ума, при котором критической проверке и логическому обоснованию подвергаются те или иные сведения, утверждения, точки зрения. Математика имеет свой язык, овладев которым, юрист, судебный эксперт приобретает такие важные навыки рационального выражения мысли, как точность, ясность, последовательность, лаконичность, выразительность. Осваивая математику, будущий правовед формирует свое профессиональное мышление. Английский философ и естествоиспытатель Роджер Бэкон говорил: «Кто не знает математики, не может освоить никакой другой науки и даже не в состоянии обнаружить своего невежества».

В то же время и сугубо профессиональная деятельность юриста требует от него математических познаний. Так, сегодня многие правовые акты оперируют с формулами.

Пример. В Законе «О трудовых пенсиях в РФ» (ст. 16, ч. 1) приведена формула:

П=ПК/(Т´К)/КН+Б

(смысл каждого из операндов в статье поясняется).

К сожалению, формула записана небрежно. Правая часть ее по смыслу – многоэтажная дробь. Но здесь она заменена строкой делений, а деление задано символом /. Такая форма записи чревата ошибками в вычислениях. Дело в том, что операции в цепочке сложений без скобок, операции в цепочке умножений без скобок можно выполнять в любом порядке. Бывает, что это распространяют и на цепочку делений. Однако операции в цепочке делений без скобок следует выполнять только в порядке их следования в строке. Запись в традиционной для математики форме

П= 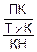+Б

задает единственный порядок выполнения вычислений, и он не зависит от указанной особенности операции деления.

Или такой пример. Суду необходимо определить степень опьянения потерпевшего. В руководстве по судебно-медицинской экспертизе СМЭ приведена следующая шкала о степени опьянения:

ü 1.5 – 2.5 промилле ¾ опьянение средней тяжести,

ü 2.5 – 3.0 промилле ¾ сильное опьянение,

ü 3.0 – 5.0 промилле ¾ тяжелое отравление.

В рамках СМЭ было установлено, что содержание алкоголя в крови потерпевшего составило 2.9 промилле. На первый взгляд результаты экспертизы говорят о том, что потерпевший находился в состоянии сильного опьянения. Однако такой вывод доверия не заслуживает, поскольку в задании на проведение СМЭ погрешность измерений указана не была. На практике, если нет специальных указаний о требуемой точности, подобные измерения выполняются по упрощенной методике с погрешностью в ±20% от измеренного значения. Значит, содержание алкоголя в крови потерпевшего составляло 2.9±0.6 промилле, то есть могло лежать в пределах от 2.3 до 3.5 промилле. В этом случае судья не может сделать никакого вывода о степени опьянения потерпевшего, кроме того, что пьяным он был.

В данном случае были нарушены положения Закона «Об обеспечении единства измерений», в котором говорится, что «единство измерений – состояние измерений, при котором их результаты выражены в узаконенных единицах величин и погрешности измерений не выходят за установленные границы с заданной вероятностью». Для однозначного определения степени опьянения в задании на экспертизу нужно было бы потребовать проведения измерений с погрешностью, существенно меньшей, чем 20%. Конкретное числовое значение требуемой точности измерений можно получить, используя аппарат теории вероятностей.

В практике судебной экспертизы широко проводятся различного рода исследования и эксперименты. При обработке их результатов применяются методы математической статистики. Статистика же опирается на теорию вероятностей. Та, в свою очередь, использует результаты математического анализа, основу которого составляют такие фундаментальные понятия как число, функция, производная, интеграл. А в математическом анализе используется аппарат теории множеств и математической логики. Сказанное и определило структуру первой части учебного пособия. Её содержимое разбито на четыре раздела:

I. Основания математики.

II. Основы математического анализа.

III. Основы теории вероятностей.

IV. Основные способы и методы защиты информации.

Учебный материал изложен на уровне основ, элементов, понятий, в нем нет математических тонкостей, которые не столь важны для будущих юристов. Зато имеется достаточно примеров из области юриспруденции. При разработке таких примеров использовалась «Справочная правовая система «КонсультантПлюс». Поэтому материал вполне доступен студентам как высших, так и средних учебных заведений юридического профиля.

Каждую главу завершает параграф с вопросами и задачами для самоконтроля.

Приложение содержит контрольные домашние задания (КДЗ) – тесты по всем темам. Они используются при проведении текущего контроля за ходом изучения учебного материала.

Наказание и иные меры уголовно-правового характера, применяемые к лицу, совершившему преступление, не могут иметь своей целью причинение физических страданий или унижение человеческого достоинства.

(УК РФ, Ст. 7, ч. 2)

ВВЕДЕНИЕ

Математика – древнейшая из наук. Долгое время она была лишь инструментом для производства вычислений в различных областях человеческой деятельности. Поэтому Ф. Энгельс так определил ее предмет:

математика имеет своим объектом пространственные формы и количественные отношения действительного мира.

Однако по мере своего развития математика все больше и больше превращалась в самодостаточную формализованную науку. С середины XX века она развивается сама по себе, изучая абстрактные объекты, ее результаты (какое-то время, часто достаточно большое) не находят непосредственного применения в практике за пределами самой математики. Это позволило коллективу французских математиков под общим псевдонимом Н. Бурбаки утверждать:

чистая математика представляется скоплением абстрактных форм – математических структур, не имеющих никакого отношения к окружающей действительности.

Абстрактный характер современной математики, с одной стороны, делает ее аппарат универсальным инструментом исследований в любых областях науки, а с другой стороны, существенно затрудняет ее освоение.

В математике изучают структуры трех типов:

§ алгебраические структуры, когда на некотором множестве задается конечное число операций, свойства которых описываются системой аксиом;

§ структуры порядка, которые характеризуются тем, что на рассматриваемом множестве задается отношение следования, когда про любые два элемента из этого множества можно сказать, какой из них предшествует другому;

§ топологические структуры, обладающие тем свойством, что каждому элементу из некоторого множества сопоставляется такое его подмножество, которое называют окрестностью этого элемента.

Например, в арифметике заданы арифметические операции над целыми числами и аксиомы (скажем, такая: от перемены мест слагаемых сумма не изменяется). Значит, целые числа суть алгебраическая структура.

Существуют и составные структуры. Про любые два целых числа можно сказать, какое из них предшествует другому на числовой прямой. А это структура порядка. Поэтому целые числа представляют собою составную структуру.

На протяжении всей истории математики ученые стремились разработать формализованную процедуру построения той или иной математической теории. Первым это сделал древнегреческий математик Евклид в III веке до нашей эры. Он сформулировал систему аксиом, на основе которой построил стройную теорию геометрии. Она оставалась незыблемой почти две тысячи лет. Революционный переворот в этой области совершил Н.И. Лобачевский, который в 1826 г. построил свою геометрию, отличную от евклидовой. Основу ее составила система аксиом Евклида, в которой была изменена только одна аксиома – о параллельных прямых. Теперь она утверждала, что через точку вне прямой проходит более одной прямой, не пересекающей данную. Геометрия Лобачевского оказалась тоже логически стройной и математически строгой теорией, хотя ее положения не подтверждались практикой того времени. В дальнейшем был разработан аксиоматический метод – строго формализованная процедура построения любой дедуктивной теории. Эта процедура сводится к следующей схеме:

1. Выбирается совокупность первичных (фундаментальных) понятий, составляющих предмет теории.

2. Задается набор операций, операндами в которых выступают введенные понятия.

3. Составляется система простых, совместимых и независимых аксиом.

Под аксиомой некоторой теории при ее дедуктивном построении понимается высказывание, принимаемое на веру (без доказательства). Аксиомы отвечают таким требованиям:

P никакую из аксиом нельзя разбить на две или больше частей (аксиомы просты),

P аксиомы не противоречат друг другу, то есть из них нельзя логически вывести два взаимоисключающих утверждения (они совместимы),

P ни одну из аксиом нельзя вывести из совокупности других (аксиомы независимы).

4. Из аксиом путем некоторых рассуждений (или выполнения заданных операций над фундаментальными понятиями) выводятся логические следствия – теоремы, которые и составляют содержание теории.

Приведенная схема дает общее представление о сущности аксиоматического метода. Ниже, следуя этой схеме, мы излагаем раздел «Основания математики» (теорию множеств и математическую логику).

Характерной чертой математики является то, что ее абстрактные методы применимы к объектам произвольной природы, то есть математика остается инструментом познания все более сложных процессов и явлений, в том числе и не только математической природы. Этим обусловлено интенсивное использование математики в самых различных областях науки и практики, включая и сугубо гуманитарные.

Математика для специалиста в той или иной области является орудием, инструментом в его профессиональной деятельности. Поэтому он должен изучать математику для того, чтобы выбрать ту из ее теорий, которая ему кажется подходящей. Далее абстрактным понятиям этой теории придается содержательный смысл из сферы его профессиональной деятельности. В результате, абстрактная теория преобразуется в математическую модель, которая и становится инструментом в руках профессионала.

Если все преступления, совершенные по совокупности, являются преступлениями небольшой и средней тяжести, то окончательное наказание назначается путем поглощения менее строгого наказания более строгим либо путем частичного или полного сложения назначенных наказаний.

(УК РФ, Ст. 69, ч. 2)

РАЗДЕЛ I
ОСНОВАНИЯ МАТЕМАТИКИ

Глава 1. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ

1.1. Понятие множества

Множество – одно из первичных, фундаментальных понятий математики. Однако строгого определения этого понятия в рамках самой теории множеств не существует. Его можно лишь пояснить, приведя примеры множеств. Скажем, множество студентов первого курса академии, множество законодательных актов по правам человека, множество пятен на Солнце и т.д.

Объекты, составляющие множество, называют элементами. Когда это удобно, элементы множества называют точками (например, элементы множества рациональных чисел – точки на числовой прямой). В теории множеств, как и в любой математической теории, используют свою систему обозначений. Так, сами множества обозначают прописными буквами A, B, X, Y, а для обозначения элементов используют строчные буквы a, b, x, y. Если a – элемент множества A, то говорят, что a принадлежит A, и этот факт задают такой записью: aÎA. Если же a не является элементом множества A, то пишут: aÏA, и говорят, что a не принадлежит A.

Различают конечные множества и бесконечные. Конечное множество состоит из конечного числа элементов, причем неважно, известно это число или нет, главное, что оно существует. Общее число элементов в конечном множестве называют его мощностью. Количество элементов в бесконечном множестве подсчету не поддается, даже теоретически.

Задать конечное множество можно, просто перечислив его элементы. Например, множество X из n элементов: X={x₁, x₂,¼, x_n}. В частности, при n=1 имеем одноэлементное множество X={x₁}. Однако простое перечисление элементов множества неудобно для больших n и вовсе не годится для задания бесконечных множеств. Выход из этой ситуации – задать множество описанием свойств его элементов (с помощью характеристических свойств множества). Пусть все элементы x множества X обладают свойствами P(x). Тогда это множество задается такой конструкцией: X={x: P(x)}. Ее читают так: множество X, состоящее из элементов x таких, что каждый из них обладает свойствами P(x). Скажем, множество A={1, 2, 3, 4, 5} можно задать и так: A={x: xÎN и x<6}, где N – множество натуральных чисел. Еще пример. Отрезком [a,b] называется такое множество: [a,b]={xÎR: a£x£b}. Фразу эту можно прочесть так: отрезок [a,b] – это элементы x из множества R вещественных чисел, значения которых больше или равны a и меньше или равны b. А запись ]a,b[={xÎR: a<x<b} задает множество, называемое интервалом, а именно, элементы x из множества вещественных чисел такие, что их значения строго больше a и строго меньше b.

Если множество A является частью множества B, то говорят, что A есть подмножество B. Записывается это отношение множеств так: AÌB. А запись BÌA говорит о том, что B есть подмножество A.

Множества A и B называют равными, когда они состоят из одних и тех же элементов. На языке теории множеств это записывают так: A=B. Например, множества A={3,5,7,9} и B={7,3,9,5} состоят из одних и тех же элементов, значит, они равны.

Множества A и B равны тогда, когда одновременно верны оба утверждения:

если xÎA, то xÎB,

если xÎB, то xÎA.

Пример. Пусть A – множество всех четных положительных чисел, B – множество положительных чисел, каждое из которых есть сумма двух положительных нечетных чисел. Докажем, что A=B.

Проверим, выполняются ли указанные условия:

Пусть xÎA, то есть x – положительное четное число. Это значит, что x=2´k, где k – некоторое натуральное число. Преобразуем выражение для x: x=(2´k-1)+1, то есть представим x суммой двух положительных нечетных чисел 2´k-1 и 1. А это означает, что xÎB.

Пусть xÎB, то есть x=m₁+m₂, где m₁ и m₂ – положительные нечетные числа. Для них всегда можно найти такие натуральные числа k₁ и k₂, что m₁=2´k₁-1, а m₂=2´k₂-1. Тогда

x=2´k₁-1+2´k₂-1=2´(k₁+k₂-1)=2´k.

Значит, x – положительное четное число, поскольку k=k₁+k₂-1 – натуральное число. Следовательно, xÎA.

Итак, утверждение A=B (при заданных условиях) доказано.

Утверждение A=B верно и тогда, когда между ними одновременно имеют место отношения:

AÌB и BÌA.

Пример. Зададим множество W так:

W={М,Н,О,Ж,Е,С,Т,В,А}.

Вот некоторые из его подмножеств:

S1={Н,О,С}, S2={С,О,Н}, S3={М,А,Н,Е,Ж},

S4={ М,О,Н,Е,Т,А}, S5={Ж,Е,М,А,Н,С,Т,В,О}.

Как видим, S1=S2, а S4ÌW. Точно так S5ÌW. В то же время и WÌS5. Значит, W=S5.

Обычно в ходе исследования тех или иных множеств можно ввести в рассмотрение такое множество, которое включает в себя все допустимые в этом исследовании множества. Такое широкое множество называют универсальным и обозначают символом W. Любое из анализируемых множеств формируется из элементов универсального множества так. Формулируются характеристические свойства множества. Из элементов W выделяются те, которые обладают названными свойствами. Каждый из этих элементов клонируется. Совокупность таких клонов и образует нужное множество. Например, для множеств W, S1, S2, S3, S4, S5 (и многих других, им подобных) универсальным будет множество W прописных букв русского алфавита. И при формировании множеств S1 и S2 дважды клонируются элементы Н, О, С.

Для полноты картины удобно ввести в рассмотрение и пустое множество, в котором нет ни одного элемента. Обозначают пустое множество символом Æ.

1.2. Операции над множествами

В теории множеств рассматривают операции, которые позволяют из одних множеств получать другие. Другими словами, результатом любой операции над множествами будет новое множество, элементами которого являются клоны тех элементов W, которые отвечают определению данной операции.

Опишем основные из операций над множествами.

Пусть заданы множества A, B и W (рис.1.1,а). Перед выполнением операции нужно создать шаблон для ее результата (рис. 1.1,б). Пользуясь определением операции, на шаблоне выделяют ее результат сплошной границей и заливают (или штрихуют).

Объединение множеств. Эта операция – многоместная. Сформулируем ее определение для двух операндов (рис.1.1,в):

Объединением множеств A и B является новое множество C, состоящее из элементов множества A или элементов множества B.

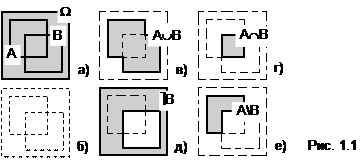
Обозначают объединение множеств так: C=AÈB.

Операцию объединения множеств A и B можно определить и указанием характеристических свойств элементов множества C:

C=AÈB={x: xÎA или xÎB}.

Эта запись означает, что множество C=AÈB образуют элементы x, а каждый из них входит или в A, или в B, или в оба эти множества.

Пример, A={1, 2, 3}, B={1, 3, 4}. Тогда C=AÈB={1, 2, 3, 4}. В последнем множестве элемент 2 принадлежит множеству A, элемент 4 – множеству B, а элементы 1 и 3 входят и в A, и в B.

Можно составить объединение любого числа множеств:

C=AÈBȼÈC.

Пересечение множеств. И эта операция многоместная. Для двух операндов она формулируется так (рис.1.1,г):

Пересечением множеств A и B называют новое множество D, которое состоит из элементов, общих для A и B.

Пересечение множеств A и B обозначают как D=AÇB.

Операцию пересечения множеств A и B можно определить и так:

D=AÇB={x: xÎA и xÎB}.

Эта запись означает, что множество D=AÇB образуют элементы x, а каждый из них входит и в A, и в B.

Пример. Пересечением множеств из предыдущего примера будет множество D=AÇB={1, 3}.

Два множества A и B называют непересекающимися, если AÇB=Æ. Если же AÇB¹Æ, то A и B – пересекающиеся множества.

Можно составить пересечение любого числа множеств:

D=AÇBǼÇC.

Дополнение множества до универсального. Эта операция одноместная, дополнить до универсального можно только одно множество (рис.1.1,д):

Дополнением множества B до универсального множества W называется новое множество F, включающее в себя элементы множества W, но без элементов множества B.

Эту операцию обозначают так: F=ùB.

Укажем характеристические свойства элементов множества F:

F=ùB={x: xÎW и xÏB}.

Пример. Имеем

W={Азия, Африка, Америка, Австралия, Антарктида}.

B={Австралия, Антарктида}.

Тогда

ùB=ù{Австралия, Антарктида}={Азия, Африка, Америка}.

Теперь можно сказать, что универсальным является такое множество W, для которого справедливы соотношения:

AÇW=A, AÈW=W.

Здесь A – произвольное множество.

Отметим, что результатом любой операции над множествами является новое множество. И это новое множество может быть операндом в другой операции. Так получают суперпозицию (цепочку) операций над множествами. При построении суперпозиций операций следует учитывать правило о приоритетах: наивысшим приоритетом обладает дополнение, следующий приоритет – у пересечения, самый низкий приоритет – у объединения множеств. Нарушить правило о приоритетах и задать иной порядок выполнения операций позволяют скобки. Выражение в скобках реализуется в первую очередь. Знание правила о приоритетах операций алгебры множеств позволяет заменить сложное выражение цепочкой более простых действий.

Пример. Имеем

Q=ù(AÈB)Çù(AÈC).

Заменим это выражение цепочкой таких действий:

P=AÈB, R=ùP, S=AÈC, T=ùS, Q=SÇT.

Объединение множеств, пересечение множеств и дополнение множества до универсального образуют функционально полную систему операций алгебры множеств.

Любое преобразование множеств можно представить суперпозицией операций объединения, пересечения и дополнения.

В теории множеств используют и другие операции. Например, двуместная операция разность множеств (рис.1.1,е):

Разностью множеств A и B называют множество G, в которое включены элементы множества A и не включены элементы множества B.

Обозначают разность множеств так: G=A\B.

Разность множеств A и B можно определить и так:

G=A\B={x: xÎA и xÏB}.

Выразим операцию G=A\B в терминах функционально полной системы операций:

G=A\B=AÇùB. (1.1)

На рис. 1.1,г множество A показано пунктиром. Видно, что пересечение множеств A и ùB образует множество A\B (рис. 1.1,е).

Дополнение множества A до универсального W можно представить такой разностью:

ùA=W\A.

1.3. Аксиомы и теоремы алгебры множеств

Для любых множеств A, B и C справедливы следующие аксиомы и теоремы (табл. 1.1). Здесь утверждения 1..5 и 1’..5’ – аксиомы алгебры множеств, остальные утверждения – суть некоторые из основных ее теорем. И аксиомы, и теоремы алгебры множеств объединим одним словом – тождества.

Таблица 1.1
	AÈB=BÈA			AÈBÈC=AÈ(BÈC)
1’	AÇB=BÇA		2’	AÇBÇC=AÇ(BÇC)
	AÈ(BÇC)=(AÈB)Ç(AÈC)			AÈÆ=A
3’	AÇ(BÈC)=(AÇB)È(AÇC)		4’	AÇW=A
	AÈùA=W			AÈW=W
5’	AÇùA=Æ		6’	AÇÆ=Æ
	AÈA=A			AÈ(AÇB)=A
7’	AÇA=A		8’	AÇ(AÈB)=A
	(AÇB)È(AÇùB)=A			ù(AÈB)=ùAÇùB
9’	(AÈB)Ç(AÈùB)=A		10’	ù(AÇB)=ùAÈùB
	ùW=Æ			ùùA=A
11’	ùÆ=W

Укажем на известную аналогию между приведенными аксиомами алгебры множеств и аксиомами школьной алгебры. Так, в теории множеств аксиомы 1 и 1’ называются коммутативными законами. Эти законы утверждают, что в операциях объединения и пересечения операнды можно располагать в любом порядке. Аксиомы 2 и 2^’ – это ассоциативные законы для множеств. Они свидетельствуют о том, что каждую из многоместных операций над множествами можно свести к последовательности двуместных операций. Аксиоме 3^’ в школьной алгебре отвечает дистрибутивный закон. А вот аксиоме 3 в школьной алгебре нет аналога. Тем не менее, аксиомы 3 и 3^’ алгебры множеств называются дистрибутивными законами для множеств. Эти законы задают правила раскрытия скобок (если двигаться от левой части равенства к его правой части) или же правило выноса за скобки подобных членов (если двигаться в обратном направлении).

Дата добавления: 2014-11-18