Элементы статистической обработки данных 5 страница

Вопросы и задачи для самоконтроля

1. Пояснить основные понятия математической логики:

«высказывание»,

«простое высказывание»,

«сложное высказывание».

2. Привести определения логических операций: отрицание, конъюнкция, дизъюнкция, импликация, равнозначность.

3. Сформулировать понятие функционально полной системы операций алгебры логики.

4. Сформулировать правило о приоритетах логических операций.

5. Следующие утверждения перевести на язык алгебры логики и для каждого из них построить таблицу истинности.

а) Уголовной ответственности подлежит лицо, совершившее преступление и достигшее ко времени его совершения шестнадцатилетнего возраста.

б) Лицо не подлежит уголовной ответственности за преступление, если оно добровольно и окончательно отказалось от доведения этого преступления до конца.

в) Преступление признается совершенным по небрежности, если лицо не предвидело возможности наступления общественно опасных последствий своих действий (бездействия), хотя при необходимой внимательности и предусмотрительности должно было и могло предвидеть эти последствия.

г) a<b или a=b;

д) если a>b, а b>c, то v=w;

6. Пояснить смысл свойства двойственности системы аксиом и теорем алгебры логики.

7. Составить таблицы истинности для следующих высказываний:

а) P®(P®Q);

б) P®ù(QÚR);

в) (P®(QÙR))Ú(ùPÙQ).

8. Пользуясь табл. 3.16, записать и упростить (если можно) ФАЛ для P, Q, R.

Таблица 3.16
x2	x1	x0	P	Q	R

9. Доказать истинность следующих утверждений:

а) ù(AÙùA)=1 – закон противоречия,

б) (A®ùA)®ùA – принцип приведения к абсурду,

в) AÙ(A®B)®B – правило извлечения следствия,

г) (A®B)=(ùB®ùA) – закон контрапозиции,

д) ((A®B)®A)®A – закон Пирса,

е) ((A®B)Ù(B®C))®(A®C) – закон силлогизма.

10. Выполнить ДКЗ: Тест 3. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ.

Время содержания лица под стражей до судебного разбирательства засчитывается в сроки лишения свободы, содержания в дисциплинарной воинской части и ареста из расчета один день за один день, ограничения свободы – один день за два дня, исправительных работ и ограничения по военной службе – один день за три дня, а в срок обязательных работ – из расчета один день содержания под стражей за восемь часов обязательных работ.

(УК РФ, Ст. 72, ч.3)

РАЗДЕЛ II
ОСНОВЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА

Глава 4. ФУНКЦИИ

4.1. Понятие функции

Пусть X и Y – непустые числовые множества (рис.4.1).

Функцией из X в Y называют закон f, по которому каждому элементу xÎX ставится в соответствие единственный элемент yÎY.

Элемент xÎX называют аргументом, а элемент yÎY – значением функции f. Множество X называется областью определения функции f (областью ее существования), а множество Y – областью значений функции f. Область определения и область значений функции f обозначим как D_f и E_f, соответственно.

Задать функцию – значит указать область ее определения D_f, область ее значений E_f и сформулировать закон (правило) f о том, как для каждого заданного x получить свой y.

Известны следующие способы задания функций:

ü аналитический,

ü табличный,

ü графический.

Задать функцию аналитически – это записать ее формулой. Если множества X и Y определены, то функцию из X в Y задают записью вида y=f(x). Это наиболее компактный, удобный и универсальный способ задания функции. Формулой задают набор вычислительных операций над x, выполнив которые получают y. Обычно по формуле можно найти и область определения функции, и область ее значений. Когда мы читаем запись

y=0.25´x³, (4.1)

нам ясно, что эта функция ставит в соответствие каждому числу x четвертую часть его куба. Эта функция определена на всей числовой оси: xÎR, и область ее значений – тоже множество вещественных чисел yÎR.

Конечно, для обозначения самой функции, ее аргумента и ее значений кроме букв f, x, y можно применить любые другие буквы, а может быть и их сочетания (если не пропускать, как это мы и делаем, знак ´ умножения в записях произведений).

Табличный способ задать функцию состоит в том, что значения аргумента записывают в одной строке (в одном столбце), а значения функции – в другой строке (в другом столбце). Правило f здесь предельно простое: под каждым (рядом с каждым) значением табличного аргумента xt_i – свое значение табличной функции yt_i.

Таблицу можно построить по аналитическому выражению функции. Часто в таблицу сводят результаты эксперимента, каждый из которых не имеет соответствующего аналитического описания.

Если функция задана аналитически, то процедура построения ее таблицы состоит в следующем.

Область определения функции ограничивают отрезком [a,b]. На этом отрезке задают сетку

a=xt₀,xt₁,xt₂,¼,xt_i,xt_i+1,¼,xt_n=b

с равномерным шагом h= 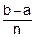, где n – объем таблицы. Понятно, что xt_i=a+i´h, i= 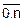. Это содержимое первой строки будущей таблицы.

Для каждого значения xt_i по формуле yt_i=f(xt_i) вычисляют отсчеты табличной функции. Так получают вторую строку таблицы. Удобно бывает дополнить таблицу еще одной (верхней) строкой с номерами 0, 1,…, i, i+1,…, n ее отсчетов.

Пример. Построим таблицу по аналитическому выражению (4.1).

Ограничимся отрезком [0,2] и n=4. Имеем:

h= 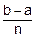=0.5, xt_i=a+i´h, yt_i=0.25´(xt_i)³.

В результате получим табл.4.1.

Таблица 4.1
i
xti	0.0	0.5	1.0	1.5	2.0
yti	0.00	0.03	0.25	0.84	2.00

Таблично заданную функцию будем представлять такой конструкцией: {xt_i,yt_i}.

Аналитический и табличный способы задания функции недостаточно наглядны. Это обусловливает применение графического способа задания функции. Обычно график дополняет другие способы задания функции. Строится график всегда по таблице чаще всего в декартовых координатах. Декартова система координат образована двумя взаимно перпендикулярными прямыми. Горизонтальная прямая – это ось абсцисс 0x, вертикальная прямая – ось ординат 0y. Точка пересечения осей служит началом координат. По каждой из осей задают шкалу. Цена делений по оси 0x равна или кратна шагу таблицы h. Цену делений по оси 0y вычисляют по данным во второй строке таблицы так, чтобы получить удобочитаемые числа по оси 0y.

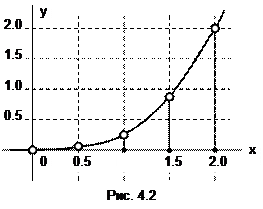
Итак, сначала строится таблица {xt_i,yt_i}. По данным этой таблицы строится точечный график. Каждой паре чисел xt_i и yt_i из колонки таблицы номер i на координатной плоскости ставят в соответствие точку (xt_i,yt_i). Эти точки на графике соединяют плавной кривой.

На рис.4.2 показан график, построенный по табл. 4.1. Здесь кружочками показаны точки табличной функции, и они соединены плавной линией.

В данном разделе мы ограничим наши интересы только такими функциями, каждая из которых не имеет особенностей в области ее определения.

Обратная функция. Пусть функция f имеет для y ровно столько же разных значений, сколько значений имеет и ее аргумент x. Отсюда следует, что уравнение f(x)=y всегда можно разрешить относительно x и записать x=g(y).

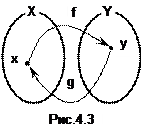
Функция g, которая ставит в соответствие каждому элементу yÎY единственный элемент xÎX, такой, что y= f(x), называется обратной к функции f (рис.4.3).

Функцию f называют прямой (исходной). Область определения обратной функции совпадает с областью значений исходной функции 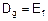и наоборот . Функция, обратная к g, есть прямая функция f. Значит, функции f и g – взаимно обратные.

Пример. Пусть исходная функция y=2^x. Построим ее график. Для этого составим табл.4.2, построим точечный график и соединим точки, заданные таблицей, плавной линией (рис.4.4). Как видим, эта функция возрастает на всей числовой оси и ограничена снизу осью абсцисс.

	Таблица 4.2
f(x)	x	-3	-2	-1				y	g(x)
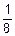
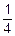
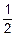
y							x

А теперь найдем функцию, обратную к y=2^x, и построим ее график в тех же (!) координатах, что и график прямой функции. Для этого в записи исходной функции поменяем местами x и y: x=2^y. Из этого уравнения найдем y: y=log₂(x). Это и есть функция, обратная к исходной y=2^x. Таблицу обратной функции получают из таблицы исходной, поменяв в ней местами обозначения строк (табл. 4.2). По этой таблице и строим график обратной функции (рис.4.4). Как видим, это функция – возрастающая при x>0, и она не ограничена.

Данный пример иллюстрирует общее свойство взаимно обратных функций: графики исходной и обратной функций имеют осью симметрии прямую y=x (когда масштабы по осям координат одинаковы).

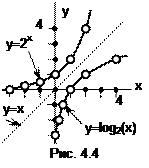
Сложная функция. Пусть заданы функции s=g(x) и z=f(s) такие, что область определения функции f совпадает с областью значений функции g (рис.4.5). Функция g отображает множество X на множество S, а функция f отображает множество S на множество Z. Эти два отображения вместе задают новое отображение h множества X на множество Z. Такое отображение и называется сложной функцией (суперпозицией функций f и g):

z=f(g(x))=h(x).

Например,

s=g(x)=sin(x), f(s)=s².

Тогда

z=f(g(x))=(sin(x))²=h(x).

Если же

s=g(x)=x², а f(s)=sin(s),

то

z=f(g(x))=sin(x²)=h(x).

В суперпозиции функций f(g(x)) функцию s=g(x) называют вложенной, а функцию f(s) называют внешней.

На практике проблема состоит в том, что заданной является функция h(x), а нужно бывает найти и выделить вложенную и внешнюю функции. Для этого поступают так. Мысленно задают значение аргумента x и фиксируют те действия в h(x), которые выполняются над ним в первую очередь. Эти действия и образуют вложенную функцию s=g(x). Далее определяют те действия в h(x), которые производятся над s – результатом вложенной функции. Они и составляют внешнюю функцию z=f(s).

Например, имеем

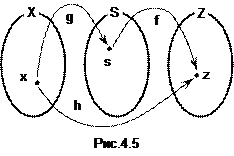
h(x)= .

Здесь в первую очередь x возводят в куб, а из полученного результата извлекают корень пятой степени, значит,

s=g(x)=x³, z=f(s)= .

Можно составить суперпозицию из трех и более функций. Например,

h(x)= 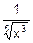. s=x³, z= , v= .

4.2. Аппроксимация функций

Аппроксимация – это замена функции f(x) на отрезке [a,b] подходящей формулой j(x) такой, чтобы погрешность замены ôj(x)-f(x)ô не превышала бы заданных значений.

Для выполнения аппроксимации функцию f(x) на отрезке [a,b]представляют таблицей {xt_i,yt_i}. Для этого отрезок [a,b] разбивают на n частей и получают набор значений аргумента табличной функции a=xt₀, xt₁, xt₂,¼, xt_k, xt_k+1,¼ xt_n-1, xt_n=b, а по формуле f(x) вычисляют набор отсчетов табличной функции yt_i=f(xt_i), i= (число n – объем таблицы). По данным этой таблицы {xt_i,yt_i} и подбирают подходящую формулу j(x).

Когда и для чего применяют аппроксимацию?

Первое, когда f(x) – сложная формула, и получение большого массива величин y=f(x) требует значительных вычислительных затрат. Тогда формулу f(x) используют только для построения таблицы {xt_i,yt_i} объемом n, а основной массив значений y вычисляют по более простой формуле j(x).

Второе, когда функция задана только таблицей {xt_i,yt_i}, полученной в ходе исследований, эксперимента, испытаний. Однако и для таких табличных функций бывает необходимо знать значения y для любых x¹xt_i. Формула j(x), построенная по данным таблицы, оказывается единственным средством для решения такой задачи.

Вычисление y по формуле j(x), когда x лежит внутри таблицы (xt₀£x£ xt_n), называют интерполяцией функции {xt_i,yt_i}. Когда же x лежит вне таблицы, определение значения y=j(x) называют экстраполяцией функции {xt_i,yt_i}. Если x<xt₀, то имеет место экстраполяция назад, если же x>xt_n, экстраполяция вперед. Примером экстраполяции вперед будет прогноз показателей преступности на следующий год по результатам измерений ее параметров в предыдущие годы.

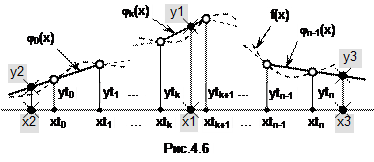
Самый простой способ аппроксимации функции основан на том, что каждые две соседние точки на графике табличной функции (xt_k,yt_k) и (xt_k+1,yt_k+1) (k= ,) соединяют прямой линией (рис. 4.6). Такая аппроксимация называется линейной. Уравнение отрезка прямой j_k(x) и будет подходящей формулой, по которой вычисляется y для любого xÎ[xt_k, xt_k+1]. Поскольку k= , при линейной аппроксимации имеем n уравнений вида j_k(x), то есть n подходящих формул с номерами от 0 до n-1 (рис. 4.6). Отметим, что номер k формулы и номер отрезка совпадают с номером точки, в которой этот отрезок начинается.

Формулу для j_k(x) получим так. На рис. 4.7 показан фрагмент графика табличной функции на отрезке [xt_k, xt_k+1]. Зададим на этом отрезке значение x и отметим на отрезке прямой, соединяющей точки y_k и y_k+1, значение y=j_k(x). Как видим,

y=j_k(x)=y_k+Dy.

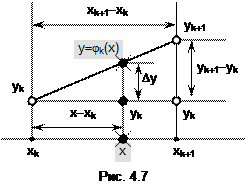
Величину Dy найдем из подобия прямоугольных треугольников, один из которых имеет катеты Dy и x-x_k, а другой – катеты y_k+1-y_k и x_k+1-x_k:

= .

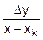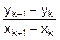Отсюда

Dy= .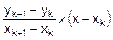

Подставив найденное Dy в выражение y=j_k(x)=y_k+Dy, получим искомое

y=j_k(x)=yt_k+ 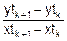´(x-xt_k), (4.2)

Напомним, что здесь k= , то есть формула (4.2) и есть уравнение любого из n отрезков на рис. 4.6.

Две прямые на рис. 4.6 – особые. Формулу для самой левой из них j₀(x) используют не только для вычисления значений y на отрезке [xt₀,xt₁], но и для всех x<xt₀, то есть для экстраполяции назад. Формулу для самой правой прямой j_n-1(x) используют и для экстраполяции вперед, то есть для вычисления значений y при всех x>xt_n. На рис. 4.6 нахождение значения y1 для x1: y1=j_k(x1) – суть интерполяция, значения y2 для x2: y2=j₀(x2) – экстраполяция назад, значения y3 для x3: y3=j_n-1(x3) – экстраполяция вперед.

Номер k уравнения той прямой j_k(x), на которой лежит искомое значение y, определяют по заданному x так:

k(x)= 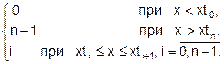(4.3)

В найденную формулу j_k(x) подставляют заданное значение x, значения yt_k, yt_k+1, xt_k, xt_k+1 из таблицы {xt_i,yt_i} и вычисляют искомое значение y.

Ломаная j_k(x) (k= ) отличается от графика функции f(x), по которой построена таблица {xt_i,yt_i}. Поэтому значение y=j_k(x), полученное по аппроксимирующей формуле, содержит ошибку. Оценить эту ошибку можно, сравнив результат аппроксимации с точным значением y_T=f(x), скажем, так:

D%= 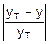´100%.

Полагаем, что y_T¹0.

Пример. Данные о количестве зарегистрированных преступлений П в городе Б за последние годы Г содержит табл.4.3. Восполнить недостающие сведения о количестве П за 2010 год и найти ожидаемое значение П в 2013 году.

Таблица 4.3
i
Гтi
Птi

По табл. 4.2 строим график (рис. 4.7).

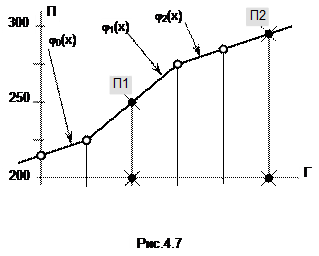
По формуле (4.3) для Г1=2009 находим, что k=1. Подставляем это значение k в формулу (4.2), поменяв в ней обозначения переменных, и вычисляем искомое значение П1:

П1=Пт₁+ ´(Г1-Гт₁)=

=226+ 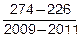´(2010-2009)=250.

Проверим полученный результат, задав точку (Г1,П1) на графике (рис. 4.7).

Значение П2 можно получить прямо по графику, для чего задать точку Г2=2013 на оси абсцисс и найти точку П2 на соответствующей прямой (рис. 4.7). Тем не менее, находим k=2 для Г2=2013, и

П2=Пт₂+ 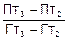´(Г2-Гт₂)=

=274+ 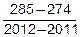´(2013-2011)=285.

Отметим, что в этой задаче функция задана только таблицей, и для оценки погрешностей данных нет.

4.3. Предел функции

Отметим, что расстояние между числами p и q на числовой оси суть модуль разности этих чисел ½p-q½.

Зафиксируем на числовой оси точку a и положим, что переменная x меняется так, что каждое его следующее значение будет ближе к числу а, чем предыдущее. И какое бы малое число d>0 ни назначить, настанет момент, когда будет выполнено условие ½x-a½<d, то есть расстояние от x до a будет меньше чем d. И последующие изменения x никогда не нарушают это условие. Про такое поведение x говорят: x стремится к a, и этот факт обозначают конструкцией x®a.

Число A называется пределом функции y=f(x) при x, стремящемся к a, если для любого наперед заданного положительного e найдется такое положительное d, что расстояние между y и A на оси ординат будет меньше чем e, а расстояние между x и a на оси абсцисс будет меньше чем d.

Записывается данное утверждение так:

.

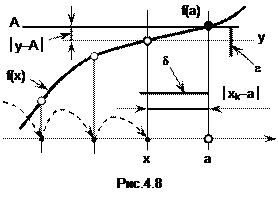
Смысл этого определения поясняет рис.4.8. Как видим, значения функции y=f(x) приближаются к числу A (расстояние ½y-A½ уменьшается), когда значения аргумента x приближаются к a (расстояние ½x-a½ уменьшается). Это означает, что для любого числа e>0 наступит момент, когда будет выполняться неравенство ½y-A½<e. При этом можно назвать такое число d>0, когда выполняется неравенство ½x-a½<d. Совместное выполнение этих неравенств и означает, что число A является пределом функции f(x) когда x стремится к a.

Тот факт, что число A является пределом функции f(x) при x®a, устанавливают до того момента, когда расстояние ½x-a½ окажется равным нулю, то есть x достигнет значения a. Поэтому в теории пределов вместо неравенства ½x-a½<d оперируют с системой неравенств 0<½x-a½<d.

Пример. Рассмотрим бесконечную последовательность точек на числовой оси x={x₀, x₁, x₂,¼, x_k,¼}:

x₀=2- =1, x₁=2- =1.5,

x₂=2- =1.75, …, x_k=2- , …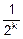

Любое из этих чисел меньше a=2. Но по мере роста значения k увеличивается и количество таких чисел, которые все теснее и теснее скапливаются около точки a=2. Расстояние ½x_k-2½ уменьшается и с каждым новым k может стать меньше любого наперед заданного числа d>0, то есть x®2.

Каждому значению x из последовательности x₀, x₁,¼, x_k,¼ отвечает свое значение функции y=f(x). Например, значения функции y=x² составят такую бесконечную последовательность:

y₀=1²=1, y₁=1.5²=2.25,

y₂=1.75²=3.0625, ¼, y_k= 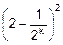, ¼

Как видим, каждое следующее значение y_k все ближе к A=4 и с каждым новым k разность ½y_k-4½ может стать меньше любого наперед заданного числа e>0. Положим e=2^-3@0.13 и найдем d. Из условия

½y_k-4½= 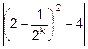= @2^-k+2<2^-3

находим, что неравенство ½y_k-4½<2^-3 выполняется при k>5.

Далее ½x_k-2½= =2^-k. При k>5 получим, что ½x_k-2½<2^-5. Значит, d=2^-5@0.03.

Таким образом, совместное выполнение неравенств ½y_k-4½<e=2^-3 и 0<½x_k-2½<d=2^-5 позволяет сделать вывод о том, что

.

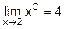И этот факт был установлен, несмотря на то, что равенство x_k=2 не достигается ни при каком сколь угодно большом значении k.

Говорят, что x®+¥, если x меняется так, что каждое следующее его значение становится больше предыдущего. И какое бы большое положительное число M ни назначить, наступит момент, когда x окажется больше M, и далее это отношение между ними не меняется. Тогда утверждение 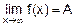означает следующее: для любого e>0 найдется такое M>0, что½f(x)-A½<e при x>M.

Говорят, что x®-¥, если x меняется так, что каждое следующее его значение становится меньше предыдущего. И какое бы большое положительное число M ни назначить, наступит момент, когда x окажется меньше -M, и далее это отношение между ними не меняется. Тогда утверждение 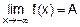означает следующее: для любого e>0 найдется такое M>0, что½f(x)-A½<e при x<-M.

Пусть имеются функции f(x) и g(x), которые имеют конечные пределы в точке x=a (a – величина конечная или бесконечная):

, .

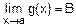При вычислениях пределов используют следующие их свойства:

1) 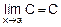, C=const.

2) .

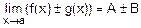3) .

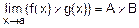4) .

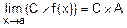5) 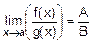, когда g(x)¹0 для a-d<x<a+d, а B¹0.

Предложим читателю дать словесное толкование каждому из этих свойств.

Практически всегда при вычислении предела функции в первую очередь делают прямую подстановку x=a в формулу для f(x) с тем, чтобы найти A=f(a), то есть (см. рис. 4.8)

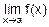=f(a)=A.

Дата добавления: 2014-11-18