Элементы статистической обработки данных 2 страница

Обратим внимание на парные утверждения табл. 1.1. Тождество номер J^’ получают из парного тождества номер J (J= 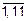) путем замены в нем символа È на символ Ç (и наоборот), символа W на символ Æ (и наоборот). Говорят, что тождества J и J^’ дуальны или двойственны друг другу.

Для любых дуальных выражений справедливо утверждение: если выражение J верно, то верно и двойственное ему выражение J^’. Поэтому нет нужды доказывать верность каждого из дуальных выражений, достаточно доказать лишь одно из них. Это утверждение называют принципом двойственности.

Ради полной симметрии в выражениях 1..10 и 1^’..10^’ скобки проставлены и там, где без них можно было бы обойтись по правилу о приоритетах.

Аксиомы 1..5 и 1^’..5^’ средствами теории множеств не доказываются, но подтверждаются проверкой. Проверим, например, верность утверждения 3. Отправляемся от его левой части. Пусть xÎAÈ(BÇC). Тогда по определению для объединения имеем xÎA или xÎ(BÇC). Но если xÎA, то x принадлежит и объединению A с любым другим множеством. В частности xÎAÈB и xÎAÈC. Значит, x принадлежит пересечению этих множеств, то есть xÎ(AÈB)Ç(AÈC), а это – правая часть утверждения 3. А если xÎ(BÇC), то из определения для пересечения множеств вытекает, что xÎB и xÎC. Значит, x принадлежит и объединению каждого из множеств B и C с любым другим множеством, в частности с A: xÎ(AÈB) и xÎ(AÈC). Тогда снова имеем xÎ(AÈB)Ç(AÈC). Так, двигаясь от левой части 3, приходим к его правой части. Аналогично, двигаясь от правой части 3, можно прийти к его левой части. Поскольку утверждение 3 верно, верно и утверждение 3’.

Тождества 1..11, 1^’..11^’ и 12 используют для доказательства тех или иных утверждений относительно множеств, для упрощения выражений алгебры множеств.

Пример. Докажем следующее утверждение:

если AÈB=W и AÇB=Æ, то B=ùA.

Номера тождеств, которые используются в цепочке наших рассуждений, будем заключать в угловые скобки. Итак,

B=á4ñ=BÈÆ=á5^’ñ=BÈ(AÇùA)=á3ñ=(BÈA)Ç(BÈùA)=

=á1 и условие AÈB=Wñ=WÇ(BÈùA)=á5ñ=

=(AÈùA)Ç(BÈùA)=á1ñ=(ùAÈA)Ç(ùAÈB)=á3ñ=

=ùAÈ(AÇB)=áусловие AÇB=Æñ=ùAÈÆ=á4ñ=ùA,

что и требовалось доказать. Читателю предложим проиллюстрировать наши рассуждения рисунком.

Вопросы и задачи для самоконтроля

1. Поясните понятие множества, какие отношения бывают между множествами. Дайте определение универсального множества, пустого множества.

2. Поясните смысл операций алгебры множеств:

§ объединение множеств,

§ пересечение множеств,

§ дополнение множества до универсального,

§ разность множеств.

3. Пояснить понятие и основное свойство функционально полной системы операций алгебры множеств. Изложить правило о приоритетах операций алгебры множеств.

4. Пользуясь табл. 1, пояснить принцип двойственности тождеств алгебры множеств.

5. Разложить каждое из следующих выражений в цепочку простых действий над множествами:

а) Q=ù(AÇBÇC)Ç((AÈB)Ç(AÈC)Ç(BÈC)),

б) Q=(AÈBÈC)Ç(ù(AÇB)Èù(AÇC)Èù(BÇC)),

в) Q=(AÇBÇC)È(ù(AÈB)Çù(AÈC)Çù(BÈC)),

г) Q=ù(AÈBÈC)È((AÇB)È(AÇC)È(BÇC)).

На рис. 1.2 заданы универсальное множество W, множества A, B, C (на номера 1…8 пока не обращаем внимания). Заштриховать результат каждого из цепочки выполняемых простых действий.

6. Доказать утверждения алгебры множеств:

а) AÈ(ùAÇB)=AÈB, б) (AÇB)È(AÇùB)=A,

в) ù(AÈB)=(ùAÇùB), г) ù(AÇB)=(ùAÈùB).

7. Универсальное множество W его подмножествами A, B, C (рис.1.2) разбивается на восемь непересекающихся областей 1..8. Описать в терминах операций алгебры множеств каждую из этих областей.

8. На рис. 1.2 убрать все номера и заштриховать каждую из областей, которые определяются соотношениями:

а) ù(AÇBÇC), б) ù(AÈBÈC),

в) AÈù(BÇC), г) ù(AÈ(BÇC)).

9. Составлены два списка правовых документов по проблеме «Информационная безопасность» (список ИБ) и по проблеме «Защита информации» (список ЗИ). Записать те операции над множествами ИБ и ЗИ, которые позволят:

а) составить полный перечень документов (без повторов).

б) выделить документы, включенные и в список ИБ, и в список ЗИ,

в) выделить документы, включенные только в список ИБ,

г) выделить документы, включенные только в список ЗИ,

10. Выполнить ДКЗ: Тест 1. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ.

Глава 2. ЧИСЛА

2.1. Системы счисления

Число – древнейшее из математических понятий. Оно родилось в ответ на нужды практической, хозяйственной деятельности человека. Началось все с натуральных чисел, которые появились в связи с необходимостью подсчитывать отдельные предметы (скот, рабов, воинов и др.). Торговля, прибыль и долги привели к использованию целых чисел (положительных и отрицательных). Дальнейшее усложнение производства, необходимость измерять и вычислять длины отрезков прямых, площади прямоугольников и кругов породили рациональные и вещественные числа.

Выдающимся мыслительным актом, началом абстрактного мышления было отделение числа от предмета счета, когда в вычислениях стали оперировать только с самими числами. А это потребовало умения записывать числа.

Совокупность приемов и правил, устанавливающих взаимно однозначное соответствие между числом и его записью, называют системой счисления (нумерацией).

К примеру, на рис. 2.1. для одного и того же числа тринадцать приведены записи в римской, десятичной и двоичной нумерациях.

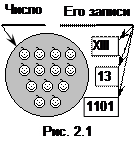Сегодня практически повсеместно применяют десятичную позиционную систему счисления. Слово десятичная означает, что счет предметов ведут десятками, а число десять называют основанием системы счисления. В десятичной системе счисления для записи чисел применяют десять арабских цифр {0,1,...,9}. Смысл слова позиционная поясним примером. Записи 333 отвечает число, заданное такой суммой:

3´10²+3´10¹+3´10⁰.

Как видим, в записи использована одна цифра 3. Но ее вес (множитель при степени десятки в сумме) зависит от места, которое эта цифра занимает в записи числа. Самая левая цифра весит 10²=100, а самая правая тройка имеет вес 10⁰=1. Нередко пишут, что

3´10²+3´10¹+3´10⁰=333,

то есть отождествляют число с его записью. Это связано с тем, что на практике, как было сказано выше, чаще оперируют не с самими числами, а с их записями.

Итак, каждое число представляют суммой степеней десятки, коэффициентом у каждой степени будет та или иная из десятичных цифр. А запись числа получают, выписав подряд коэффициенты суммы. Позиция, которую занимает цифра в записи числа, называется разрядом. Для того чтобы подчеркнуть свойство позиционности удобно пронумеровать разряды в записи числа в соответствии со степенями основания системы счисления: 3₂3₁3₀. Разряды с номерами (весами), б о льшими, чем у данного, называются старшими по отношению к нему, а разряды, номера (веса) которых меньше чем у данного, называются младшими.

Причина столь широкого распространения десятичной системы счисления отнюдь не математического свойства. Десять пальцев рук – вот природный инструмент счета, которым человек пользуется с древнейших времен. История знает и другие, отличные от десятичной системы счисления. Индейцы Северной Америки считали двадцатками, используя пальцы и рук, и ног. Англичане до сих пор сопротивляются введению метрической системы мер, у них двенадцать дюймов составляют один фут. В этом случае счет ведется дюжинами помощью фаланг четырех пальцев руки (без большого пальца).

В компьютерах числа представляются в двоичной системе счисления (компьютер считает двойками). Здесь основание системы счисления – два, цифры для записи двоичных чисел {0,1}. Однако лет за двести пятьдесят до появления первых компьютеров Лейбниц (юрист, как мы знаем) показал возможность записывать любое число символами 0 и 1. Он был активным пропагандистом двоичной системы счисления как самой простой и согласованной с алгеброй логики, там значение высказывания обозначают или 0 (ложь), или 1 (истина).

В двоичной системе счисления каждое число представляют суммой степеней двойки, коэффициентом у каждой степени будет или 0, или 1. Запишем, к примеру, десятичное число 333 в двоичной системе счисления:

333=1´2⁸+0´2⁷+1´2⁶+0´2⁵+0´2⁴+1´2³+1´2²+0´2¹+1´2⁰=

=1₈0₇1₆0₅0₄1₃1₂0₁1₀.

Опишем такую процедуру преобразования 10®2, когда не нужно формировать сумму степеней двойки.

Сначала составим таблицу первых степеней двойки (табл. 2.1, колонки n и 2ⁿ).

В общем случае десятичное число A представляется такой двоичной записью:

A=a_na_n-1¼a_ia_i-1¼a₁a₀, (2.1)

Таблица 2.1
2^n	n	n(2)	n(16)
			A
			B
			C
			D
			E
			F

где a_k={0,1}, k= .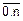

Преобразование 10®2.

§ Начинаем с того, что с помощью табл. 2.1 для заданного A находим такое n, когда выполняются условия: 2ⁿ£A<2ⁿ⁺¹. Так мы фиксируем номер n старшего разряда в искомой двоичной записи (2.1), а значит, и старшую цифру этой записи a_n=1_n.

§ Вычтем из A число 2ⁿ, которое отвечает полученной единице 1_n. Эту разность снова обозначим как A. Для этого нового A проверяем, содержится ли в нем число 2^n-1. Если число 2^n-1 входит в A, то a_n-1=1_n-1, в противном случае a_n-1=0_n-1. Так получим цифру в разряде номер n-1 искомой записи.

§ Если a_n-1=1_n-1, то вычитаем из A число 2^n-1, разность снова обозначим как А и переходим к разряду номер n-2. Если же a_n-1=0_n-1, то к разряду номер n-2 переходим без вычитания 2^n-1 из A.

§ Повторяем описанные действия до тех пор, пока не найдем цифру a₀.

Таблица 2.2
A=		=	17	06	15	14	13	12	01	00
	-128
A=
	-32
A=
	-16
A=

Найдем, для примера, двоичное изображение для десятичного числа A=188.

Пользуясь табл. 2.1, действуем в соответствии с описанием процедуры преобразования 10®2. Решение показано в табл. 2.2.

Отметим попутно, что после того, как записана цифра a₄ (у нас это 1₄), а очередной остаток A£15 (у нас это A=12) остальные четыре цифры a₃a₂a₁a₀ искомой записи получим из колонки n₍₂₎ табл. 2.1 как четырехразрядное двоичное изображение последнего остатка A=12. В нашем случае это комбинация 1₃1₂0₁0₀.

Преобразование 2®10. Это преобразование выполняют так. Нумеруют, начиная с нуля, разряды двоичной записи справа налево, а потом записывают полином степеней двойки, сумма которого и будет десятичным эквивалентом заданного двоичного числа. Например,

1010101=1₆0₅1₄0₃1₂0₁1₀=

=1₆´2⁶+0₅´2⁵+1₄´2⁴+0₃´2³+1₂´2²+0₁´2¹+1₀´2⁰=85.

Двоичные записи даже не очень больших чисел слишком длинные. В документации по компьютерам вместо длинных двоичных записей применяют шестнадцатеричные, которые оказываются вчетверо короче. В колонке n₍₁₆₎ табл. 2.1 приведены цифры шестнадцатеричной системы счисления.

Преобразования 2®16. Эта процедура никаких вычислений не требует и выполняется так. Убирают, если это нужно, нумерацию разрядов двоичной записи. Потом, двигаясь справа налево, разбивают двоичную запись на группы по четыре разряда в группе. Самую левую группу при необходимости дополняют нулями до четырех разрядов. Далее каждую четверку двоичных цифр заменяют одной шестнадцатеричной (см. две правые колонки табл. 2.1). Например,

1₈1₇1₆0₅1₄0₃1₂0₁1₀=|0001|1101|0101|=1D5.

Преобразование 16®2. А это преобразование выполняют в обратном порядке: каждую шестнадцатеричную цифру заменяют четверкой двоичных:

F72=1111 0111 0010.

Преобразование 16®10. Для того чтобы узнать, что скрывается за шестнадцатеричной записью, выполняют преобразование 16®10. Для этого сначала нумеруют разряды шестнадцатеричной записи, начиная с нулевого правого. А потом записывают и вычисляют соответствующую сумму степеней шестнадцати, в которой коэффициентами у степеней шестнадцати будут десятичные эквиваленты шестнадцатеричных цифр:

1D5=1₂D₁5₀=1₂´16²+13´16¹+5´16⁰=469.

Позиционные системы счисления обладают тем существенным достоинством, что в них весьма просто выполнять арифметические операции. Сложение, вычитание и умножение выполняются столбиком, путем поразрядных действий над цифрами в записях чисел. Деление выполняется углом, но каждую цифру частного получают опять-таки путем поразрядных операций над остатками. То или иное применение находят и непозиционные системы счисления. Классическим примером непозиционной системы считается римская нумерация. В ней значение цифры не зависит от ее позиции в записи числа. Так, число 333 в римской системе счисления задается записью CCCXXXIII. Здесь цифра C весит 100, где бы она ни стояла, и правила выполнения поразрядных операций здесь не действуют.

2.2. Классы чисел

Как мы знаем, все числа разделены на четыре класса:

натуральные числа – множество N,

целые числа – множество Z,

рациональные числа – множество Q,

вещественные числа – множество R.

При этом имеет место такая цепочка включений одного множества в другое:

NÌZÌQÌR.

Вещественные числа. Из перечисленных классов это самый широкий класс чисел. Например, с глубокой древности известно число p, которое выражает отношение длины окружности к ее диаметру. Еще одно широко известное в математике вещественное число e – основание натуральных логарифмов.

Вещественные (действительные) числа образуют сплошной массив точек на числовой прямой. Расстояние между числами (точками на прямой) бесконечно мало. Поэтому каждое вещественное число д о лжно было бы представлять записью с бесконечно длинной дробной частью.

Любая арифметическая операция над вещественными операндами имеет результатом вещественное же число. Говорят, что класс вещественных чисел замкнут относительно всех арифметических операций.

Укажем на такой математический феномен. Бесконечная цепь девяток в записи числа, начинающаяся с разряда номер k, равна единице в соседнем старшем разряде номер k+1:

0.0000009999¼=0.0000010000¼ (k=-7, k+1=-6),

09999999.999¼=10000000.000¼ (k=6, k+1=7).

Действительно, записи из бесконечной цепочки девяток отвечает сумма бесконечной геометрической прогрессии со знаменателем 10^-1:

9_k9_k-19_k-2¼=9_k´10^k+9^k-1´10^k-1+9_k-2´10^k-2+¼=

= =10^k+1=1_k+1´10^k+1.

Рациональные числа. На практике работать с вещественными числами невозможно хотя бы потому, что для записи чисел отводится ограниченное место. Числа, записи которых имеют конечную длину, образуют класс рациональных чисел. И этот класс чисел тоже замкнут относительно всех арифметических операций.

В общем случае рациональное число A изображается такой записью:

A=a_na_n-1¼a₀.a_-1a_-2¼a_-ka_-k-1a_-k-2¼a_-m.

Здесь a_na_n-1¼a₀ – целая часть числа, a_-1a_-2¼a_-ka_-k-1a_-k-2¼a_-m – его дробная часть. Как видим, все разряды записи числа (и дробной части тоже) пронумерованы по степеням десятки (разряд номер (-1) имеет вес 10^-1, разряд номер (-2) – вес 10^-2 и т.д.). Обычно целая часть числа отделяется от его дробной части запятой. В компьютерной математике (с которой мы будем иметь дело на практике) разделителем является десятичная точка. Этим разделителем мы и пользуемся.

На числовой прямой рациональные числа представлены точками, которые разделены расстоянием в 10^-m, где m – номер младшего разряда в записи чисел. Другими словами, расстояние между двумя соседними рациональными числами на числовой оси равно 1´10^-m, а именно, единице младшего разряда в из записях.

Бесконечные записи вещественных чисел, да и просто длинные записи рациональных чисел приходится укорачивать. Делается это по правилу округления десятичных дробей. Сформулируем это правило.

Пусть m-разрядную десятичную дробь

A=0.a_-1a_-2¼a_-k a_-k-1a_-k-2¼a_-m (2.2)

требуется округлить до k разрядов после точки.

Самое простое – это отбросить содержимое лишних младших разрядов (в записи (2.2) они залиты серым цветом):

A@A_усеч=0.a_-1a_-2¼a_-k.

Однако просто не всегда хорошо. В худшем случае во всех отброшенных разрядах могут оказаться девятки:

DA_max=a_-k-1a_-k-2¼a_-m=9_-k-19_-k-2¼9_-m´10^-k=1_-k´10^-k.

Значит, этот способ округления характеризуется такой максимальной абсолютной погрешностью

DA_max=1_-k´10^-k=0.0_-10_-2¼1_-k

(говорят, что DA_max равна единице младшего из оставшихся разрядов в записи числа A_усеч).

Для уменьшения погрешности округления действуют так: отбрасывают содержимое лишних младших разрядов и анализируют значение первой из отброшенных цифр a_-k-1a_-k-2¼a_-m.

Если a_-k-1<5 (первая из отброшенных цифр меньше пяти), то

A@A_окр=A_усеч=0.a_-1a_-2¼a_-k.

Если же a_-k-1³5 (первая из отброшенных цифр больше четырех), то

A@Aокр= +	0.a-1a-2¼a-k	Aусеч
0.0-10-2¼1-k

(к A_усеч прибавляют единицу младшего разряда).

Максимальная абсолютная погрешность такого округления вдвое меньше и составляет половину единицы младшего числа A_окр:

DA_max=4_-k-19_-k-2¼9_-m´10^-k=5_-k-10_-k-2¼0_-m=0.5´10^-k,

На практике применяют именно этот алгоритм округления десятичных дробей. Округлим для примера число e сначала до пяти знаков после запятой, затем до двух, до одного, а потом и до целых:

2½.7½1½828½1828459045…@[email protected]@2.7@3.

Точно так округляют и большие числа. Например, число

B=428169807=4₈2₇8₆1₅6₄9₃8₂0₁7₀

округлим до двух старших цифр:

B@4300000000.

Зачастую в одном наборе данных собраны числа, существенно различающиеся по абсолютной величине. В этих случаях удобно бывает каждое число A представлять в стандартной форме, а именно, в виде произведения мантиссы M_A и масштабного множителя 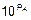(здесь P_A – порядок числа A):

A=M_A´ .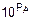

При этом 1£M_A£9, то есть целая часть мантиссы занимает один разряд и в этом разряде записан не нуль. Запишем, к примеру, числа 234507 и 0.01385462 в стандартной форме с мантиссой, округленной до двух разрядов после точки:

234507=2.34507´10⁵@2.35´10⁵,

0.01385462=1.385462´10^-2@1.39´10^-2.

Стандартная форма записи чисел удобна для выполнения операций умножения и деления. Мантисса произведения (частного) вычисляется путем умножения (деления) мантисс исходных чисел, а порядок результата вычисляют путем сложения (вычитания) их порядков. Например,

234507´0,[email protected]´10⁵´1.39´10^-2@3.27´10³.

0.01385462:234507@(1.39´10^-2):(2.35´10⁵)@0.591´10^-7.

При необходимости результат приводится к стандартной форме. Так, в последнем примере

0.591´10^-7=5.91´10^-8.

Отметим, что для выполнения операций сложения и вычитания числа в стандартной форме должны быть преобразованы к обычному виду. А результаты этих операций снова преобразуются к стандартной форме.

Натуральные и целые числа. Натуральные числа – один, два, три и т.д. используют для счета предметов и для обозначения их количества. Например, двести сорок пять студентов первого курса РАП, тридцать четвертая страница учебника по математике. В практике вычислений, как мы уже отметили, оперируют не с самими предметами в заданном количестве (студентами, страницами), а с записями соответствующих чисел (245, 24).

Над натуральными числами можно выполнять все арифметические операции. Однако эти операции неравноценны. Результаты операций сложения и умножения натуральных чисел оказываются тоже натуральными. При этом результат не зависит от порядка слагаемых и сомножителей. Что касается операции вычитания натуральных чисел, то здесь ситуация такая. Если уменьшаемое больше вычитаемого, то разность – число натуральное: 5-3=2. Если же уменьшаемое меньше вычитаемого, то разность уже не натуральное число: 3-5=-2. Это число отрицательное. Числа 2 и -2 называют противоположными. Очевидно, что каждое натуральное число имеет противоположное отрицательное. Число, противоположное отрицательному, называют положительным. Запись положительного числа начинают знаком плюс +. Запись отрицательного числа начинают знаком минус -. Между противоположными числами +1 и -1 стоит число 0 (нуль), которое противоположного не имеет. Нуль предметов означает, что таких предметов нет (например, количество неудовлетворительных оценок на экзамене по математике). Число нуль относят к положительным, хотя знаком + обычно не снабжают. Остальные положительные числа тоже чаще всего записывают без знака +.

Отрицательные и положительные числа в совокупности образуют множество целых чисел. На числовой прямой целые числа представлены точками, которые разделены отрезками длиною в 1. Между этими точками целых чисел нет.

На множестве целых чисел устраняется недостаток операции вычитания натуральных чисел. Результатом вычитания целых чисел будет целое число. А вот операция деления целых чисел не всегда дает целое число.

Таким образом, класс натуральных чисел замкнут только относительно операций сложения и умножения, класс целых чисел замкнут относительно операций сложения, вычитания и умножения.

Опишем еще одну операцию над целыми числами.

Пусть A и M – два произвольных целых положительных числа, причем M>1. Тогда A можно представить такой суммой:

A=M´D+(A)_{mod M},

где (A)_{mod M} – остаток от деления A на M нацело (то есть D – тоже целое, оно показывает, сколько раз M укладывается в A),

0£(A)_{mod M}£M-1.

Говорят, что найти (A)_{mod M} значит представить число A по модулю M:

(A)_{mod M}=A-M´D.

Например, M={20,31}, A={120, 155, 13}.

(120)_{mod 31}=27, (155) _{mod 31}=0, (13)_{mod 31}=13,

(120)_{mod 20}=0, (155) _{mod 20}=15, (13)_{mod 20}=13.

Ради интереса отметим, что (A)_{mod 10} есть младшая цифра в записи A. В самом деле, остаток от деления любого A на 10 всегда меньше десяти, а значит, равен тому элементу множества {0,1,2,3,4,5,6,7,8,9}, который и стоит в младшем разряде А.

При исследовании того или иного социального явления (например, преступности) важную роль играют сбор и обработка статистических данных, которые несут информацию об этом явлении. Цель обработки данных состоит в получении обобщающих характеристик изучаемого явления. В юридической статистике разработана целая система обобщающих характеристик. Здесь мы остановимся только на таких показателях, которые представлены абсолютными и относительными величинами.

Дата добавления: 2014-11-18