
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Элементы статистической обработки данных 7 страница
|
|
|
|
Теперь легко (практически в уме) вычислим
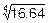 @
@ 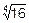 ´
´ 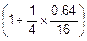 =2´1.01=2.02.
=2´1.01=2.02.
Вопросы и задачи для самоконтроля
1. Дать определение производной и пояснить ее геометрический смысл.
2. Найти производные функций:
а) y= 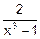 , б) y=
, б) y= 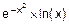 , в) y=
, в) y=  ,
,
г) y=log2(x2), д) y=arccos(x), е) y=arctg(x).
3. Пояснить, как используется производная для исследования функций.
4. Исследовать функцию y=x3-3´x2-9´x+14 и построить ее график на отрезке [-2,+4].
5. Дать определение дифференциала функции и пояснить его геометрический смысл.
6. Записать дифференциалы функций:
а) y=(x+1)4, б) y=sin2(x), в) y=  .
.
7. Пояснить, как используется дифференциал функции в приближенных вычислениях. Формула для вычисления погрешности функции из-за погрешности аргумента. Формула для вычисления нового значения функции по ее старому значению и приращению аргумента.
8. Вычислить приближенные значения величин:
а) 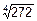 , б) e1.05, в) ln(e+0.272), г) sin(240).
, б) e1.05, в) ln(e+0.272), г) sin(240).
9. Выполнить ДКЗ: Тест 5.ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ.
Глава 6. ОСНОВЫ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
6.1. Определенный интеграл
К понятию определенного интеграла привели задачи вычисления обобщенных характеристик сложных процессов (скажем, таких как динамика преступности, безработицы и др.).

Пусть некоторый процесс y на отрезке [a,b] описывается функцией f(x). Обобщенной характеристикой этого процесса будет величина yср – среднее значение для yÎ[f(a),f(b)]:
yср=  .
.
Здесь F – площадь криволинейной трапеции aABb (рис.6.1). Как видим, yср – суть высота прямоугольника aCDb, площадь которого тоже будет равна F.
Для определения yср нужно вычислить площадь F, которая ограничена кривой f(x) на отрезке [a,b]. Решение этой задачи описывается такой конструкцией:
F= 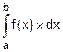 .
.
Правая часть этой записи читается так: определенный интеграл от a до b от f(x) по dx. Здесь:
f(x) – подынтегральная функция,
a – нижний предел интегрирования,
b – верхний предел интегрирования.
Итак, геометрический смысл определенного интеграла:
определенный интеграл от a до b от f(x) по dx – площадь, ограниченная кривой f(x) на отрезке [a,b].
Обычно для вычисления определенного интеграла пользуются формулой Ньютона-Лейбница:
F=FNL= 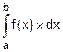 =F(x)
=F(x) 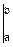 =F(b)-F(a), (6.1)
=F(b)-F(a), (6.1)
где FNL – значение определенного интеграла F, полученное по формуле Ньютона-Лейбница,
F(x) –первообразная для подынтегральной функции f(x).
Функция F(x) называется первообразной для функции f(x), если f(x) получена как результат дифференцирования F(x):
f(x)=F’(x).
Например, для f(x)=3´x2 первообразной будет F(x)=x3. В самом деле, (x3)’=3´x2. Однако легко заметить, что и (x3-1000)’=3´x2, и (x3+0.001)’=3´x2, и вообще (x3+C)’=3´x2. Поэтому, если F(x) – первообразная для f(x), а C – любая константа, то и функция F(x)+C также будет первообразной для f(x), то есть
f(x)=(F(x)+C)’. (6.2)
Вычисление первообразной F(x) для f(x) называют интегрированием функции f(x) и задают такой записью:
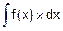 =F(x).
=F(x).
Левая часть этой формулы читается так: неопределенный интеграл от f(x) по dx. Говорят, что для отыскания первообразной F(x) для f(x) нужно взять интеграл от функции f(x) или проинтегрировать функцию f(x).
Отметим, что Ньютон и Лейбниц практически в одно и то же время изобрели дифференциальное и интегральное исчисления. Однако юрист Лейбниц в отличие от физика Ньютона понимал важность эффективной математической символики, благодаря которой «поразительным образом сокращается работа мысли». Именно Лейбниц применил символ d для дифференциала и символ 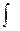 для интеграла.
для интеграла.
Формулой (6.1) кодируют такую двухэтапную процедуру вычисления определенного интеграла.
Этап 1. Вычисляют неопределенный интеграл 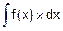 и находят выражение F(x) для первообразной.
и находят выражение F(x) для первообразной.
Этап 2. В полученную формулу F(x) подставляют сначала x=b и находят число F(b), потом в формулу F(x) подставляют x=a и находят число F(a), а затем путем вычитания F(a) из F(b) находят искомое значение F=FNL.
В этой процедуре наибольшую сложность представляет этап 1. Поэтому остановимся подробно на методах вычисления неопределенных интегралов.
Отметим для начала, что в математике (строгости ради) результат вычисления первообразной записывают с учетом факта (6.2):
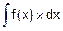 =F(x)+C
=F(x)+C
и константу C называют произвольной постоянной интегрирования. Подставим в формулу Ньютона-Лейбница вместо F(x) сумму F(x)+C:
(F(x)+C) 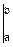 =(F(b)+C)-(F(a)+C)=F(b)-F(a)=F(x)
=(F(b)+C)-(F(a)+C)=F(b)-F(a)=F(x) 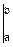 .
.
Как видим, для наших целей отмеченная строгость не нужна, и результат вычисления неопределенного интеграла  для использования его в формуле Ньютона-Лейбница достаточно представить только формулой F(x) (без слагаемого C).
для использования его в формуле Ньютона-Лейбница достаточно представить только формулой F(x) (без слагаемого C).
При вычислении первообразной F(x) используют свойства интегралов, таблицы интегралов от типовых функций, те или иные приемы интегрирования.
Свойства интегралов. Сначала свойства неопределенных интегралов.
1. Неопределенный интеграл всегда берется от дифференциала искомой функции F(x):
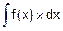 =
= 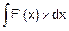 =
=  =F(x).
=F(x).
2. Константу можно выносить за знак интеграла.
Пусть A=const. Тогда
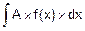 =
= 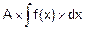 .
.
3. Интеграл от суммы функций равен сумме интегралов от функций-слагаемых:
 =
= 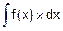 +
+  .
.
Свойствами 2 и 3 обладают и определенные интегралы. Укажем еще два свойства определенных интегралов.
4. Если отрезок интегрирования [a,b] разбить на части, то интеграл по целому отрезку равен сумме интегралов по этим частным отрезкам:
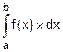 =
=  +
+  .
.
Иногда слагаемые в правой части этого равенства вычислить проще, чем его левую часть.
5. Перестановка пределов интегрирования равносильна изменению знака определенного интеграла:
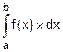 =
=  .
.
Действительно,
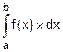 =F(b)-F(a)=-(F(a)-F(b))=
=F(b)-F(a)=-(F(a)-F(b))=  .
.
Значит, и
F(x) 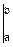 =-F(x)
=-F(x) 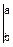 .
.
Таблица интегралов. В математике разработаны таблицы интегралов от тысяч функций. Мы же ограничимся таблицей интегралов от нескольких типовых функций (табл. 6.1).
| Таблица 6.1 | |
| a) | 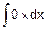 =0 =0
|
| b) |  p¹-1(!)
p¹-1(!)
|
| с) | при p=-1
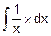 =ln(x), x>0! =ln(x), x>0!
|
| d) | 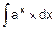 = = 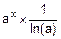
|
| e) | 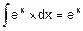
|
| f) | 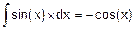
|
| g) | 
|
 Пример. Докажем верность формул в строках c) и d) табл. 6.1:
Пример. Докажем верность формул в строках c) и d) табл. 6.1:
c)  =
=
= 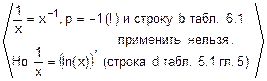 =
=
=  =
=  =
=
= á свойство 1 интегралов ñ =ln(x).
d) 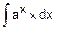 =
=
= 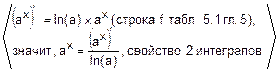 =
=
= 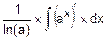 =
= 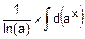 =
=
= á свойство 1 интегралов ñ = 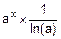 .
.
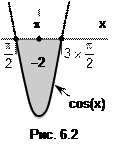
 Еще пример. Вычислим (рис.6.2) площадь, ограниченную кривой f(x)=cos(x) на отрезке
Еще пример. Вычислим (рис.6.2) площадь, ограниченную кривой f(x)=cos(x) на отрезке  .
.
F= 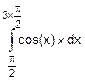 .
.
Этап 1.
F(x)=  .
.
Этап 2.
F=FNL=sin(x)  =
=  =-2.
=-2.
Этот пример иллюстрирует важную особенность определенного интеграла. В записи 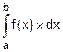 объекты x, f(x), dx, a, b – величины алгебраические, разность F(b)-F(a) в формуле Ньютона-Лейбница тоже величина алгебраическая. Значит, и FNL – алгебраическая величина (и, как в нашем примере, может принимать отрицательное значение).
объекты x, f(x), dx, a, b – величины алгебраические, разность F(b)-F(a) в формуле Ньютона-Лейбница тоже величина алгебраическая. Значит, и FNL – алгебраическая величина (и, как в нашем примере, может принимать отрицательное значение).
В математике разработано огромное количество приемов интегрирования, которые применяются на первом этапе вычисления определенного интеграла и позволяют любой неопределенный интеграл преобразовать к табличному. Мы же опишем только два классических приема интегрирования.
Замена переменной. Этот прием применяется тогда, когда заданный интеграл имеет такой вид:
F=  ,
,
то есть под знаком интеграла стоит произведение сложной функции f(j(x)) на дифференциал вложенной функции j’(x)´dx.
На первом этапе вычисления определенного интеграла F выполняют замену t=j(x). Тогда dt=dj(x)=j’(x)´dx и
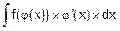 =
= 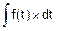 =F(t).
=F(t).
Для того чтобы формулу F(t) можно было бы использовать на втором этапе вычисления определенного интеграла, необходимо и пределы a и b по переменной x заменить пределами at и bt по переменной t: at=j(a), bt=j(b). Тогда
F=FNL=F(t)  =F(bt)-F(at).
=F(bt)-F(at).
 Пример. Вычислим
Пример. Вычислим
F= 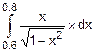 .
.
Этап 1.
F(x)= 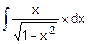 =
=
= 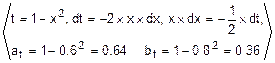 =
=
= 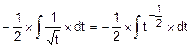 =
=
= 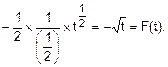
Этап 2.
F=FNL= 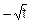
 = á свойство 5 интегралов ñ =
= á свойство 5 интегралов ñ =
= 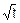
 =
= 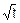
 =
=  =0.2.
=0.2.
Интегрирование по частям. Напомним формулу вычисления производной от произведения функций:
(u(x)´v(x))’=u’(x)´v(x)+ u(x)´v’(x).
Ясно, что первообразная для правой части этого равенства равна первообразной для его левой части:
u(x)´v(x)=  .
.
Перепишем это равенство так:
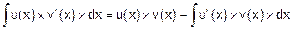 .
.
В результате получили формулу интегрирования по частям. Ее можно записать более компактно, положив u(x)=u, v(x)=v,  и
и  :
:
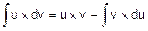 .
.
Итак, если под знаком интеграла стоит произведение одной функции u на дифференциал dv от другой функции v, то, применив формулу интегрирования по частям, получим интеграл 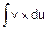 , который может оказаться табличным.
, который может оказаться табличным.
 Пример. Вычислим
Пример. Вычислим
F=  .
.
Этап 1.
F(x)= 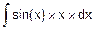 =
=
= 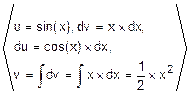 =
=
= 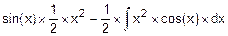 .
.
Второй интеграл 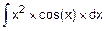 оказался не табличным и сложнее исходного
оказался не табличным и сложнее исходного 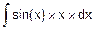 . Значит, наш выбор u и dv оказался неудачным. Попробуем другой вариант назначения u и dv.
. Значит, наш выбор u и dv оказался неудачным. Попробуем другой вариант назначения u и dv.
F(x)= 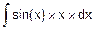 =
=
=  =
=
= 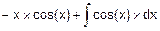 =
= 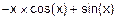 .
.
Этап 2.
F=FNL=(-x´cos(x)+sin(x))  =
=
=(-p´cos(p)+sin(p))-(-0´cos(0)+sin(0p))=p.
Чтобы применить прием интегрирования по частям, нужно уметь разбить подынтегральное выражение на два множителя, а именно, на u и на dv. Никаких общих правил для этого нет, кроме следующих:
§ dx должен быть всегда частью dv,
§ нужно уметь брать интеграл от dv,
§ когда интегрируемое выражение есть произведение двух функций, более сложную из них нужно рассматривать как часть дифференциала dv.
Во многих случаях один или оба предела интегрирования в определенном интеграле бесконечны. Интегралы с такими пределами относятся к несобственным интегралам. Операции взятия предела и интегрирования линейны: предел (интеграл) суммы равен сумме пределов (интегралов), а константу можно выносить за знак предела (интеграла). Поэтому определенный интеграл с бесконечным верхним пределом вычисляют так:
 .
.
 Пример. Вычислить несобственный интеграл
Пример. Вычислить несобственный интеграл
F=  .
.
Этап 1.
F(x)= 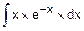 =
=
= 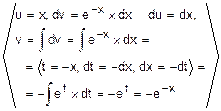 =
=
=  =
= 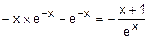 .
.
Этап 2.
F=FNL=  =
= 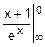 =
=
=1-  =1-
=1- 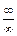 !
!
Как видим, прямая подстановка b=¥ в выражение 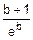 под знаком предела дает неопределенность вида
под знаком предела дает неопределенность вида 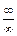 . Рассмотрим эту ситуацию подробнее.
. Рассмотрим эту ситуацию подробнее.
Если 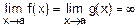 , то вычисление
, то вычисление  путем прямой подстановки приводит к неопределенности вида
путем прямой подстановки приводит к неопределенности вида 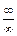 . Раскрывают эту неопределенность по правилу Лопиталя:
. Раскрывают эту неопределенность по правилу Лопиталя:
 =
= 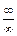 !=
!= 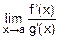 =
=  .
.
Точно так записывается правило Лопиталя и для раскрытия неопределенности вида 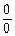 , когда
, когда
 =
= 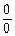 !=
!= 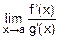 =
=  .
.
Таким образом, правило Лопиталя состоит в том, что отношение функций  под знаком предела заменяется отношением их производных
под знаком предела заменяется отношением их производных 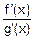 , и уже в это новое отношение делают прямую подстановку.
, и уже в это новое отношение делают прямую подстановку.
Значит, в нашем случае
 =
= 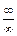 !=
!= 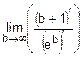 =
= 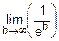 =
=  =0.
=0.
Итак,
F=FNL=  =
=  =
=  =
= 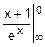 =
=
=1-  =1-
=1- 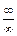 !=1-
!=1- 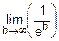 =1-0=1.
=1-0=1.
Аналогично вычисляют определенный интеграл с бесконечным нижним пределом:
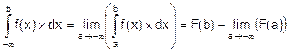 ,
,
с бесконечными верхним и нижним пределами интегрирования:
 .
.
6.2. Машинные алгоритмы
вычисления определенных интегралов
Нередко бывает так, что воспользоваться формулой Ньютона-Лейбница для вычисления определенного интеграла не удается. Во-первых, получение аналитического выражения для F(x), когда оно существует, базируется на многочисленных приемах и ухищрениях. Замена переменной и интегрирование по частям – далеко не самые хитроумные из этих приемов. Освоить эти приемы и ухищрения – задача не из легких. Да и распознать по формуле f(x), какой из приемов для нее походит, тоже своего рода искусство. Поэтому часто усилия на получение аналитического выражения для F(x) оказываются чрезмерной платой за искомое число F. Во-вторых, далеко не каждая аналитически заданная функция f(x) имеет первообразную F(x) в форме аналитического выражения. Например, нет первообразной такой для функции f(x)=  . И, наконец, когда f(x) задана таблицей, взять интеграл аналитически от такой функции вообще невозможно. Поэтому для вычисления определенных интегралов применяют методы численного интегрирования. Эти методы универсальны и пригодны для любых f(x), (не только тогда, когда для f(x) нет F(x), но и тогда, когда можно было бы воспользоваться формулой Ньютона-Лейбница). На компьютерах методы численного интегрирования реализованы в виде стандартных программ.
. И, наконец, когда f(x) задана таблицей, взять интеграл аналитически от такой функции вообще невозможно. Поэтому для вычисления определенных интегралов применяют методы численного интегрирования. Эти методы универсальны и пригодны для любых f(x), (не только тогда, когда для f(x) нет F(x), но и тогда, когда можно было бы воспользоваться формулой Ньютона-Лейбница). На компьютерах методы численного интегрирования реализованы в виде стандартных программ.
Рассмотрим один из самых простых, но достаточно эффективных методов численного интегрирования – формулу трапеций.
Для численного интегрирования любую подынтегральную функцию f(x) на отрезке [a,b] задают таблицей {xti,yti}, у которой сетка a=xt0,xt1,...,xtk,xtk+1,...,xtn=b имеет достаточно малый шаг h=  , а ytk=f(xtk) – отсчеты табличной функции (k=
, а ytk=f(xtk) – отсчеты табличной функции (k= 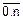 ). К этой таблице применяют линейную аппроксимацию, а именно, на каждом интервале таблицы [xtk,xtk+1] длиною в h функцию f(x) заменяют прямой jk(x). Так вместо кривой f(x) получают ломаную линию j(x)={j0(x), j1(x),¼, jk(x), jk+1(x),¼, jn-1(x)} (рис.6.3).
). К этой таблице применяют линейную аппроксимацию, а именно, на каждом интервале таблицы [xtk,xtk+1] длиною в h функцию f(x) заменяют прямой jk(x). Так вместо кривой f(x) получают ломаную линию j(x)={j0(x), j1(x),¼, jk(x), jk+1(x),¼, jn-1(x)} (рис.6.3).

Далее, вместо того, чтобы вычислять площадь, ограниченную кривой f(x), вычисляют площадь, ограниченную ломаной j(x). Для этого находят площади трапеции s0, s1,¼, sk, sk+1,¼, sn-1:
sk=  , k=
, k=  .
.
А потом все эти площади суммируют:
Fh=s0+s1+¼+sk+sk+1+¼+sn-2+sn-1=
=  =
=
= 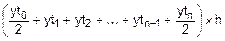 .
.
Результатом суммирования и будет формула трапеций:
Fh=  . (6.2)
. (6.2)
Здесь Fh – значение определенного интеграла от функции f(x) по формуле трапеций на шаге h.
Достоинство формулы трапеций состоит в том, что процедура вычисления определенного интеграла не зависит от вида подынтегральной функции f(x), и сводится к простому суммированию отсчетов yt0, yt1,¼, ytn табличной функции {xti,yti} с последующим умножением этой суммы на шаг таблицы h.
Если точным значением искомого интеграла будет величина F, то погрешность формулы трапеций на шаге h составит
Rh=F-Fh=C´h2, (6.3)
где C@const. Говорят, что формула трапеций имеет второй порядок точности (потому, что ее погрешность Rh пропорциональна h2). Повышают точность вычисления интеграла по формуле (6.2) путем уменьшения шага таблицы h (или, что то же самое, увеличением объема таблицы n). Второй порядок точности формулы трапеций означает, что уменьшение h вдвое снижает погрешность интегрирования в четыре раза. Однако пользоваться формулой (6.3) для оценки точности интегрирования неудобно. Дело в том, что здесь величина C не определена. Позже мы найдем более удобный способ оценивать погрешность численного интегрирования по формуле трапеций.
Допустим, что для заданной табличной функции {xti,yti} по формуле (6.2) получены: значение интеграла F2h на шаге 2´h и значение Fh на шаге h. Тогда, пользуясь формулой (6.3), можно составить следующую систему уравнений:
 (6.4)
(6.4)
Исключив из этих уравнений неизвестное C, получим формулу Рунге-Ромберга для вычисления определенного интеграла:
F=Fh+ 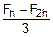 .
.
Второе слагаемое в этой формуле
PR= 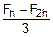 (6.5)
(6.5)
называют поправкой Рунге. Пользуясь этим обозначением, перепишем формулу Рунге-Ромберга:
F=FRR=Fh+PR. (6.6)
Здесь FRR – значение определенного интеграла, вычисленное методом Рунге-Ромберга по формуле трапеций.
Формула (6.6) имеет четвертый порядок точности (уменьшение шага интегрирования вдвое уменьшает погрешность интегрирования в 24=16 раз). Достигается это за счет грамотного использования избыточной информации – результата интегрирования F2h на шаге 2´h (для вычисления поправки Рунге PR). Отметим интересный факт: когда f(x) – полином степени не выше третьей, формула Рунге-Ромберга дает точное значение определенного интеграла, хотя F2h и Fh вычисляются по формуле трапеций с погрешностями.
Поправку Рунге можно использовать для оценки текущей точности интегрирования по формуле трапеций. В самом деле, вычтем первое уравнение из второго в системе (6.4):
Fh-F2h=C´h2´3, C´h2= 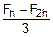 .
.
|
|
|
|
|
Дата добавления: 2014-11-18; Просмотров: 430; Нарушение авторских прав?; Мы поможем в написании вашей работы!