Элементы статистической обработки данных 12 страница

2. Величина H(X) зависит от вероятностей p(x_i) и достигает максимального значения тогда, когда события x_i равновероятны:

p(x₁)=p(x₂)=¼=p(x_N)=p.

И эти вероятности отвечают условию (8.19): N´p=1. Поэтому

p= .

В этом случае

H(X)= 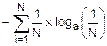=áN одинаковых слагаемыхñ=

=-N´ 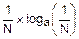=log_a(N).

Формулу

H(X)=log_a(N) (8.21)

для энтропии множества равновероятных событий вывел в 1928 г. американский инженер Р. Хартли. Это была первая попытка количественной оценки энтропии.

Основание a логарифма в формулах (8.20) и (8.21) определяет единицу измерения энтропии. Действительно,

H(X)=log_a(N)=1

тогда, когда a=N. В настоящее время общепринято использование в формулах (8.20) и (8.21) значения a=N=2, что хорошо согласуется с математической логикой и двоичным кодированием информации. Единицей измерения энтропии, а значит, и информации при a=2 является бит (англ. bit от сжатия слов binary digit). История науки знает случаи использования и таких единиц, как нит (a=e) и дит (a=10). Один бит равен 1.44 нит (log₂(e)) или 3.32 дит (log₂(10)).

Пример. Пусть некто первый случайным образом загадывает целое число из диапазона X=[0,15]. При этом он никогда не загадывает круглые числа, а предпочтение отдает простым числам (табл. 8.5). Вычислим энтропию такого множества случайных событий. В этом случае необходимо применить меру Шеннона (8.20) для N=16. Вычисляем сначала log₂(p(x_i)), потом произведения p(x_i)´log₂(p(x_i)). Далее суммируем эти произведения, знак суммы инвертируем и получаем

Таблица 8.5
i	xi	p(xi)
		0.0000
		0.1250
		0.1250
		0.1250
		0.0179
		0.1250
		0.0179
		0.1250
		0.0179
		0.0179
		0.0000
		0.1250
		0.0179
		0.1250
		0.0179
		0.0179

H(X)=3.351 бита.

Изменим условие задачи так. Некто первый не отдает предпочтения ни одному из этих чисел. Вычислим энтропию множества X.

В данном случае, как и ранее, N=16, но все исходы загадывания равновероятны: p= 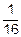, и для вычисления энтропии воспользуемся мерой Хартли (8.21):

H(X)=log₂(16)=4 бита.

Как видим, энтропия множества неравновероятных событий меньше энтропии множества равновероятных событий.

Пример. Пусть загадано число 13, и некто второй должен определить загаданное число. Покажем, что для этого достаточно задать первому четыре вопроса (табл. 8.6). Как видим, после ответа на каждый вопрос диапазон чисел, среди которых и загаданное, уменьшается вдвое, и после четвертого вопроса остается одно загаданное число.

Вычислим, какое количество информации получено после ответа на первый вопрос. До ответа на первый вопрос имеем

H_ДО=H(X)=4 бита.

Ответ на первый вопрос показал, что задуманное число находится во второй половине диапазона [0,15]. Значит, вероятности для чисел из первой его половины равны нулю, а вероятности для чисел из второй половины удвоились и составляют 0.1250 (сумма вероятностей для этих чисел отвечает условию (8.19)). Энтропию такого множества неравновероятных событий следует вычислять по формуле Шеннона (8.20). Учтем, что в сумме (8.20) первые восемь слагаемых равны нулю, потому что у них p(x_i)=0 (см. табл. 8.6). Поэтому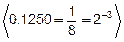

Таблица 8.6
Вопрос	-	>7?	>11?	>13?	>12?
Ответ	-	Да.	Да.	Нет.	Да.
i	xi	p(xi)	p(xi)	p(xi)	p(xi)	p(xi)
		0.0625
		0.0625
		0.0625
		0.0625
		0.0625
		0.0625
		0.0625
		0.0625
		0.0625	0.1250
		0.0625	0.1250
		0.0625	0.1250
		0.0625	0.1250
		0.0625	0.1250	0.2500	0.5000
		0.0625	0.1250	0.2500	0.5000	1.0000
		0.0625	0.1250	0.2500
		0.0625	0.1250	0.2500
H(X)
I(X)

H_ПО= =

=áвосемь одинаковых слагаемыхñ=

= =3 бита.

Значит, количество информации, полученное после ответа на первый вопрос, равно

I1(X)=H_ДО-H_ПО=4-3=1 бит.

Перед ответом на второй вопрос имеем H_ДО=3 бита. Ответ на второй вопрос показал, что задуманное число находится в диапазоне [12,15], и вероятности для каждого из чисел этого диапазона равны 0.2500= 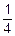=2^-2. Тогда

H_ПО= 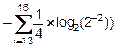=2 бита.

I2(X)=H_ДО-H_ПО+I1(X)=3-2+1=2 бита.

Перед ответом на третий вопрос имеем H_ДО=2 бита. Ответ на третий вопрос показал, что задуманное число находится в диапазоне [13,14], и вероятности для каждого из чисел этого диапазона равны 0.5000= 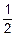=2^-1. Тогда

H_ПО= =1 бит.

I3(X)=H_ДО-H_ПО+I2(X)=2-1+2=3 бита.

Перед ответом на четвертый вопрос имеем H_ДО=1 бита. После ответа на четвертый вопрос остается только искомое число 13 с вероятностью, равной 1, то есть H_ПО=0.

I4(X)=H_ДО-H_ПО+I3(X)=1-0+3=4 бита.

Значит, полная информация, полученная в ответах на четыре вопроса, составит

I(X)=I4(X)=H(X)=4 бита.

Положим, что в опыте одновременно участвуют и множество X с энтропией H(X), и множество Y с энтропией H(Y). Результатом того или иного испытания может быть и исход x_i из X, и исход y_j из Y, то есть событие x_i´y_j (i= 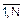, j= 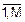). Говорят, что в таком опыте оперируют с множеством X´Y. Если события x_i и y_j независимы, то

p(x_i´y_j)=p(x_i)´p(y_j),

а энтропия H(X´Y) множества X´Y, когда x_i и y_j независимы, равна

H(X´Y)=H(X)+H(Y). (8.22)

Формула (8.22) справедлива для любого числа k участвующих в опыте множеств. А если все они еще и одинаковы, то есть оперируют с множеством X^k, то

H(X^k)=k´H(X).

Пример. Из 32 символов множества X составляют сообщения из трех символов. Какое количество информации несет такое сообщение?

Здесь множество случайных событий X мощностью N=32. Ни один из символов не имеет преимуществ перед другими, то есть все они равновероятны в одной выборке. Значит, энтропия множества X при выборе одного символа вычисляется по формуле Хартли:

H(X)=log₂(N)=log₂(32)=5 битов.

При выборе трех символов множество X используется k=3 раза, то есть в сообщениях из трех символов оперируют с множеством X³, а элементом этого множества является любое трехсимвольное сообщение. Тогда энтропия множества X³ равна

H(X³)=3´H(X)=15 битов.

До составления того или иного сообщения неопределенность в исходе этого опыта есть

H_ДО=H(X³))=15 битов.

После формирования конкретного сообщения неопределенность в исходе опыта отсутствует. А это означает, что

H_ПО=0.

Значит,

I(X)=H_ДО-H_ПО=15 битов.

Отметим, что общее количество k-символьных сообщений, которые можно составить из N символов равно N^k, потому что в каждую из k позиций для сообщения можно поместить любой из N символов. В нашем примере из 32 символов можно составить 32³=2¹⁵=32768 трехсимвольных сообщений.

Положим теперь, что события x_i и y_j зависимы. Тогда

p(x_i´y_j)=p(x_i)´p(y_jïx_i)=p(y_j)´p(x_iïy_j),

где

p(y_jïx_i) – условная вероятность события y_j, а именно, вероятность события y_j, вычисленная при том условии что x_i произошло,

p(x_iïy_j)– условная вероятность события x_i, а именно, вероятность события x_i, вычисленная при том условии что y_j произошло.

Энтропия H(X´Y) множества X´Y, когда x_i и y_j зависимы, равна

H(X´Y)=H(Y)+H(XïY)=H(X)+H(YïX)). (8.22)

Здесь

H(X½Y) – условная энтропия множества X. Она характеризует среднюю неопределенность множества X, которая остается после наступления того или иного события из множества Y,

H(Y½X) – условная энтропия множества Y. Она характеризует среднюю неопределенность множества Y, которая остается после наступления того или иного события из множества X.

С условными энтропиями оперируют в системах коммутации.

На вход системы поступает сообщение x_i из входного ИМ X. На выходе системы коммутации появляется сообщение y_j из выходного ИМ Y. Получив сообщение y_j, нельзя утверждать, что оно точно совпадает с сообщением x_i поскольку система коммутации подвержена воздействию помех. Таким образом, выходной ИМ Y отображает входной ИМ X со средней неопределенностью H(XïY). До выполнения опыта со входным ИМ X неопределенность его исхода характеризуется энтропией

H_ДО=H(X).

После опыта о его результате судят по выходному ИМ Y с неопределенностью

H_ПО=H(X½Y).

Количество информации I(X,Y) о событиях входного ИМ X, которое получают в событиях выходного ИМ Y, вычисляют так:

I(X,Y)=H(X)-H(X½Y). (8.23)

Точно так, имея сообщение x_i, нельзя утверждать, что оно совпадает с сообщением y_j. То есть входной ИМ X отображает выходной ИМ Y со средней неопределенностью H(YïX). До выполнения опыта со выходным ИМ Y неопределенность его исхода характеризуется энтропией

H_ДО=H(Y).

После опыта о его результате судят по входному ИМ X с неопределенностью

H_ПО=H(Y½X).

Количество информации I(X,Y) о событиях выходного ИМ Y, которое получают в событиях входного ИМ X, вычисляют так:

I(X,Y)=H(Y)-H(Y½X). (8.24)

Рис. 8.13, который называют диаграммой Венна, наглядно иллюстрирует соотношения между описанными энтропийно-информационными понятиями системы коммутации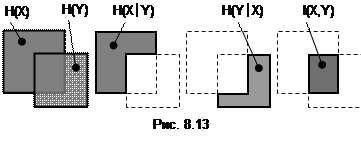
.

Пример. Рассмотрим простейшую систему коммуникации, в которой входной информационный массив X задан всего двумя символами x₁=0, x₂=1, а выходной – тоже всего двумя символами y₁=0, y₂=1. Положим, что вероятность ошибки при приеме символа равна p, а вероятность безошибочного приема символа равна 1-p.

На рис. 8.14 схематически показана такая система коммуникации. Стрелки показывают, в какие символы множества Y и с какой вероятностью переходит каждый из символов множества X. В теории информации такая система коммуникации называется двоичным симметричным каналом связи.

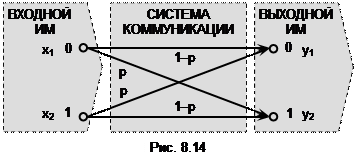
Вычислять количество информации I(X,Y) будем по формуле (В.7), в которой энтропия H(Y) имеет максимально возможное значение H(Y)=1, а условная энтропия H(Y½X) определяется соотношением (дается без вывода)

H(Y½X)=-(p´log₂(p)+(1-p)´log₂(1-p)). (8.25)

Тогда

I(X,Y)=1-H(Y½X)= (8.26)

=1+(p´log₂(p)+(1-p)´log₂(1-p)).

На рис. 8.15 показаны графики H(Y½X) и I(X,Y), построенные по формулам (8.25) и (8.26). Как видим, с увеличением p от 0 до 0.5 условная энтропия H(Y½X) возрастает, а количество информации о массиве X в массиве Y падает.

При p=0.5 оказывается, что H(Y½X)=1, а I(X,Y)=0. Объясняется это тем, что при p=0.5 теряется зависимость между символами массивов X и Y. Когда передается символ x₁=0, на выходе с равной вероятностью принимается или символ y₁=0, или символ y₂=1. То же самое имеет место и при передаче символа x₂=1. Значит, при p=0.5 неопределенность выходного массива Y при известном входном массиве X максимальна, и элементы массива Y не содержат никакой информации о символах массива X.

С увеличением p от 0.5 до 1 условная энтропия H(Y½X) падает, а количество информации I(X,Y) растет. Дело в том, что при высокой вероятности ошибки p передача символа x₁=0 чаще всего вызывает появление на выходе символа y₂=1, а при передаче x₂=1 на выходе чаще всего будет y₁=0. Если при p>0.5 выполнять инверсию символов на выходе (замену нуля на единицу, а единицы на нуль), то вероятность искажения результата инверсии будет равна 1-p<0.5.

Вопросы и задачи для самоконтроля

1. Сформулируйте понятие случайной величины дискретной и непрерывной.

2. Определить понятие «закон распределения СВ».

3. Определить понятие «ряд распределения» дискретной случайной величины.

4. Определить понятие «функция распределения». Перечислить ее свойства.

5. Определить понятие «плотность распределения». Перечислить ее свойства.

6. Дать определение каждой из числовых характеристик случайной величины дискретной и непрерывной. Что в поведении случайной величины характеризуют ее математическое ожидание и дисперсия?

7. Бросают два игральных кубика. Найти закон распределения и числовые характеристики для суммы выпавших очков.

8. Среди денежных банкнот 20% фальшивых. Наугад берут 3 купюры. Построить ряд распределения и найти числовые характеристики для случайной величины – возможного количества фальшивых купюр в этой выборке.

Таблица 8.7
X
p	0.2	0.3	0.4	0.1

9. СВ X задана рядом распределения (табл. 8.7).

Найти математическое ожидание, дисперсию и СКО этой случайной величины.

10. Плотность распределения случайной величины X задана формулой:

f(x)=

а) Записать для СВ X функцию распределения F(x).

б) Найти ее числовые характеристики m_x, D_x и s_x.

в) Построить графики f(x) и F(x), отобразить на них значения m_x и s_x.

г) Вычислить вероятность попадания значений X в интервал ]m_x-s_x, m_x+s_x[.

11. Плотность распределения случайной величины V задана рис. 8.16. Величины a и b известны.

а) Вычислить значение величины c.

б) Записать аналитические выражения для f(v) и F(v).

в) Найти числовые характеристики для СВ V: m_v, D_v, s_v.

г) Вычислить вероятность попадания значений X в интервал ]m_v-s_v, m_v+s_v[.

12. Выполнить ДКЗ: Тест 8. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ.

13. Раскрыть содержание понятий информационные технологии и структуру основных информационных процессов.

14. Изложить толкование термина информация в юриспруденции.

15. Охарактеризовать формы представления информации в юриспруденции.

16. Пояснить причину вероятностного характера процессов в системах коммуникации, смысл терминов энтропия и количество информации.

17. Раскрыть содержание меры энтропии по Шеннону и связь этой меры с мерой энтропии по Хартли. Единицы измерения энтропии.

18. В одной урне содержится 10 белых, 20 красных, 30 синих и 40 зеленых шаров, а во второй по 25 шаров каждого из названных цветов. Из каждой урны наугад вынимают по одному шару. Какое количество информации несет сообщение о цвете вынутого шара из каждой урны?

19. Какое минимальное количество двоичных символов потребуется для того, чтобы закодировать символы шестнадцатеричной системы счисления?

20. Энтропия в опытах с несколькими массивами независимых СВ.

21. Сколько четырехсимвольных комбинаций можно составить из символов шестнадцатеричной системы счисления?

22. С помощью диаграммы Венна пояснить смысл понятий:

P условные энтропии H(X½Y) и H(Y½X) в опытах с двумя массивами зависимых случайных величин.

P количество информации I(X½Y) о событиях входного ИМ, которое получают в событиях выходного ИМ.

P количество информации I(Y½X)о событиях выходного ИМ, которое получают в событиях входного ИМ.

Неправомерный доступ к охраняемой законом компьютерной информации, если это деяние повлекло уничтожение, блокирование, модификацию либо копирование информации, –

наказывается штрафом в размере до двухсот тысяч рублей или в размере заработной платы или иного дохода осужденного за период до восемнадцати месяцев, либо исправительными работами на срок до одного года, либо ограничением свободы на срок до двух лет, либо принудительными работами на срок до двух лет, либо лишением свободы на тот же срок.

(УК РФ, Ст.272, ч. 1)

РАЗДЕЛ IV.
ОСНОВНЫЕ СПОСОБЫ И МЕТОДЫ
ЗАЩИТЫ ИНФОРМАЦИИ

Глава 9. ОСНОВЫ КРИПТОГРАФИЧЕСКОЙ
ЗАЩИТЫ ИНФОРМАЦИИ

9.1. Принципы и основные понятия
криптографической защиты информации

Криптография – наука о защите информации от несанкционированного использования. В течение тысячелетий она применялась для запутывания посторонних относительно сообщений, которыми обменивались государственные деятели, в частности военные. Круг людей, применявших криптографию, был весьма ограничен, а методы этой науки держались в секрете. Однако в последние десятилетия, когда человечество вступило в эпоху информационного общества, криптографические методы защиты информации стали использоваться очень широко. Профессионально грамотная работа юристов в правовых автоматизированных информационных системах требует от них известного уровня подготовки и в области криптографии.

Изложение основ криптографии начнем с описания типовой ситуации, а именно, передачи секретных сообщений некоторым отправителем получателю. Отправителями сообщений и их получателями могут быть физические лица, организации, технические системы. Из методических соображений удобно абстрактных участников обмена сообщениями отождествить с героями фильма «Семнадцать мгновений весны». Отправитель – это Юстас, а получатель – Алекс.

Сообщения передаются по открытой системе коммуникации, в которой они в принципе доступны для перехвата лицами, отличными от получателя. Сегодня массово используется такая система коммуникации, как сеть Интернет. Она, наряду с несомненными достоинствами, оказывается уязвимой для несанкционированного доступа к сообщениям третьих лиц. В Интернете легко реализуется не только перехват, но и подмена сообщений (вредоносная их модификация). Таким образом, в криптографии у Юстаса и Алекса есть противник – старина Мюллер, который может перехватывать сообщения, передаваемые по открытому каналу. Он владеет методами криптоанализа, в основе которых лежит формально-логический аппарат для снятия секретности с перехваченных сообщений. В его распоряжении имеются самые мощные из современных вычислительных ресурсов. Мюллер может вносить в перехваченную криптограмму вредоносные изменения. В результате принятое Алексом сообщение может не совпадать с исходным.

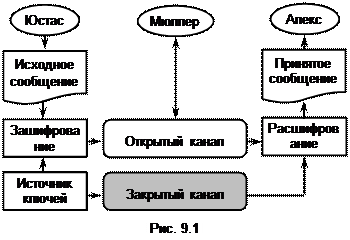
На рис. 9.1 показана классическая система коммуникации для передачи секретных сообщений.

Перед тем, как передать сообщение по открытому каналу связи, Юстас выполняет его зашифрование с помощью ключа. В результате в открытый канал поступает зашифрованное сообщение – криптограмма. Алекс, приняв эту криптограмму, расшифровывает ее с помощью того же ключа и в результате имеет принятое сообщение. Если Мюллеру не удалось внести в криптограмму изменений, то принятое сообщение совпадает с исходным.

Таблица 9.1
m	Am	An	n
	А	Г
	Б	Д
	В	Е
	Г	Ж
	Д	З
	Е	И
	Ж	Й
	З	К
	И	Л
	Й	М
	К	Н
	Л	О
	М	П
	Н	Р
	О	С
	П	Т
	Р	У
	С	Ф
	Т	Х
	У	Ц
	Ф	Ч
	Х	Ш
	Ц	Щ
	Ч	Ъ
	Ш	Ы
	Щ	Ь
	Ъ	Э
	Ы	Ю
	Ь	Я
	Э	А
	Ю	Б
	Я	В

Важно, что ключ передается от Юстаса к Алексу по специальному закрытому каналу связи, недоступному для Мюллера.

Следует отметить, что объем самих сообщений существенно превышает объем сведений о ключе, и передача их по закрытому каналу обошлась бы много дороже, чем по открытому каналу.

Рассмотрим пример конкретного шифра, в качестве которого выберем шифр Цезаря. Этот шифр римский император применял для засекречивания своих сообщений на латинском языке. Мы же адаптируем его к русскому языку, в алфавите которого 32 буквы (Е и Ё неразличимы и нет символа пробела).

Сам шифр приведен в табл. 9.1. В левом затемненном столбце табл. 9.1 находятся символы A_m алфавита исходного сообщения, в правом затемненном столбце – соответствующие им символы A_n зашифрованного текста (криптограммы). Нетрудно заметить, что правый столбец получен из левого путем циклического сдвига его символов вверх на три позиции. С каждым сдвигом на одну позицию символ из первой строки столбца перемещается в самую последнюю строку этого столбца, а все остальные символы сдвигаются на одну позицию вверх. Так за три сдвига в первой строке столбца A_n оказывается буква Г, а в последней – буква В.

Зашифрование исходного сообщения с помощью табл. 9.1 происходит так: каждая его буква A_m из правого затемненного столбца табл. 9.1 заменяется буквой A_n в соответствующей строке табл. 9.1. Расшифрование состоит в том, что каждая буква A_n криптограммы из левого затемненного столбца табл. 9.1 заменяется буквой A_m в соответствующей строке табл. 9.1.

Пример. Пусть исходным сообщением будет слово ДАННЫЕ. Юстас после применения к нему шифра Цезаря получает криптограмму ЗГРРЮИ. Алекс, имея табл. 9.1, по полученной криптограмме без труда восстановит исходное сообщение.

Формализованное описание шифра Цезаря со сдвигом на произвольное число k позиций получим, действуя с номерами m символов исходного сообщения столбца A_m и с номерами n символов A_n зашифрованного сообщения.

Правило (алгоритм) зашифрования – вычисление номера n символа зашифрованного сообщения по номеру m символа исходного сообщения и величине сдвига k – описывается такой формулой:

n=(m+k)_{mod M}. (9.1)

Число k называют ключом шифра Цезаря (в табл. 9.1. k=3), а M – количество символов алфавита (у нас M=32).

Алгоритм расшифрования секретного сообщения – получение номера m символа восстанавливаемого текста по номеру n символа криптограммы и значению ключа k – задается так:

m=(n+(M-k))_{mod M}. (9.2)

Напомним, что (A)_{mod M} – остаток от деления A на M нацело.

Понятно, что пользоваться неизменным ключом опасно. Поэтому Юстас и Алекс договариваются менять ключ k, к примеру, после передачи каждого сообщения. В этом случае можно сказать, что ключ порождается некоторым источником ключа (рис. 9.1).

Дата добавления: 2014-11-18