А. Аппроксимация функций

Тест 4. ФУНКЦИИ

ИНФОРМАТИКА И МАТЕМАТИКА

По дисциплине

Выполнил студент группы 9

(подпись) В. Чапаев

«25» ноября 2013 г.

N=38. W=(ДР)_{mod 20}=18.

Задача

По заданному выражению f(x) построить на отрезке [a,b] таблицу объемом n.

Выполнить линейную аппроксимацию этой табличной функции, найти приближенные значения y по аппроксимирующим формулам и точные значения y_T для x={x1,x2}.

Оценить погрешность аппроксимации.

f(x)=x´2^-x+5,

a=0, b=8, x1=1, x2=10.

Решение

Строим таблицу объемом n на отрезке [a,b] c шагом h.

n=4, h= =2.

xt₀=a=0, xt_i+1=xt_i+h, i= , xt_n=b=8, yt_i=f(xt_i), i= .

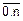Так получим табл.О1.

Таблица О1
i
xti
yti

Записываем формулы линейной аппроксимации табличной функции:

y=j_k(x)=yt_k+ ´(x-xt_k), (4.2)

k(x)= 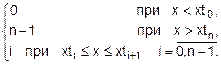(4.3)

Строим графики табличной функции {xt_i,yt_i} и заданной функции f(x). Для построения графика f(x) дополнительно вычислим ее значения для x={1, 3, 5, 7 9}: f(1)=16, f(3)=12, f(5)=5, f(7)=1.75, f(9)= @0.56.

Отмечаем эти значения на графике. Соединяем эти точки и точки, заданные табл. 1, плавной линией. Точки табличной функции {xt_i,yt_i} соединяем отрезками прямых (4.2). Отмечаем кривую надписью f(x), а отрезки прямых – надписями j_k(x), k= . Результат – на рис. 1.

Полагаем x=x1=1. Как видим (см. рис.1 или табл. О1), xt₀<x1<xt₁. Значит, по формуле (4.3) k1=0, и путем интерполяции находим приближенное значение y1 для x1:

y1=j₀(x1)=yt₀+ ´(x1-xt₀)=

=0+ 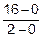´(1-0)=8.

Точное значение y1_T для x1 равно

y1_T=f(x1)=x´2^-x1+5=1´2^-1+5=16.

Наносим точку y1 на прямую j₀(x), а точку y1_T на кривую f(x) (рис. 1).

Погрешность аппроксимации составит

D1= 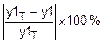= =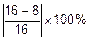50%.

Большая погрешность аппроксимации при x=x1=1 обусловлена тем, что на отрезке [0,2] прямая j₀(x) при n=4 сильно отличается от кривой f(x), и при x=x1=1 разность оказывается f(x1)-j₀(x1)=y1_T-y1 максимальной.

Для x=x2=10 имеет место x2>xt₃, и k2=3. Экстраполяция вперед:

y2=j₃(x2)=yt₃+ 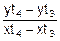´(x2-xt₃)=

=3+ ´(10-6)=-1.

Точное значение y2_T для x2 равно

y2_T=f(x2)= x´2^-x2+5=10´2^-10+5= 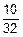=0.31.

Наносим точку y2 на прямую j₃(x), а точку y2_T на кривую f(x) (рис. 1).

Погрешность аппроксимации составит

D2= 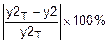= =420%.

Как видим, экстраполяция далеко за пределы таблицы нецелесообразна из-за огромных погрешностей.

Для уменьшения погрешностей аппроксимации нужно увеличивать объем таблицы n, то есть уменьшать ее шаг h.

Дата добавления: 2014-11-18