Элементы статистической обработки данных 14 страница

ПРИМЕЧАНИЕ. В криптографии (и не только там) убеждены, что логические операции сумма по модулю 2 (Å) и исключающее ИЛИ (XOR) – суть одно и то же. Дело в том, что для двух логических переменных таблицы истинности операций Å и XOR оказываются одинаковыми. Если же операндов больше двух, то таблицы истинности для операций Å и XOR будут существенно различными. И поэтому употребление названия XOR в качестве синонима Å некорректно.

Шифр гаммирования оказывается невскрываемым, если последовательность гамм представляет собою цепочку равновероятных случайных величин, а каждая гамма накладывается только один раз и только на один код (имеет место однократное гаммирование). В современных системах шифрования методом гаммирования последовательность гамм формируют программно. При этом получают цепочку псевдослучайных чисел. Дело в том, что элементы такой последовательности после некоторого их количества M повторяются, то есть эти элементы не являются строго случайными. Но в пределах одного периода их можно считать случайными. Для однократного гаммирования необходимо, чтобы число M было не меньше количества символов алфавита исходного текста. Каждую из программ для формирования гамм называют генератором псевдослучайных чисел.

Хорошими характеристиками в отношении периодичности и случайности получаемых гамм обладает генератор псевдослучайных чисел, который описывается таким соотношением:

G_i=(C1´G_i-1+C2)_{mod M}, i=1,2,…, M. (10.2)

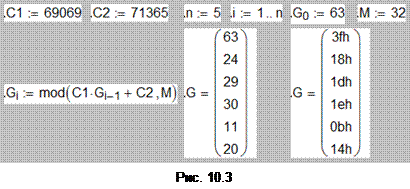
Как видим, каждая следующая гамма G_i получается из предыдущей G_i-1 путем умножения ее на константу C1, сложением полученного произведения с константой C2 и взятием этой суммы по модулю M. Для получения гаммы G₁ необходимо задать величину G₀ – порождающее число, которое не является гаммой, а представляет собою секретный ключ шифра гаммирования. Если C1 нечетно, а (C2)_{mod 4}=1, то период повторения гамм равен M. Десятилетия были потрачены математиками на поиск удовлетворительных значений для C1, C2 и M. В конце концов, остановились на значениях C1=69069, C2=71365, а M должно быть степенью 2.

Рассмотрим конкретный вариант построения криптосистемы с использованием метода гаммирования.

Для кодирования символов русского алфавита используем восьмиразрядные двоичные изображения их естественных номеров из табл. 9.1. В табл. 10.13 приведены шестнадцатеричные эквиваленты этих кодов.

В алфавите 32 символа. Поэтому полагаем M=32=2⁵.

Таблица 10.13

Am

А

Б

В

Г

Д

Е

Ж

З

И

Й

К

Л

М

Н

О

П

m

0A

0B

0C

0D

0E

0F

Am

Р

С

Т

У

Ф

Х

Ц

Ч

Ш

Щ

Ъ

Ы

Ь

Э

Ю

Я

m

1A

1B

1C

1D

1E

1F

Результат S_i наложения гаммы G_i на код Т_i символа исходного (зашифрованного) текста представим такой записью:

S_i=Т_iÅG_i. (10.3)

Пример. Методом гаммирования

а) зашифровать слово ГАММА,

б) расшифровать полученную криптограмму.

а) Результаты работы по зашифрованию исходного текста сведем в табл. 10.14.

Таблица 10.14
i
ТИi	Г	А	М	М	А
ТИmi			0C	0C
Gi		1D	1E	0B
ТЗmi	1C	1D
ТЗi	Ь	Э	Т	Е	Ф

В первой строке таблицы – номера i ее столбцов. Во вторую строку записываем символы ТИ_i исходного текста, а в третью – их шестнадцатеричные номера ТИm_i из табл. 10.13

Далее по формуле (10.2), в которой i= 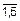, G₀=63, генерируем последовательность гамм G_i для каждого кода ТИm_i. Ниже на рис. 10.3 показан листинг вычислений по формуле (10.2) в системе компьютерной симуляции Mathcad. В первой строке заданы исходные данные, во второй записана формула (10.2) средствами Mathcad и выведены результаты вычислений. Вычисления ведутся в десятичной системе счисления. В последнем столбце второй строки листинга результаты переведены в шестнадцатеричную систему. Эти результаты и записываем в четвертую строку табл. 10.14. Напомним, что G₀=63=3F не является гаммой.

Для каждой пары кодов ТИm_i и G_i выполняем операцию наложения гаммы (10.3) (напомним (см. гл. 2, табл. 2.1), что одна шестнадцатеричная цифра – это четверка двоичных цифр и наоборот):

i=1.	ТИm1=03=
		Å	Å	Å	Å	Å	Å	Å	Å
	G1=18=
	S1=									=1C

ТЗm₁=1C. ТЗ₁=Ь.

i=2.	ТИm2=00=
		Å	Å	Å	Å	Å	Å	Å	Å
	G2=1D=
	S2=									=1D

ТЗm₂=1D. ТЗ₂=Э.

i=3.	ТИm3=0C=
		Å	Å	Å	Å	Å	Å	Å	Å
	G3=1E=
	S3=									=12

ТЗm₃=12. ТЗ₃=Т.

i=4.	ТИm4=0C=
		Å	Å	Å	Å	Å	Å	Å	Å
	G4=0B=
	S4=									=05

ТЗm₄=05. ТЗ₄=Е.

i=5.	ТИm5=00=
		Å	Å	Å	Å	Å	Å	Å	Å
	G5=14=
	S5=									=14

ТЗm₅=14. ТЗ₅=Ф.

Полученные коды ТЗm_i записываем в пятую строку табл. 10.17.

Пользуясь табл. 10.16, для каждого кода ТЗ8_i находим соответствующий ему символ ТЗ_i зашифрованного текста и записываем его в шестую строку табл. 10.17.

В результате получим криптограммуЬЭТЕФ.

б) Результаты действий по расшифрованию криптограммы ЬЭТЕФ сведем в табл. 10.15, которая подобна табл. 10.14. Но во второй строке табл. 10.15 записаны символы ТЗ_i зашифрованного текста, а в третьей – их шестнадцатеричные эквиваленты ТЗm_i.

Таблица 10.15
i
ТЗi	Ь	Э	Т	Е	Ф
ТЗmi	1C	1D
Gi		1D	1E	0B
ТИmi			0C	0C
ТИi	Г	А	М	М	А

Для каждой пары кодов ТЗm_i и G_i выполняем операцию наложения гаммы (10.3):

i=1.	ТЗm1=1C=
		Å	Å	Å	Å	Å	Å	Å	Å
	G1=18=
	S1=									=03

ТИm₁=03. ТИ₁=Г.

i=2.	ТЗm2=1D=
		Å	Å	Å	Å	Å	Å	Å	Å
	G2=1D=
	S2=									=00

ТИm₂=00. ТИ₂=А.

i=3.	ТЗm3=05=
		Å	Å	Å	Å	Å	Å	Å	Å
	G3=0B=
	S3=									=0C

ТИm₃=0C. ТИ₃=М.

i=4.	ТЗm4=05=
		Å	Å	Å	Å	Å	Å	Å	Å
	G4=0B=
	S4=									=0C

ТИm₄=0C. ТИ₄=М.

i=5.	ТЗm5=14=
		Å	Å	Å	Å	Å	Å	Å	Å
	G5=14=
	S5=									=00

ТИm₅=00. ТИ₅=А.

Полученные коды ТИm_i записываем в пятую строку табл. 10.18.

Пользуясь табл. 10.13, для каждого кода ТИm_i находим соответствующий ему символ ТИ_i расшифрованного текста и записываем его в шестую строку табл. 10.15.

В результате получим исходный текстГАММА.

Этим примером мы проиллюстрировали тот факт, что гаммирование – унифицированная процедура зашифрования и расшифрования текстов.

Вопросы и задачи для самоконтроля

1. Изложить суть метода перестановки на примере шифра вертикальной перестановки.

2. С помощью шифра вертикальной перестановки с ключами K1=4, 1, 6, 2, 5, 3 и K2=4,2,3,5,7,1,6 зашифровать исходный текст

КЛЮЧИ ДОЛЖНЫ ВЫБИРАТЬСЯ СЛУЧАЙНО.

3. Изложить суть метода гаммирования.

Пояснить смысл операции сложения по модулю 2 и причины выбора этой операции для реализации метода гаммирования.

Описать назначение генератора псевдослучайных чисел и выбор его параметров.

4. Методом гаммирования

а) зашифровать слово АСУ,

б) расшифровать полученную криптограмму.

В качестве гамм использовать первые три гаммы из табл. 10.17.

5. Выполнить ДКЗ: Тест 10. МЕТОДЫ КРИПТОГРАФИЧЕСКОЙ ЗАЩИТЫ ИНФОРМАЦИИ.

ОТВЕТЫ К ЗАДАЧАМ

Каждая глава завершается параграфом «Вопросы и задачи для самоконтроля». Читателю предлагается самостоятельно ответить на вопросы и решить задачи. Далее приведены ответы и решения к наиболее сложным задачам.

РАЗДЕЛ I.

ОСНОВАНИЯ МАТЕМАТИКИ

Глава 1. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ

6. а) AÈ(ùAÇB)=<3>=(AÈùA)Ç(AÈB)=

=<5>=WÇ(AÈB)=<4’>=AÈB.

б) (AÇB)È(AÇùB)=<3’>=AÇ(BÈùB)=

=<5>=AÇW=<4’>=A.

в) ù(AÈB)=(ùAÇùB). Решаем задачу графически (рис. в). Сформируем отдельно левую ù(AÈB) и правую (ùAÇùB) части утверждения. Как видим, они одинаковы. Значит, утверждение ù(AÈB)=(ùAÇùB) верно.

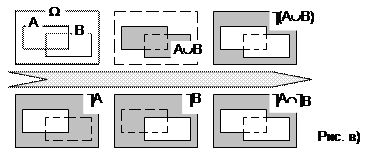
г) Утверждение ù(AÇB)=(ùAÈùB) верно, потому что оно дуально только что доказанному утверждению в).

7. 2=A\(BÈC); 6=(AÇB)\C; 8=AÇBÇC.

9. а) ИБÈЗИ; б) ИБÇЗИ;

в) ИБ\ЗИ; г) ЗИ\ИБ.

Глава 2. ЧИСЛА

4. (1000)_mod19=12, (1000)_mod10=0, (1000)_mod6=4.

(73)_mod19=16, (73)_mod10=1, (73)_mod6=1.

(7)_mod19=7, (7)_mod6=7, (7)_mod10=3.

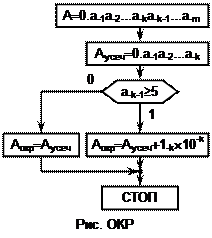
6. См. рис. ОКР.

8. Некомплект судей:

а) в Гончарове: 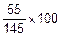=38%;

б) в Тургеневе: 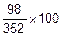=28%.

Значит, в Гончарове дела хуже.

Глава 3. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ

5. д) Обозначим высказывание «если a>b, а b>c, то v=w» как A, a>b – как x₀, b>c – как x₁, v=w – как x₂. Тогда

A=(x₀Ùx₁)®x₂ (табл. 5).

8. R=(ùx₂Ùùx₁Ùùx₀)Ú(ùx₂Ùùx₁Ùx₀)Ú(ùx₂Ùx₁Ùùx₀)Ú(ùx₂Ùx₁Ùx₀)Ú

Ú(x₂Ùùx₁Ùùx₀)Ú(x₂Ùùx₁Ùx₀)Ú(x₂Ùx₁Ùùx₀)Ú(x₂Ùx₁Ùx₀)=á9ñ=

=(ùx₂Ùùx₁)Ú(ùx₂Ùx₁)Ú(x₂Ùùx₁)Ú(x₂Ùx₁)=á9ñ=ùx₂Úx₂=á5ñ=1.

9. б) ((A®ùA)®ùA)=((ùAÚùA)®ùA)=<7>=

=(ùA®ùA)=ùùAÚùA=<12>=AÚùA=<5>=1.

Таблица 5,г
x2	x1	x0	x0Ùx1	Y

Остальные утверждения доказываются аналогично.

РАЗДЕЛ II.
ОСНОВЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА

Глава 4. ФУНКЦИИ

	Таблица ПОФ
y=2^-^x	x	-1		+1	+2	+3	y	y=-log2(x)
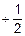
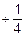
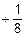
y	+2	+1				x

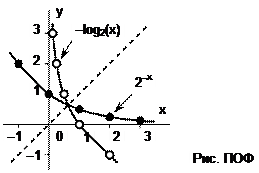
4. Делаем замену: x=2^-y. Отсюда y=-log₂(x) – функция, обратная исходной. Строим таблицу прямой функции. Таблицу обратной функции получим, поменяв местами строки таблицы прямой функции (табл. ПОФ).

По данным этой таблицы строим графики прямой и обратной функций (рис. ПОФ).

15. а)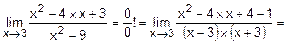

.

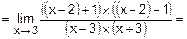
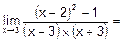
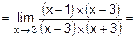
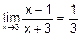в) = =-¥.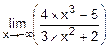

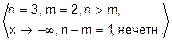г) 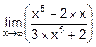=án=5, m=5, n=m, a_n=1, b_m=3ñ= .

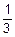д) = =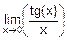

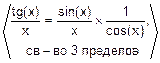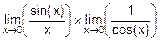= =1´ =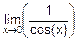

=áпрямая подстановкаñ=1.

е) = =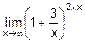

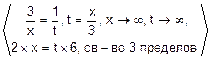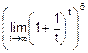= =e⁶=403.43.

Глава 5. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ

2. в) y’= ,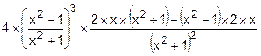

д) y’=(arccos(x))’= =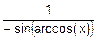

= = .

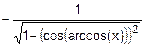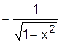9. б) e^1.05=e^1+0.05=e^x+Dx=

= á e^x+Dx=e^x+(e^x)’´Dx=e^x+e^x´Dx=e^x´(1+Dx) ñ =

=e´1.05=2.854.

Глава 6. ОСНОВЫ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ

8. б) F= .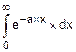

Этап 1.

F(x)= =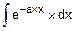

= =

= .

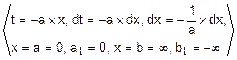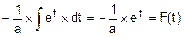Этап 2.

F=F_NL= = = .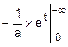

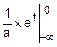10. а) По формуле Ньютона-Лейбница.

F= .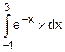

Этап 1.

F(x)= 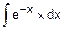=á-x=t, dt=-dx, dx=-dtñ=

= = .

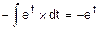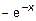Этап 2.

F=F_NL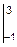=-e^-x =e^-x 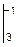=e¹-e^-3=2.72-0.05=2.67.

б) Методом Рунге-Ромберга по формуле трапеций.

0. Cтроим таблицу {xt_i, yt_i} функции f(x) на отрезке [a, b] объемом n=4:

h= 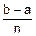=1, xt₀=a=-1, xt_i+1=xt_i+h, i= 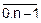, yt_i=f(xt_i), i= .

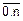i
xti	-1.0	0.0	1.0	2.0	3.0
yti	2.72	1.00	0.37	0.14	0.05
j

1. По таблице {xt_i, yt_i} вычисляем значение F_h:

F_h= =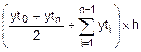

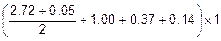= =2.89.

2. Формируем таблицу {xt2_j, yt2_j}. Выделяем в таблице {xt_i, yt_i} столбцы с четными номерами, заново их нумеруем подряд j= 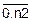, находим n2= 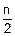=2, h2=2´h=2.

По таблице {xt2_j, yt2_j} вычисляем значение F_2h:

F_2h= =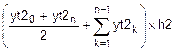

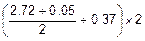= =3.51.

3. Вычисляем поправку Рунге:

PR= 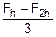=-0.20.

4. Вычисляем значение интеграла по формуле Рунге-Ромберга:

F=F_RR=F_h+PR=2.69.

5. Проверяем контрольное условие:

ïF_NL-F_RRï=0.02<ïPRï=0.20.

РАЗДЕЛ III.
ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ

Глава 7. ПОНЯТИЕ ВЕРОЯТНОСТИ

6. Дополним картину еще одним из возможных результатов – ничьей Н. Тогда W={A,B,H}. По смыслу задачи события A, B и H – несовместные (результатом игры может быть только одно из этих событий): A´B=A´H=B´H=Æ. Поэтому

а) событие ùB (второй не выиграл) означает, что выиграл первый или партия закончилась вничью, то есть ùB=A+H. Точно так и событие ùA=B+H,

б) событие ùA´ùB (не выиграл первый и не выиграл второй) – однозначно ничья:

ùA´ùB=á10’ñ=ù(A+B)=áA+B=ùHñ=ùùH=á12ñ=Н.

в) событие ùA+ùB (не выиграл первый, или не выиграл второй, или не выиграл ни тот, ни другой) означает, что возможен любой исход игры. Действительно,

Дата добавления: 2014-11-18