Элементы статистической обработки данных 15 страница

ùA+ùB=ù(A´B)=áA´B=Æñ=ùÆ=W.

12. а) Сухов выберет все три вопроса, на которые знает ответы:

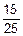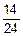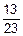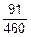´ ´ = @0.198.

13. Проверяется три дела. Событие «взято дело о краже» обозначим как К, событие «взято дело не о краже» – как Н.

а) Тогда событие А – «среди трех взятых на проверку дел два о краже» суть:

А=К´К´Н+К´Н´К+Н´К´К,

вероятность которого вычисляют так:

P(A)= + + =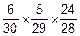

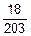= @0.089.

16. а) Событие второй билет выигрышный В2 наступает при выполнении двух гипотез: первым был тоже выигрышным В1, первым был невыигрышным Н1. По формуле полной вероятности вычисляем

P(В2)=P(В1)´P(В2ïВ1)+P(В2)´P(В2ïН1)=

= ´ + ´ = .

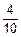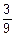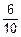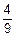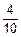б) По формуле Байеса апостериорная вероятность гипотезы В1 суть

P(В1ïВ2)= = : = .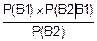

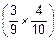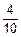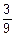18. Вероятность того, что клиент берет вклад p= 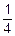, вероятность того, что вклад он брать не будет q= .

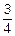а) это событие укладывается в схему Бернулли при n=6, m=2:

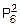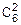= ´p²´q⁴= ´ ´ =

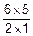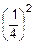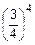=5´3⁵´ 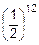= 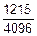@0.3.

19. Данный случайный эксперимент укладывается в схему Бернулли с параметрами p=0.2 (20% попаданий) и q=0.8. Событие «хотя бы один раз»=ХО противоположно событию «ни одного раза»=НО. По условию задачи P(ХО)=0.9, а P(НО)=1-P(ХО)=0.1. Но с другой стороны, по формуле Бернулли P(НО)= 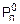= 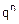. Значит,

0.1= 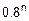, ln(0.1)=n´ln(0.8), n= 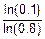=10.32.

Для того чтобы с вероятностью 0.9 поразить мишень потребуется 11 выстрелов.

Глава 8. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

8. Испытание укладывается в схему Бернулли с параметрами: n=3, m= , p=0.2, q=0.8. Пользуясь формулой Бернулли

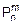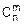= ´pⁿ´q^n-m,

построим ряд распределения для возможного количества m фальшивых купюр (табл. 8), а потом найдем и числовые характеристики этой СВ.

Таблица 8
m
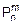
	0.512	0.384	0.096

M[m]= 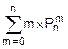=0.6;

D[m]= 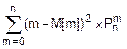=0.48; s= 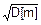=0.69.

9. M[X]=m_x= 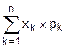=2´0.2+5´0.3+8´0.4+19´0.1=7.0.

D[X]=D_x=M[(X-m_x)²=

=(2-7)²´0.2+(5-7)²´0.3+(8-7)²´0.4+(19-7)²´0.1=21.

s_x= 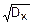= =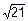4.6.

10. Имеем

f(x)=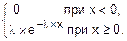

Проверим условие нормировки для f(x): площадь под кривой f(x) на всей числовой оси равна единице:

FN= 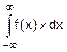= =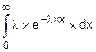1.

Этап 1.

FN(x)= = =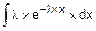

= = = .

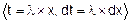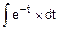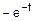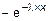Этап 2.

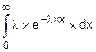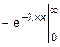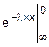= = =1.

а) По определению (8.6) F(x)= .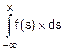

В нашем случае

F(x)=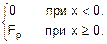

Здесь

F_p(x)= .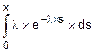

Этап 1.

F_p(s)= = =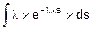

= =

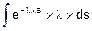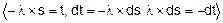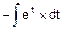= =-e^-l´s.

Этап 2.

F_p(x)= 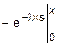= =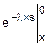1-e^-l´x.

Таким образом,

F(x)=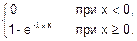

б) По определению (8.13) m_x= .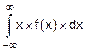

В нашем случае

m_x= .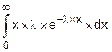

Этап 1.

Fm(x)= =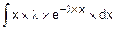

= =

= =

= =

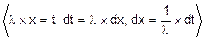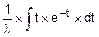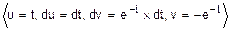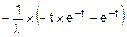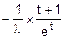= = =Fm(t).

x=0, t=0, x®¥, t®¥.

m_x= = =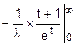

= =

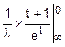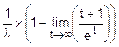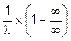= !=áправило Лопиталяñ=

= = = .

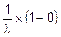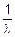По определению (8.14) D_x= .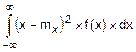

В нашем случае

D_x= =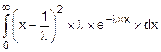

= =

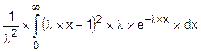=ál´x=t, dt=l´dxñ= .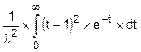

Этап 1.

FD(x)= =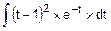

= =

= =

= =

= =

= =

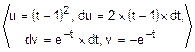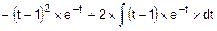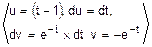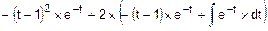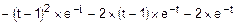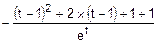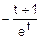= = =FD(t).

x=0, t=0, x®¥, t®¥.

Этап 2.

D_x= = = .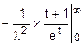

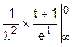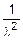По определению (8.10) s_x= = .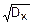

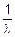Таблица Ф
x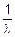
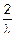
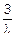
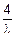
l´e^-^l^´^x	l	0.37´l	0.14´l	0.05´l	0.02´l
1-e^-^l^´^x		0.63	0.86	0.95	0.98

в) Составим таблицу значений для f(x) и F(x) для 0<x< 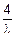(табл. Ф).

По данным этой таблицы построим графики этих функций (рис. Ф) и отмечаем на них значения m_x и s_x.

г) По определению (8.6)

P(a<X<b)=F(b)-F(a).

В нашем случае

a=m_x-s_x=0, m_x+s_x= .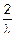

Значит,

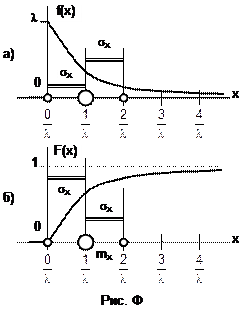
P(0<X< 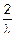)=F(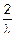)-F(0)=0.86.

18. Очевидно, что и в опыте с первой урной, и в опыте со второй H_{после опыта}=0 (сообщение о цвете вынутого шара получено). Значит, количество информации о цвете шара равно энтропии каждого опыта I=H_{до опыта}.

В опыте с первой урной имеем: p₁=0.1, p₂=0.2, p₃=0.3, p₄=0.4, и энтропия вычисляется по формуле Шеннона (8.20):

H_{до опыта}=-(0.1´log₂(0.1)+ 0.2´log₂(0.2)+

+0.3´log₂(0.3)+ 0.4´log₂(0.4))=1.85.

В опыте со второй урной исходы равновероятны p₁=p₂=p₃= p₄=0.25, и энтропия вычисляется по формуле (8.21) для N=4:

H_{до опыта}=log₂(4)=2.00.

Глава 9. ОСНОВЫ КРИПТОГРАФИЧЕСКОЙ
ЗАЩИТЫ ИНФОРМАЦИИ

3. а) криптограмма: ЕФЦПЯЛ.

Глава 10. МЕТОДЫ КРИПТОГРАФИЧЕСКОЙ
ЗАЩИТЫ ИНФОРМАЦИИ

2. Имеем R=32, M=5, N=7. Действуем по алгоритму зашифрования методом вертикальной перестановки.

Разбиваем блок исходного текста на M=5 групп (табл. Зад 2).

Таблица Зад 2

К

Л

Ю

Ч

И

Э

Д

О

Л

Ж

Н

Ы

Э

В

Ы

Б

И

Р

А

Т

Ь

С

Я

Э

С

Л

У

Ч

А

Й

Н

О

Создаем и заполняем таблицу перестановок (табл. П).

Таблица П
	С	Я	Э	С	Л	У	Ч
	К	Л	Ю	Ч	И	Э	Д
	О	Л	Ж	Н	Ы	Э	В
	А	Й	Н	О
	Ы	Б	И	Р	А	Т	Ь

Считываем содержимое таблицы перестановок по столбцам и получаем криптограмму:

4.	а)	i
ТИi	А	С	У
ТИmi
Gi		1D	1E
ТЗi	Ш	М	Н

УЭЭТЯЛЛЙБЮЖНИСКОАЫСЧНОРЧДВЬЛИЫА.

Получили криптограмму:

ШМН.

В случае злостного уклонения осужденного от отбывания исправительных работ суд может заменить неотбытое наказание лишением свободы из расчета один день лишения свободы за три дня исправительных работ.

(УК РФ, Ст. 50, п. 4)

ПРИЛОЖЕНИЕ
ТЕСТЫ

Тест [англ. test –контрольная работа, проверка, экзамен] – задача, которую предлагается решить обучаемому для оценки его знаний и умений путем сравнения полученных им результатов с известным решением (с эталоном).

Каждый тест по данной дисциплине представляет собою домашнее контрольное задание ДКЗ, которое студент выполняет в часы самостоятельной работы после изучения очередной темы учебной программы по дисциплине.

Студент выполняет только один вариант номер W каждого теста:

W=(N)_{mod 20},

где N – номер студенческого билета: ¼¼/N.

Напомним, что (A)_{mod M} – остаток от деления числа А на модуль M нацело.

Отчет по ДКЗ оформляется по образцу, который приведен ниже. Отчет должен содержать:

вычисление номера варианта W,

условие задачи,

решение.

Решение задачи следует сопровождать необходимыми пояснениями, иллюстрациями, ссылками на формулы, аксиомы, теоремы и т.п. из учебника, конспекта лекций.

Аккуратно оформленный (пусть и от руки, но по образцу(!)) отчет по ДКЗ предоставляется преподавателю для оценки.

Кафедра информационного права,

информатики и математики

ДОМАШНЕЕ КОНТРОЛЬНОЕ ЗАДАНИЕ

Дата добавления: 2014-11-18