Элементы статистической обработки данных 13 страница

В криптографии считается, что алгоритмы зашифрования и расшифрования не являются секретными, секретным является значение k ключа.

Пример. Рассмотрим действия Мюллера, в руках которого криптограмма ЗГРРЮИ, и ему известно, что она получена по алгоритму (9.1), а расшифровывается по алгоритму (9.2). Мюллер пытается по содержанию криптограммы определить ключ.

Всякую попытку определить ключ по криптограмме называют атакой на шифр, а удачную атаку называют взломом шифра.

Самая очевидная стратегия действий Мюллера – последовательный перебор всех возможных значений ключа k= 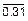и анализ результатов подстановки их в формулу (9.2).

В табл. 9.2 сведены некоторые из полученных им результатов. Как видим, довольно быстро Мюллер установил, что k=3.

Таблица 9.2
k	результат
	ЗГРРЮИ
	ЖВП…
	ЕБОО…
	ДАННЫЕ
	ГВМ…
	Ъ…
	Ы…
	Ь…
	КЖ…
	ЙЕУ…
	ИДТТ…

Его задача существенно облегчается тем обстоятельством, что очередное значение k отбрасывается после применения его к трем-четырем первым буквам криптограммы, поскольку полученные сочетания букв результата не имеют смысла в русском языке.

А значения k=13, 14, 15 отбрасываются вместе с первой полученной буквой результата, так как в русском языке нет слов, начинающихся с Ъ, Ы, Ь.

Шифр Цезаря обладает низкой стойкостью к взлому. Причина нестойкости шифров, подобных шифру Цезаря, обусловлена тем, что алфавит русского языка (да и любого другого естественного языка) имеет такое свойство: его буквы появляются в осмысленных текстах с разной вероятностью. В русских текстах чаще всего (с вероятностью 0.094) встречается буква О, а реже всего (с вероятностью 0.002) – буква Э. Имеют различные вероятности появления в осмысленных текстах и сочетания из двух букв (биграмм), из трех и более букв. В нашем примере Мюллер использовал тот факт, что большинство из полученных сочетаний букв имеют равную нулю вероятность появления в словах.

Взломать шифр Цезаря можно еще быстрее, если знать, что биграмма НН встречается чаще всех других пар одинаковых букв. В криптограмме имеем пару РР. Предположим, что в исходном сообщении ей отвечает пара НН. Проверка этого предположения сразу раскрывает значение ключа k. Для буквы Р значение n=16 получено по формуле (9.1) из номера m=13 для буквы Н:

16=(13+k)_{mod M}. (9.3)

Функция (A)_{mod M} принимает значения 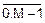с периодом M=32. Поэтому уравнение (9.3) имеет бесконечное число решений. Первым из них будет то, которое получается при 13+k<M=32:

16=13+k, k=3..

Следующее решение уравнения (9.3) отстоит от k=3 на величину M=32 и равно 35. Оно и все последующие решения лежат за пределами возможных значений k= 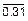и их отбрасывают. Применив значение k=3 к символам криптограммы, получаем осмысленный результат, то есть взламываем шифр.

Рассмотрим еще один пример. Юстас должен передать Алексу пятизначный номер ячейки камеры хранения, где для него вложена посылка. Положим, что в номерах ячеек одинаковые цифры не допускаются. Юстас зашифровывает номер с помощью шрифта Цезаря, приспособленного к алфавиту из десяти арабских цифр, а именно, теперь в формулах (9.1) и (9.2) используется модуль M=10. И пусть у Юстаса получилась такая криптограмма: 52481.

Таблица 9.3
k	результат	k	результат

Мюллер пытается узнать исходный номер ячейки перебором всех возможных значений ключа k= . Результаты его работы представлены в табл. 9.3. Как видим, ни одному из полученных результатов нельзя отдать предпочтения, то есть шифр взломать невозможно.

Объясним этот феномен. В данный разряд номера можно записать:

§ или любую из десяти цифр, если все пять разрядов его еще пусты,

§ или любую из девяти цифр, если занят один из пяти разрядов,

§ или любую из восьми цифр, если заняты два из пяти разрядов,

§ или любую из семи цифр, если заняты три из пяти разрядов,

§ или любую из шести цифр, если свободен один из пяти разрядов.

Значит, вероятность появления любой из десяти цифр в любом из пяти разрядов номера равна 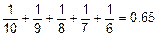. Сообщения из равновероятных символов обладают максимальной энтропией. А шифры, построенные на алфавите из таких символов, нельзя взломать.

9.2. Основные понятия и определения

Итак, мы ознакомились с принципами, основными понятиями и определениями криптографии. Систематизируем полученные сведения.

В качестве информации, подлежащей зашифрованию и расшифрованию, выступают данные различной природы.

Алфавит – конечное множество символов, используемых для представления данных.

Текст – упорядоченная последовательность символов алфавита.

Кодирование – представление информации символами того или иного алфавита. Шифр Цезаря применялся нами к информации, записанной средствами русского алфавита. Для того, чтобы формализовать описание алгоритмов шифра Цезаря, пришлось сопоставить каждому символу его номер – код и оперировать с этими номерами, то есть с числами. Любая обработка данных посредством компьютеров предполагает представление этих данных в двоичном алфавите {0,1}. Двоичное кодирование данных любой природы позволяет оперировать с такими кодами как с двоичными числами.

Зашифрование – преобразование открытых данных (исходного текста) в закрытые (в криптограмму) при помощи ключа шифра.

Расшифрование – обратное преобразование зашифрованных данных в открытые при помощи ключа шифра.

Зашифрование и расшифрование объединяют термином криптографические преобразования или шифрование.

Шифр или криптографическая система – совокупность (семейство) преобразований открытого текста в зашифрованный и обратного преобразования криптограммы в исходное сообщение. И прямое, и обратное криптографическое преобразование задается своим алгоритмом.

Ключ – конкретное секретное значение непременного параметра криптографической системы. Это значение обеспечивает выбор одного преобразования из совокупности возможных для данной системы преобразований. Обычно ключ представляет собою последовательность символов алфавита. Следует различать термины ключ и пароль. Пароль, также как и ключ, является секретной последовательностью символов алфавита, но используется не для криптографических преобразований, а дли идентификации субъектов.

Стойкость криптосистемы – свойство шифра, которое характеризует его защищенности от вскрытия. В качестве показателя стойкости криптосистемы могут выступать:

§ тот минимальный объем зашифрованного текста, статистический анализ которого позволяет взломать шифр. Таким образом, стойкость шифра определяет допустимый объем открытых данных, который зашифровывается при помощи одного ключа,

§ вероятность взлома шифра путем перебора всех возможных значений ключа за заданное время с заданными ресурсами,

§ объем вычислительной работы или время (при заданных ресурсах), необходимые для взлома шифра с заданной вероятностью.

Для современных криптографических систем защиты информации сформулированы следующие общепринятые требования.

1. В секрете держится только ключ криптографической системы, открытость алгоритмов шифрования не должно снижать стойкости шифра. Это фундаментальное требование называют принципом Керкхоффса по имени голландского криптографа, который сформулировал его в XIX веке. К. Шеннон (независимо от А. Керкхоффса) изложил этот принцип более компактно: «Враг знает систему».

2. Зашифрованное сообщение поддается расшифрованию только при помощи ключа.

3. Шифр должен оставаться стойким и в том случае, если противнику известно достаточно большое количество исходных текстов и соответствующих им криптограмм.

4. Объем вычислительной работы, необходимый для взлома шифра путем перебора всех возможных ключей, должен иметь строгую нижнюю границу, которая лежит выше вычислительных возможностей современных компьютеров и компьютерных сетей.

5. Незначительное изменение ключа или исходного текста должно приводить к существенному изменению вида зашифрованного текста. Это позволяет обнаруживать случайные искажения ключа или исходного текста.

Незначительные изменения в тексте криптограммы должны вызывать значительные изменения в расшифрованном тексте по сравнению с исходным. Это позволяет обнаруживать как случайные (из-за помех в открытом канале), так и преднамеренные изменения в криптограмме.

6. Структурные элементы алгоритмов криптографических преобразований должны быть неизменными.

7. Длина криптограммы должна быть равна длине исходного сообщения

8. Дополнительные символы, вводимые в исходное сообщение до начала его зашифрования, должны быть полностью и надежно скрыты в криптограмме. Дополнительные символы могут понадобиться для выравнивания длины исходного текста и длины криптограммы.

9. Не должно быть простых, легко устанавливаемых зависимостей между ключами, последовательно используемыми в процессе криптографических преобразований.

10. Любой ключ из множества возможных должен обеспечивать надежную защиту данных. Другими словами, среди возможных ключей не должно быть слабых значений.

В отношении противника в криптографии принимаются следующие допущения.

Ø Противник знает алгоритмы криптографических преобразований, но не знает ключа шифра.

Ø Противнику доступны все зашифрованные тексты. Он имеет доступ к некоторым исходным текстам, и у него есть соответствующие этим текстам криптограммы.

Ø Противник имеет в своем распоряжении вычислительные, временные и иные ресурсы, объем которых эквивалентен потенциальной ценности информации, которая может быть добыта в результате взлома шифра.

По степени сложности различают три уровня криптоатак.

ü Атака на криптограмму. Для взлома шифра используют перебор всех возможных значений ключа или статистические характеристики алфавита сообщений.

ü Атака на пару криптограмма – исходный текст.

ü Атака на пару исходный текст- криптограмма.

В двух последних случаях противник пытается взломать шифр путем анализа взаимосвязей между исходным текстом и соответствующей ему криптограммой.

Вопросы и задачи для самоконтроля

1. Раскрыть понятие криптография, описать работу в классической системе коммутации для передачи секретных сообщений.

2. Пояснить алгоритмы зашифрования и расшифрования шифром Цезаря с ключом k. Пояснить, в чем причина низкой стойкости шифра Цезаря.

3. Шифром Цезаря с ключом k=15

а) зашифровать сообщение

ЦЕЗАРЬ,

б) расшифровать полученную криптограмму.

4. Дать определения основным понятиям криптографии: алфавит, текст, кодирование, шифр, ключ, зашифрование, расшифрование.

5. Дать определение стойкости криптосистемы, перечислить основные показатели стойкости криптосистемы.

6. Перечислить основные требования к криптосистемам.

Глава 10. МЕТОДЫ КРИПТОГРАФИЧЕСКОЙ
ЗАЩИТЫ ИНФОРМАЦИИ

За всю историю криптографии разработано много методов защиты информации. Каждый из этих методов состоит в том, что при зашифровании одному символу исходного текста ставится в соответстве по определенному правилу другой символ. При расшифровании полученной криптограммы выполняется обратная замена ее символов символами исходного текста тоже по некоторму правилу.

Рассмотренный нами шифр Цезаря с ключом k – пример моноалфавитной подстановки. Как мы уже знаем, симвлы исходного текста заменяются взятыми из одного и того же алфавита, которые сдвинуты на k позиций. Расшифровка криптограммы производится сдвигом на k позиций в обратном направлении. Этот метод отличается низкой стойкостью. Зашифрованный текст имеет те же статистические характеристики, что и исходный. Если в руках противника оказывается криптограмма достаточной длины, то он имеет возможность получить достоверные оценки вероятностей появления символов и взломать шифр. Количественно стойкость моноалфавитной подстановки оценивается в 20-30 символов. Поэтому она применяется лишь для шифрования коротких сообщений.

Изучим некоторые из методов криптографической защиты информации с высокой стойкостью.

10.1. Методы перестановки

При шифровании перестановкой меняется порядок следования символов исходного текста. Перестановка получается за счет того, что запись исходного (зашифрованного) текста в специальную таблицу производится по одному пути, а чтение зашифрованного (расшифрованного) текста – по другому пути.

Рассмотрим метод так называемой вертикальной перестановки. В этой системе шифрования используется прямоугольная таблица перестановок размером в M строк и N столбцов. Значения M и N секретны. Поэтому еще задают два секретных ключа. Ключ K1 длиною в M позиций, который представляет собою случайную последовательность натуральных чисел из ряда 1, 2,…, M. Числа ключа K1 нумеруют строки таблицы перестановок. Ключ K2 длиною в N позиций тоже представляет собою случайную последовательность натуральных чисел из ряда 1, 2,…, N. Числа ключа K2 нумеруют столбцы таблицы перестановок.

Стойкость шифра вертикальной перестановки определяется размером его таблицы перестановок. Количество ключей K1 равно числу перестановок из M элементов: P_M=M! Количество ключей K2 равно числу перестановок из N элементов: P_N=N! А общее пространство ключей у шифра вертикальной перестановки составляет M!´N! С увеличением длины L ключа величина L! резко возрастает, и уже при L=M=N=16 она составляет

16!´16!»1.4´10²⁶»2⁹⁰.

Задача прямого перебора такого количества ключей практически не решается даже современными вычислительными средствами.

Для зашифрования по методу вертикальной перестановки исходный текст разделяют на блоки длиною в R=M´N символов. При этом длина последнего из блоков может оказаться такой, что R<M´N.

Таблица перестановок заполняется по строкам. Для этого блок исходного текста разбивается на группы символов длиною в n=N символов. Если R=M´N, то таких групп ровно M. Группы нумеруются в естественном порядке 1, 2, …, M.

Когда последний блок окажется таким, что R<M´N, то в последней группе этого блока окажется n<N символов. Значения M и N подбирают так, чтобы в последнем блоке первые M-1 групп имели бы длину точно в N символов и только одна последняя группа номер M – длину в n<N символов. Для этого значения R, M и N для последнего блока должны отвечать условиям

(M-1)´N<R≤M´N. (10.1)

Алгоритм зашифрования блока исходного текста длиною в R символов шифром вертикальной перестановки задается такой последовательностью шагов.

0. Создают заготовку таблицы перестановок размером в M строк и N столбцов. Слева от первого ее столбца записывают номера строк, заданные ключом K1, а над первой строкой – номера столбцов таблицы, заданные ключом K2.

1. Блок исходного текста разделяют на группы длиною в N символов каждая. Группы нумеруются в естественном порядке 1. 2….. M. Если R<M´N, то в последней группе с номером M окажется n<N символов.

2. Каждую группу символов записывают в свою строку таблицы перестановок, номер этой строки задан ключом K1.

3. Содержимое заполненной таблицы считывается по столбцам в том порядке, который задан ключом K2 в один блок зашифрованного текста.

При R<M´N в строке с номером M первые n ячеек будут заполнены символами последней группы блока исходного текста, а остальные N-n ячеек окажутся свободными. Их не следует заполнять даже произвольными символами алфавита. В противном случае длина блока зашифрованного текста будет больше длины блока исходного текста. А это в криптографии недопустимо.

После зашифрования всех блоков исходного текста полученные блоки зашифрованного текста объединяются в одну криптограмму, которая передается по назначению.

Пример. Шифр вертикальной перестановки задан таблицей перестановок размером в 5 строк и 7 столбцов с ключами K1=2, 5, 1, 3, 4 и K2=5, 1, 4, 7, 2, 6, 3.

Зашифровать фразу

ПРИМЕР ВЕРТИКАЛЬНОЙ ПЕРЕСТАНОВКИ,

в которой символ пробела заменить буквой Э.

В исходном тексте 32 символа, а в таблице перестановок будет M=5 строк, N=7 столбцов, то есть M´N=35 ячеек. Значит, исходный текст представляет собою один блок, длина которого R=32 отвечает условиям (10.1): (M-1)´N=28<32≤M´N=35.

Таблица 10.6
	В	Е	Р	Т	И	К	А
	О	В	К	И
	П	Р	И	М	Е	Р	Э
	Л	Ь	Н	О	Й	Э	П
	Е	Р	Е	С	Т	А	Н

0. Создаем заготовку таблицы перестановок для заданного шифра (это пока пустая табл. 10.6).

1. Блок исходного текста разделяем на группы длиною в N символов (табл. 10.7). Как видим, первые четыре группы имеют длину по 7 символов, а пятая – 4 символа.

Таблица 10.7

П

Р

И

М

Е

Р

Э

В

Е

Р

Т

И

К

А

Л

Ь

Н

О

Й

Э

П

Е

Р

Е

С

Т

А

Н

О

В

К

И

2. Записываем группы символов блока исходного текста в строки таблицы перестановок в том порядке, который задает ключ K1 (табл. 10.6). Как видим, в строке номер 5 первые четыре ячейки заняты, а три последние остались свободными.

3. Считываем содержимое табл. 10.6 по столбцам в том порядке, который задан ключом K2 в один блок зашифрованного текста. Этот блок и будет криптограммой:

ЕВРЬРИЕЙТАЭПНРКИНЕВОПЛЕКАРЭАТИМОС.

Перед расшифрованием текст криптограммы разделяют на блоки зашифрованного текста, в каждом из которых R символов. Ключи K1 и K2, а значит, и значения M и N известны. Поэтому для последнего блока зашифрованного текста значение R условия (10.1) выполняются.

Отметим, что при R<M´N число n символов в последней группе исходного текста раскрывает структуру заполнения таблицы перестановок для этой группы: в строке номер M ее левые n ячеек будут заполнены, а остальные N-n ячеек свободны. Значит, и левые n столбцов таблицы будут полными, то есть все их ячейки заполнятся символами. Остальные N-n столбцов будут неполными, их ячейки в строке номер M будут свободны. Величину n вычисляют так:

n=(R)_{mod N}.

При R=M´N окажется, что n=(R)_{mod N}=0,

и все столбцы таблицы перестановок для и последней группы будут полными.

Алгоритм расшифрования блока зашифрованного текста длиною в R символов методом вертикальной перестановки задается такой последовательностью шагов.

0. Создают заготовку таблицы перестановок с номерами строк, заданных ключом K1 и номерами столбцов, заданными ключом K2.

Вычисляют значение n

n=(R)_{mod N},

и определяют структуру заполнения таблицы перестановок. Понятно, что структура заполнения таблицы перестановок для последней группы криптограммы должна получиться такой же, как и структура заполнения таблицы перестановок для последней группы исходного текста.

1. Пользуясь полученной структурой заполнения таблицы перестановок, разбивают блок зашифрованного текста на N групп, номера которых идут в естественном порядке 1, 2,…, N. В каждой группе, которая отвечает полному столбцу в структуре заполнения таблицы перестановок, будет M символов. В каждой группе, которая отвечает неполному столбцу в структуре заполнения таблицы перестановок, будет M-1 символов.

2. В соответствии со структурой заполнения таблицы перестановок заполняют ее, записывая каждую группу символов в свой столбец с номером, который задает ключ K2.

3. Считывают содержимое таблицы перестановок по строкам в том порядке, который задан ключом K1 в один блок расшифрованного текста.

После расшифрования всех блоков зашифрованного текста полученные блоки расшифрованного текста объединяют в один расшифрованный текст.

Пример. Действуя по алгоритму расшифрования, построить и заполнить таблицу перестановок для криптограммы

ЕВРЬРИЕЙТАЭПНРКИНЕВОПЛЕКАРЭАТИМОС.

Убедиться в том, что получим табл. 10.6.

Пример. Расшифровать криптограмму

ШНЕАИОРНОЗТЭОФВЕИЙААПВРКСЕ,

которая получена зашифрованием исходного текста шифром вертикальной перестановки, заданным таблицей перестановок размером 5´6, а также ключами K1=5, 1, 4, 2, 3 и K2=3, 5, 1, 2, 4, 6.

В криптограмме 26 символов, а в таблице перестановок 30 ячеек. Значит, криптограмма представляет собою один блок зашифрованного текста, длина которого R=26 отвечает условиям (10.1): 24<26≤30.

Действуем в соответствии с алгоритмом расшифрования блока зашифрованного текста.

0. Создаем заготовку таблицы перестановок.

Вычисляем

n=(26)_{mod 6}=2,

Таблица 10.8

и определяем структуру заполнения таблицы перестановок. В ней будут заполнены заштрихованные ячейки так: столбцы с номерами 3 и 5 будут полными высотою по 5 ячеек, а остальные столбцы – неполными высотой по 4 ячейки (табл. 10.8).

1. Разбиваем текст криптограммы на группы в соответствии с найденной структурой заполнения таблицы перестановок (табл. 10.9). В группах 1 и 2 будет по четыре символа, в группе 3 – пять, в группе 4 – четыре, в группе 5 – пять, в группе 6 – четыре символа.

Таблица 10.9

Ш

Н

Е

А

И

О

Р

Н

О

З

Т

Э

О

Ф

В

Е

И

Й

А

А

П

В

Р

К

С

Е

2. Записываем каждую группу символов в свой столбец, номер которого задает ключ K1 (табл. 10.9.

Таблица 10.10
	О	Й
	З	А	Ш	И	Ф	Р
	Т	А	Н	О	В	К
	Э	П	Е	Р	Е	С
	О	В	А	Н	И	Е

3. Считываем содержимое табл. 10.10 по строкам в той последовательности, которая задана ключом K2 в блок расшифрованного текста (в котором символ Э заменяем на символ пробела):

ЗАШИФРОВАНИЕ ПЕРЕСТАНОВКОЙ.

10.2. Метод гаммирования

Для шифрования методом гаммирования вся информация (исходный текст, ключ, зашифрованный текст) представляется в числовой форме. Обычно каждому символу буквенного алфавита ставится в соответствие некоторый двоичный код.

Для зашифрования методом гаммирования сначала на основе секретного ключа формируется последовательность двоичных чисел. Каждое число – гамма G_i отвечает своему коду символа исходного текста ТИm_i. Потом над двоичными кодами ТИm_i и G_i выполняют поразрядно операцию сложения по модулю 2. Выполнение этой операции называют наложением гаммы G_i на код ТИm_i (гаммиpованием). Результатом наложения гаммы будет код ТЗm_i символа зашифрованного текста.

Таблица 10.11		Таблица 10.12
x1	x0	Y		Y	x0	x1

Логическая операция сложения по модулю 2 задается табл. 10.11, а записывается как

Y=x₁Åx₀.

Здесь x₁ – цифра кода ТИm_i, x₀ – цифра кода G_i, Y – цифра кода ТЗm_i.

Выбор этой операции для кода гаммирования обусловлен тем, что она обратима (табл. 10.12), то есть

YÅx₀=x₁.

Это делает операцию гаммирования унифицированной: процедура расшифрования криптограммы выполняется путем наложения той же гаммы G_i на тот же код ТЗm_i с получением кода ТИm_i.

Дата добавления: 2014-11-18