Элементы статистической обработки данных 9 страница

Как и всякая математическая наука, теория вероятностей базируется на системе основных понятий. В качестве первого из них назовем понятие случайного эксперимента.

Случайный эксперимент (опыт, испытание, наблюдение) – это реализация той или иной модели случайного явления.

Например, бросание монеты, игрального кубика, операция с колодой карт, стрельба по мишени, оценка состояния преступности в том или ином регионе за определенный срок и др.

Следующее понятие – случайное событие.

Любой из возможных результатов случайного эксперимента называют случайным событием.

Примеры случайных событий:

А – выпадение герба при однократном броске монеты,

В – появление трех решеток при трех последовательных бросках монеты,

С – появление туза при вынимании карты из колоды,

D – поражение мишени при выстреле,

Е – фиксация более 100 преступлений в регионе за сутки.

Различают события составные и элементарные. Например, такое событие как «Сумма очков, выпавших при бросании двух игральных кубиков, равна шести» имеет место, когда результатом бросания будет любая пара чисел:

{(1,5), (2,4), (3,3), (4,2), (5,1)}.

Это перечисление разбивает составное (сложное) событие «Сумма очков равна шести» на пять элементарных событий. Точно так совокупность

{(1,1), (1,3),..., (3,3),..., (5,5)}

суть разложение на элементарные такого сложного события как «Выпали два нечетных числа». Отметим, что элементарное событие {3,3} входит в разложение и первого, и второго из составных событий.

Элементарное событие – это каждый неразложимый исход случайного эксперимента.

Поэтому дальше полагаем, что термины «элементарное событие» и «исход» – синонимы.

Множество всех взаимно исключающих исходов случайного эксперимента называют пространством элементарных событий

и обозначают символом W. Сами элементарные события называют точками пространства W. Исходы называют взаимно исключающими, когда при наступлении одного из них остальные не происходят.

Из сказанного следует, что некоторое событие A представляет собою то или иное подмножество пространства W. Говорят, что событие A наступило, если опыт заканчивается любым из исходов, входящих в состав подмножества A.

Составное событие, которое включает в себя все исходы пространства W, называют достоверным событием, поскольку любой опыт обязательно завершается элементарным событием из множества W. Обозначают достоверное событие тем же символом W.

Для полноты картины в теории вероятностей вводят в рассмотрение и такой результат испытания, в составе которого нет ни одного исхода. Его называют невозможным событием и обозначают как Æ.

Приведем несколько примеров случайных экспериментов, пространств элементарных событий, их подмножеств.

1. Монету бросают два раза подряд (монета – тонкий, однородный круг). Для этого опыта пространство элементарных событий:

W={(Р,Р), (Р,Г), (Г,Р), (Г,Г)},

где Р – выпадение решетки, Г – выпадение герба.

Событие «Выпал хотя бы один герб» – это подмножество {(Р,Г), (Г,Р), (Г,Г)}. Событие «Выпало не более одного герба» – подмножество {(Р,Р), (Р,Г), (Г,Р)}.

2. Бросание игрального кубика (идеального однородного куба). Для этого опыта пространство элементарных событий:

W={1,2,3,4,5,6},

здесь число в скобках – количество выпавших очков.

Событие «Выпало четное число очков» – {2,4,6}. Событие «Выпало менее трех очков» – {1,2}.

Основные операции над событиями. Как видим, события – множества. Поэтому существует и алгебра событий.

Суммой событий A и B называют событие C, которое состоит из всех исходов, входящих или в A, или в B, или в оба эти события сразу.

Обозначают сумму событий так:

C=A+B.

Другими словами, наступление события A+B означает, что произошло хотя бы одно из событий A или B (наступило или A, или B, или оба одновременно).

Произведением событий A и B называют событие C, которое включает в себя все исходы, входящие как в A, так и в B.

Обозначают произведение событий так:

C=A´B.

Иначе, наступление события A´B означает, что события A и B произошли одновременно.

Событием, противоположным для A, называют такое подмножество W, в которое не входит ни один исход, принадлежащий событию A.

Обозначают событие, противоположное для A, как ùA. Наступление события ùA означает, что событие A не произошло.

События A и B называются несовместными, если нет исходов, входящих как в A, так и в B, то есть A´B=Æ.

Другими словами, несовместность событий A и B означает, что они не могут наступить в одном опыте (совместно), что наступление одного из них исключает наступление другого в одном опыте.

События образуют полный набор, если они несовместны, а их сумма есть достоверное событие W.

Например, в урне находятся красные, желтые и синие шары. События «вынут красный шар», «вынут желтый шар», «вынут синий шар» образуют полный набор. Точно так, при бросании игрального кубика события «выпало четное число» и «выпало нечетное число» составляют полный набор. Наряду с термином «полный набор событий» используют термин «полная группа событий».

Приведем примеры из алгебры событий. Бросают игральный кубик. Напомним, что для этого опыта W={1,2,3,4,5,6}. Событие A – выпало четное число, A={2,4,6}, B – выпало число, кратное трем, B={3,6}. Тогда

A+B={2,4,6}+{3,6}={2,3,4,6},

A´B={2,4,6}´{3,6}={6}, ùB={1,2,4,5}.

В алгебре событий имеется своя система тождеств, которые сведены в табл. 7.2. Здесь A, B, C – любые события в данном случайном эксперименте.

Каждое тождество можно (и нужно) выразить словами. Например, тождество 5 читается так: в результате данного опыта любое событие либо происходит, либо нет. Тождество 5’: событие не может одновременно и произойти, и не произойти.

Таблица 7.2
	A+B=B+A			A+B+C=(A+B)+C
1’	A´B=B´A		2’	A´B´C=A´(B´C)
	A+(B´C)=(A+B)´(A+C)			A+Æ=A
3’	A´(B+C)=(A´B)+(A´C)		4’	A´W=A
	A+ùA=W			A+ùA=W
5’	A´ùA=Æ		6’	A´ùA=Æ
	A+A=A			A+(A´B)=A
7’	A´A=A		8’	A´(A+B)=A
	(A´B)+(A´ùB)=A			ù(A+B)=ùA´ùB
9’	(A+B)´(A+ùB)=A		10’	ù(A´B)=ùA+ùB
	ùW=Æ			ùùA=A
11’	ùÆ=W

Как видим, приведенная система тождеств отвечает принципу двойственности. Тождество номер J’ получают из тождества номер J путем замены знака + на знак ´ (или наоборот), символа Æ на символ W (или наоборот). Если утверждение номер J (J= ) верно, то верно и утверждение номер J’ (и наоборот).

Одни из этих тождеств вытекают прямо из определений для операций алгебры событий, другие нужно доказывать. Скажем, утверждение 5 верно, потому, что слагаемое A – некоторое подмножество W, а слагаемое ùA – такое подмножество W, в которое не входят элементы A, и сумма этих подмножеств есть множество W. Докажем, к примеру, утверждение 10. Начнем с его левой части. Событие A+B означает, что наступило или A, или B, или они произошли одновременно. Событие ù(A+B) противоположно описанному, то есть его наступление означает, что не произошло ни A, ни B. Тот факт, что события A и B не случились одновременно, эквивалентен факту, что одновременно произошли противоположные события ùA и ùB, а именно, ùA´ùB. Но это – правая часть утверждения 10. Значит, и в целом оно верно.

7.3. Классическое определение вероятности

Каждое случайное событие обладает той или иной степенью возможности, одно большей, другое меньшей. Для некоторых событий мы можем сразу сказать, какое из них более возможно, а какое менее возможно. Так, событие «выпадение герба при одном броске монеты» более возможно, чем событие «выпадение трех гербов при трех бросках монеты». Относительно других событий аналогичных выводов разу сделать нельзя. Для этого требуется уточнить условия опыта. Так или иначе, ясно, что каждое из случайных событий обладает той или иной степенью возможности. Чтобы количественно характеризовать степень возможности события, нужно с каждым из них связать определенное число, которое тем больше, чем более возможно это событие. Такое число и называют вероятностью события.

Итак, вероятность случайного события представляет собою количественную меру возможности его наступления.

Классический метод вычисления вероятностей сформировался в XVII веке как результат анализа азартных игр. В основе классического определения вероятности лежит понятие равновозможности исходов случайного эксперимента.

Равновозможность исходов означает, что нет никаких оснований предпочесть один исход другим, все исходы из рассматриваемого пространства элементарных событий имеют равные вероятности. Например, появление герба или решетки при одном броске монеты – исходы равновозможные. Чаще всего вывод о равновозможности исходов основан на соображениях о симметрии и однородности объектов, над которыми производится случайный эксперимент (каждая монета – тонкий, однородный круг, а каждый игральный кубик – идеальный однородный куб).

Рассмотрим испытание, в результате которого может наступить событие A. Каждый исход, принадлежащий подмножеству A, называют благоприятным событию A. Пусть, например, событие A – выпадение нечетного числа очков при одном броске игрального кубика. Понятно, что из шести равновозможных исходов этого эксперимента {1,2,3,4,5,6} благоприятными событию A являются три: {1,3,5}.

Теперь можно дать классическое определение вероятности.

Вероятностью события A называется отношение числа исходов, благоприятных событию A, к числу всех возможных исходов испытания.

Вероятность события A обозначают как P(A), число исходов, благоприятных A, как m(A), число всех возможных исходов как m(W)=n. Тогда по определению

P(A)= 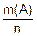. (7.9)

Например, для вычисления вероятности события «выпадение нечетного числа очков при одном броске игрального кубика» имеем: m(A)=3, n=6. Значит,

P(A)= = .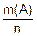

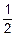Из определения вероятности вытекают следующие ее свойства.

1. Вероятность достоверного события равна единице. Действительно, число исходов, благоприятных достоверному событию W, равно мощности пространства элементарных событий m(W)=n. Значит, по формуле (7.9) имеем

P(W)= =1.

2. Вероятность невозможного события равна нулю. В самом деле, для события Æ в пространстве элементарных событий нет ни одного благоприятного, то есть m(Æ)=0, и

P(Æ)= 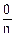=0.

3. Вероятность произвольного случайного события заключена между нулем и единицей. Действительно, число исходов, благоприятных случайному событию A, находится в пределах 0£m(A)£n. Разделив каждый операнд в этих неравенствах на n, получим

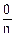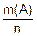£ £ , или 0£P(A)£1.

4. Вероятность события ùA, противоположного событию A, вычисляется так:

P(ùA)=1-P(A). (7.10)

Число исходов, благоприятных событию A, равно m(A) из n. Остальные n-m(A) исходов благоприятны противоположному событию, поскольку события A и ùA несовместны и образуют полный набор: A´ùA=Æ, и m(A´ùA)=0. Значит, по определению вероятность события ùA есть

P(ùA)= =1-P(A).

5. Вероятность суммы произвольных событий A+B вычисляется так:

P(A+B)=P(A)+P(B)-P(A´B). (7.11)

Когда A´B¹Æ, в составе события A имеется m(A´B) исходов, относящихся к событию A´B. Столько же таких исходов имеется и в составе события B. Поэтому сумма m(A)+m(B) включает в себя слагаемое m(A´B) дважды. Но в состав события A+B каждый из исходов, относящихся к событию A´B, должен входить лишь один раз. Поэтому число m(A+B) содержит в себе только одно число m(A´B), а не два. Значит,

m(A+B)=m(A)+m(B)-m(A´B).

Отсюда по определению получаем формулу (7.11), которую называют формулой (теоремой) сложения вероятностей.

Вероятность суммы несовместных событий A+B равна

P(A+B)=P(A)+P(B). (7.12)

Если события A и B несовместны, то A´B=Æ, и m(A´B)=0. Значит, P(A´B)=0, и формула (7.11) преобразуется к формуле (7.12).

Правило (7.12) по индукции распространяется на произвольное число попарно несовместных событий A_k, k= :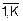

.

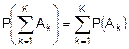Попарно несовместные события A_i и A_j – это те события, для которыхвыполняется условие A_i´A_j=Æ при любых i¹j, i,j= .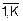

Пусть события A, B,..., C образуют полный набор. Тогда

P(A)+P(B)+¼+P(C)=1.

В самом деле, по определению A+B+¼+C=W, а P(W)=1.

7.4. Теорема умножения вероятностей

Введем сначала важные понятия о событиях независимых и зависимых.

Событие B называется независимым от события A, если вероятность наступления B не изменяется от того, произошло A или нет.

Событие D называется зависимым от события C, если вероятность наступления D имеет одно значение, когда C не произошло, и эта вероятность имеет другое значение тогда, когда C наступило.

Факт независимости случайных событий устанавливают путем анализа условий задачи, исследования модели случайного эксперимента.

Пример. Рассмотрим два случайных эксперимента.

1. В урне два белых шара и один черный. Из урны наугад вынимают один шар, фиксируют его цвет и возвращают шар в урну. Рассматриваются два события:

Б1 – появление белого шара в первой попытке,

Б2 – появление белого шара во второй попытке.

Очевидно, что вероятность наступления события Б2 равна 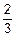, и она никак не зависит от того, произошло событие Б1, или оно не произошло. Значит, в этом случайном эксперименте событие Б2 не зависит от события Б1.

2. В урне два белых шара и один черный. Из урны наугад вынимают один шар, но не возвращают его в урну. Изучаются два события:

Б1 – появление белого шара в первой попытке,

Б2 – появление белого шара во второй попытке.

Теперь вероятность наступления события Б2 существенно зависит от того, имело место событие Б1 или нет. Если событие Б1 (вероятность его наступления равна 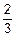) произошло, то вероятность наступления Б2 равна 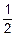(в урне остались один белый шар и один черный). Если же событие Б1 не наступило, то вероятность события Б2 равна 1 (в урне осталось только два белых шара). Значит, в этом случайном эксперименте событие Б2 зависит от события Б1.

Вероятность события B, вычисленная при условии, что имело место событие A, называется условной вероятностью события B и обозначается как P(BïA).

Сформулируем теорему умножения вероятностей.

Вероятность произведения событий A´B равна произведению вероятности первого сомножителя на условную вероятность второго сомножителя, вычисленную при условии, что первое событие имело место:

P(A´B)=P(A)´P(B½A). (7.13)

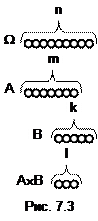Пусть в пространстве W (рис. 7.3) насчитывается n исходов. Событию A благоприятны m исходов, событию B благоприятны k исходов. Среди исходов, благоприятных событию A существуют исходы, которые благоприятны и событию B. Это те же l исходов, которые благоприятны событию A´B (рис. 7.3). Тогда P(A)= , P(A´B)= .

Условную вероятность P(B½A) вычисляем, исходя из того факта, что событие A наступило. И если A наступило, то исходы, благоприятные событию B нужно выбирать из m исходов, составляющих событие A. Как видим (рис. 7.3), имеется l таких исходов. Значит, условная вероятность P(B½A) вычисляется так:

P(B½A)= .

Подставив полученные выражения для P(A´B), P(A) и P(B½A) в формулу (7.13), получим тождество. Это означает, что теорема умножения вероятностей доказана.

Методом математической индукции теорему умножения вероятностей можно распространить на произведение любого числа событий:

P(A´B´C)=P(A)´P(B½A)´P(C½(A´B)),

P(A´B´C´D)=

=P(A)´P(B½A)´P(C½(A´B))´P(D½(A´B´C)) и т.д.

Пример. В урне лежат три белых, три черных и три желтых шара. Наугад вынимают один за другим три шара. Какова вероятность того, что все три вынутых шара окажутся одного цвета?

Первый шар может быть любого цвета – событие Ц1 (и это событие – достоверное). Но второй шар должен быть того же цвета, что и первый – событие Ц2. Третий шар должен быть того же цвета, что и два первых – событие Ц3. Событие Ц, состоящее в том, что все три шара одновременно окажутся одного цвета суть произведение трех названных: Ц=Ц1´Ц2´Ц3. Далее по условию задачи: P(Ц1)=1, P(Ц2½Ц1)= 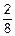, а P(Ц3½(Ц1´Ц2))= 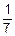. Поэтому

P(Ц)=P(Ц1)´P(Ц2½Ц1)´P(Ц3½(Ц1´Ц2))=1´ ´ = .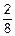

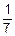Следствием из теоремы умножения вероятностей будет такое утверждение.

Если событие B не зависит от события A, то и событие A не зависит от события B.

Условие независимости события A (события B) от события B (от события A) записывается так:

P(BïA)=P(B), (7.14)

P(AïB)=P(A). (7.15)

Положим, что (7.14) дано (событие B не зависит от события A) и докажем утверждение (7.15) – событие A не зависит от события B.

Запишем формулу умножения вероятностей для событий B´A и A´B:

P(B´A)=P(B)´P(A½B),

P(A´B)=P(A)´P(B½A).

В силу тождества 1’ алгебры событий (табл. 7.2) левые части этих выражений равны. Значит, равны и их правые части:

P(B)´P(A½B)=P(A)´P(B½A),

или, согласно (7.14)

P(B)´P(A½B)=P(A)´P(B).

Полагая, что P(B)¹0, разделим обе части этого равенства на P(B):

P(A½B)=P(A),

что и требовалось доказать.

Для независимых событий теорема умножения вероятностей звучит так.

Вероятность произведения независимых событий равна произведению вероятностей этих событий:

P(A´B)=P(A)´P(B),

P(A´B´C)=P(A)´P(B)´P(C),

P(A´B´C´D)=P(A)´P(B)´P(C)´P(D) и т.д.

Пример. Вероятность того, что студент Имярек сдаст экзамен по ГП (гражданскому праву) P(ГП)=0.7, а вероятность сдачи им экзамена по СС (судебной статистике) P(СС)=0.8. Найти вероятность того, что Имярек а) сдаст оба экзамена, б) оба экзамена не сдаст.

а) Событие «сданы оба экзамена» суть ГП´СС. События ГП и СС физически независимы. Поэтому

P(ГП´СС)=P(ГП)´P(СС)=0.7´0.8=0.56.

б) Если события ГП и СС независимы, то независимы и противоположные события ùГП и ùСС. Вероятности этих событий вычисляются по формуле (7.10):

P(ùГП)=1-P(ГП)=0.3, P(ùСС)=1-P(СС)=0.2.

Событие «оба экзамена не сданы» – это ùГП´ùСС. Значит,

P(ùГП´ùСС)=(1-P(ГП))´(1-P(СС))=0.3´0.2=0.06.

7.5. Основные формулы теории вероятностей

Формула полной вероятности. Данная формула вытекает из законов сложения и умножения вероятностей. Пусть некоторое событие A может произойти совместно с одним из событий H₁, H₂,…, H_n, образующих полную группу. Эти события называют гипотезами, потому что A происходит в том предположении, что случилось хотя бы одно из этих событий:

A=H₁´A+H₂´A+¼+H_n´A.

Поскольку гипотезы H₁, H₂,…, H_n образуют полный набор, они попарно несовместны. Поэтому и события H₁´A, H₂´A, ¼, H_n´A попарно несовместны. Значит, к вычислению вероятности P(A) можно применить формулу сложения вероятностей (7.12):

P(A)=P(H₁´A)+P(H₂´A)+¼+P(H_n´A)= .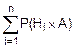

А вероятность P(H_i´A) произведения событий H_i´A вычисляется по формуле (7.13):

P(H_i´A)=P(H_i)´P(A½H_i).

Тогда

P(A)=P(H₁)´P(A½H₁)+P(H₂)´P(A½H₂)+¼+P(H_n)´P(A½H_n)=

= P(A½H_i), (7.16)

то есть вероятность события A вычисляется как сумма произведений вероятности каждой гипотезы на условную вероятность события A при этой гипотезе. Формула (7.16) и носит название формулы полной вероятности.

Пример. В цехе две группы станков производят одни и те же детали, которые в произвольном порядке отправляются на склад. Станков первой группы 4, и они дают 5% брака. Станков второй группы 6, и брака у них 10%. Найти вероятность того, что наугад взятая со склада деталь окажется бракованной.

Событие A – деталь бракованная. Возможны следующие гипотезы для наступления этого события:

H₁ – деталь изготовлена на станках первой группы, и вероятность этой гипотезы P(H₁)= =0.4;

H₂ – деталь изготовлена на станках второй группы, и вероятность этой гипотезы P(H₂)= =0.6.

Гипотезы образуют полную группу событий.

Далее, событие A½H_i (i= ) – бракованная деталь была изготовлена на станках i-й группы. Вероятность этого события связана с процентом брака на станках i-й группы: P(A½H₁)=0.05, P(A½H₂)=0.10. Очевидно, что событие A произошло, если имело место или событие A½H₁, или событие A½H₂, то есть A=A½H₁+A½H₂. Значит,

P(A)=P(H₁)´P(A½H₁)+P(H₂)´P(A½H₂)=

=0.4´0.05+0.6´0.10=0.08.

Формула Байеса. Сначала вернемся к только что рассмотренному примеру и дополним его так. Пусть событие A наступило, наугад отобранная деталь оказалась бракованной. Спрашивается, какова вероятность того, что эта деталь изготовлена на станках i-й группы, то есть реализовалась гипотеза H_i?

Понятно, что в нашем случае событие A происходит одновременно с событием H_i, то есть имеет место событие H_i´A или, что то же самое, A´H_i. По формуле (7.13) для этих событий имеем:

P(H_i´A)=P(H_i)´P(A½H_i),

P(A´H_i)=P(A)´P(H_i½A).

Левые части этих выражений равны, равны и их правые части:

P(H_i)´P(A½H_i)=P(A)´P(H_i½A).

Отсюда

P(H_i½A)= . (7.17)

Напомним, что здесь i= . Величины, входящие в формулу (7.17), нами уже определены: P(H₁)=0.4, P(H₂)= 0.6, P(A½H₁)=0.05, P(A½H₂)=0.10, P(A)=0.08. Тогда

P(H₁½A)=0.25, P(H_i½A)=0.75.

Если знаменатель в выражении (7.17) вычислить по формуле (7.16), получим формулу Байеса для двух гипотез (i= ):

P(H_i½A)= .

В общем случае для i= она записывается так:

P(H_i½A)= 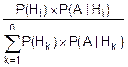. (7.18)

Формула Байеса (или формула гипотез) позволяет пересчитать вероятности каждой из гипотез после того, как наступило обусловленное ими событие. В формуле (7.18) исходные вероятности гипотез P(H_i) называются априорными (доопытными), а искомые вероятности P(H_i½A) – апостериорными (послеопытными).

Пример. Два охотника одновременно и независимо стреляют в кабана. Известно, что первый попадает в цель с вероятностью 0.8, а второй – с вероятностью 0.5. Кабан убит, и в нем обнаружена одна пуля. Как справедливо разделить трофей?

Здесь событие A – наличие в убитом кабане одной пули после такого испытания, как два одновременных и независимых выстрела. В качестве гипотез выступают возможные результаты этого испытания:

H₀₀ – не попал ни первый стрелок, ни второй,

H₁₀ – попал первый, не попал второй,

H₀₁ – не попал первый, попал второй,

H₁₁ – попал и первый, и второй.

Обозначим элементарные события в данном испытании: F – попал первый, T – попал второй. Их вероятности заданы:

Дата добавления: 2014-11-18