Элементы статистической обработки данных 8 страница

Напомним, что величина C´h²=F-F_h характеризует погрешность формулы трапеций (6.2). Значит,

F-F_h= 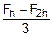=PR. (6.7)

Как видим, теперь в оценке погрешности интегрирования по формуле трапеций (6.2) нет нужды оперировать с неопределенной величиной C (см. формулу (6.3)), а использовать для этих целей текущее значение PR.

Итак, если вычисление определенного интеграла от заданной функции f(x) на заданном отрезке [a,b] по формуле Ньютона-Лейбница дает точный результат F_NL, то результат, полученный по формуле трапеций F_h, имеет в соответствии с (6.7) погрешность ïF_NL-F_hï=ïPRï.

Очевидно, что результат F_RR, полученный по методу Рунге-Ромберга должен отвечать неравенству

ïF_NL-F_RRï<ïPRï.

По окончании вычислений следует проверить это неравенство с тем, чтобы убедиться в верности полученных результатов.

Опишем процедуру вычисления определенного интеграла от таблично заданной функции {xt_i,yt_i} по формуле трапеций методом Рунге-Ромберга. Остановимся на том случае, когда таблица {xt_i,yt_i} составлена по результатам эксперимента. Значит, шаг такой таблицы уменьшить нельзя. Однако и от такой таблицы можно вычислить определенный интеграл с более высокой точностью, чем та, которую дает для нее формула трапеций (6.2). Делается это так. Сначала по формуле (6.2) вычисляют величину F_h, используя все отсчеты таблицы yt₀,yt₁,yt₂,...,yt_n, расстояние между которыми равно h. А затем вычисляют величину F_2h, используя только 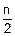отсчетов таблицы yt₀,yt₂,...,yt_n c четными номерами, расстояние между которыми равно 2´h. Имея значения F_h и F_2h, по формуле (6.5) вычисляют поправку Рунге PR, а потом по формуле (6.6) искомое значение определенного интеграла F_RR по методу Рунге-Ромберга, которое точнее чем F_h.

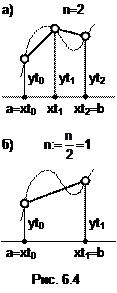Для вычисления определенного интеграла методом Рунге-Ромберга объем n исходной таблицы {xt_i,yt_i} должен быть кратным степени двойки (см. (6.4)). Его минимальное значение n=2 (рис. 6.4,а). Действительно, при таком объеме исходной таблицы на втором этапе вычислений (рис. 6.4,б) получим 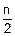=1, и величина F_2h вычисляется как площадь одной трапеции, у которой основаниями будут только два крайних отсчета таблицы yt₀ и yt₁, а высота – суть 2´h=xt₁-xt₀=b-a. Поэтому формулу (6.2) для метода Рунге-Ромберга следует преобразовать так:

F_h= 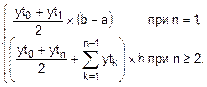. (6.8)

На рис.6.5 показан граф алгоритма для вычисления определенного интеграла от таблично заданной функции по формуле трапеций методом Рунге-Ромберга. Здесь рис. 6.5,а описывает сам метод Рунге-Ромберга, а рис. 6.5,б задает вычисления по формуле трапеций (6.8). В блоке 0 (рис. 6.5,а) задаем табличную функцию {xt_i,yt_i}, ее объем n и шаг h. В блоке 1 из всех отсчетов {yt_i} табличной функции образуют массив Y. В блоке 2 происходит обращение к формуле трапеций (рис.6.5,б) с данными Y, n, h. Результатом будет значение F_h определенного интеграла на шаге h. В блоке 3 из отсчетов табличной функции с четными номерами формируем массив Y2, в котором эти отсчеты табличной функции получают новую сплошную нумерацию 0, 1, 2,..., 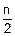. В блоке 4 массиву Y2 придаем имя Y, значение n уменьшаем, а шаг h увеличиваем вдвое. В боке 5 с этими новыми данными Y, n, h опять обращаемся к формуле трапеций (рис.6.5,б) и получаем величину F_2h, а именно, значение определенного интеграла на шаге 2´h. В блоке 6 вычисляется поправка Рунге PR. Наконец, в блоке 7 получаем искомое значение F_RR определенного интеграла по формуле Рунге-Ромберга.

Пример. Выполним ручную прокрутку алгоритма (рис.6.5). В табл. 6.2 приведены данные о количестве преступлений в РФ за три года. Вычислить среднее количество преступлений за этот период.

Таблица 6.2
Зарегистрировано преступлений (тыс.)
i
Гтi
Птi	3554.7	3855.4	3582.5
j

Действуем по рис.6.5,а, предварительно выполнив замену обозначений для операндов: xt_i, yt_i на Гт_i и Пт_i, Y, Y2 на П и П2, соответственно

0. Таблица {Гт_i,Пт_i} задана (табл. 6.2), объем n=2, шаг h=1.

1: П={3554.7, 3855.4, 3582.5}.

2: F_h= = .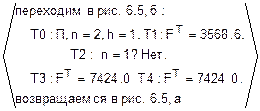

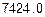3: П2={3554.7, 3582.5}.

4: Y=Y2, n=1, h=2.

5: F_2h= = .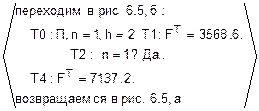

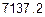6: PR=95.6.

7: F_RR=7519.6.

Теперь вычислим среднее количество преступлений П_ср за период DГ=2007-2005=2 года.

П_ср= 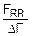= =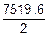3759.8.

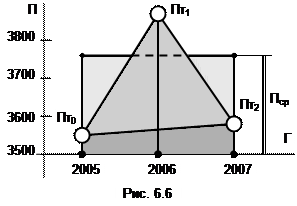
На рис. 6.6 представлены исходные данные и результаты решения задачи. Cветлыми кружками отмечены отсчеты табличной функции Пт_i, черными точками на оси абсцисс – значения Гт_i. На первом плане темной заливкой выделена трапеция площадью F_2h. На втором плане более светлой заливкой показаны две трапеции общей площадью F_h (их нижние части не видны). На заднем плане виден самый светлый прямоугольник площадью F_RR. Его высота равна искомой величине П_ср, а основание DГ=2007-2005.

Вопросы и задачи для самоконтроля

1. Сформулировать понятие определенного интеграла. Пояснить процедуру вычисления определенного интеграла по формуле Ньютона-Лейбница.

2. Определить понятие первообразной и неопределенного интеграла.

3. Перечислить свойства интегралов.

4. Записать таблицу интегралов.

5. Вычислить первообразные:

а) F(x)= 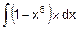, б) F(x)= ,

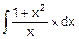в) F(x)= .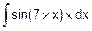

6. Вычислить площадь плоской фигуры, ограниченной параболой y=x²+1, на отрезке от a=-3 до b=3.

7. Пояснить правила вычисления определенных интегралов методом замены переменной и по частям. Вычислить определенные интегралы:

а) F= 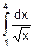, б) F= 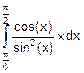, в) F= .

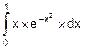8. Пояснить, что такое несобственный интеграл. Вычислить

а) F= 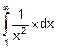, б) F= .

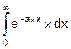9. Пояснить процедуру вывода формулы трапеций и смысл метода Рунге-Ромберга для вычисления определенных интегралов.

10. Вычислить 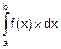для f(x)=e^-x, a=-1.0, b=3.0

а) по формуле Ньютона-Лейбница,

б) методом Рунге-Ромберга по формуле трапеций.

11. Выполнить ДКЗ: Тест 6. ОСНОВЫ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ.

Эксцессом исполнителя признается совершение исполнителем преступления, не охватывающегося умыслом других соучастников. За эксцесс исполнителя другие соучастники преступления уголовной ответственности не подлежат.

(УК РФ, Ст. 36)

РАЗДЕЛ III
ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ

Глава 7. ПОНЯТИЕ ВЕРОЯТНОСТИ

7.1. Элементы комбинаторики

Комбинаторика – это область математики, где решаются задачи определения числа комбинаций, которые можно составить по тем или иным правилам из заданного количества объектов.

Правило умножения. Начнем с примера. В ОВД служат три следователя С₁, С₂, С₃, два оперативника О₁, О₂ и три эксперта Э₁, Э₂, Э₃. Для выезда на место происшествия всякий раз отправляют группу из трех человек: следователя, оперативника и эксперта. График работы групп составляется так, чтобы каждая следующая группа отличалась от предыдущей. Сколько дней это условие будет выполняться?

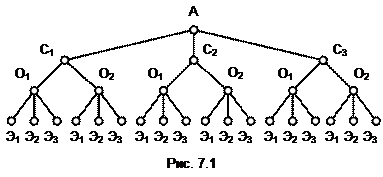
Понятно, что группы составляются с учетом того, что следователя в нее можно выбирать тремя способами, оперативника – двумя, эксперта – тремя. Составим такую схему (рис. 7.1). Здесь отрезки АС₁, АС₂, AС₃ отображают варианты назначения в группу следователя. Отрезки С₁О₁, С₁О₂, С₂О₁, С₂О₂, С₃О₁, С₃О₂ показывают, кто из оперативников с каким следователем включен в группу. Наконец, отрезки из точек О₁ и О₂ в точки Э₁, Э₂, Э₃ указывают, какой из экспертов включается в группу. Всякий путь из точки А к какой-либо из точек Э₁, Э₂, Э₃ отображает состав одной из групп. Например, путь АС₂О₁Э₃ отвечает группе, в которую включены следователь С₂, оперативник О₁ и эксперт Э₃. Общее количество различных групп легко найти, перемножив число отрезков, выходящих из точки А на число отрезков с началами в точках С₁, С₂, С₃ и на количество отрезков, проведенных из точек Э₁, Э₂, Э₃: 3´2´3=18. Если группа дежурит сутки, то через 18 дней группы начнут повторяться.

Этот пример иллюстрирует применение для решения комбинаторных задач правила умножения. В общем случае оно формулируется так.

Пусть требуется выполнить одно за другим n действий: И действие Д1, И действие Д2, И ¼, И действие Дn. При этом действие Д1 может быть выполнено m₁ способами, действие Д2 – m₂ способами и т. д., наконец, действие Дn выполняется m_n способами. Тогда общее число S_n всех способов, которыми можно выполнить все n действий, вычисляется так:

S_n=m₁´m₂´¼´m_n. (7.1)

Доказательство этого утверждения проведем методом математической индукции, который является одним из самых универсальных методов доказательства математических теорем. Суть его состоит в следующем. Допустим, мы хотим доказать, что некоторое утверждение справедливо для любого натурального n, содержащегося в формулировке этого утверждения. Для этого достаточно:

проверить верность утверждения для n=1;

предположив, что оно верно для n=k, доказать, что оно верно и для n=k+1.

В нашем случае при n=1 имеем одно действие, которое выполняется m₁ способами, и

S₁=m₁.

Допустим, что утверждение (7.1) верно для n=k действий

S_k=m₁´m₂´¼´m_k.

Докажем, что оно верно и для n=k+1 действий. Обозначим каждый конкретный вариант выполнения всех k действий набором из k чисел. Например, набор

(3₁, 1₂,..., 5_k)

указывает на тот вариант выполнения всех k действий, когда первое действие выполнено третьим способом (из m₁ способов), второе – первым способом (из m₂ способов), и т. д., а k-е действие – пятым (из m_k способов). Добавим к имеющимся k действиям еще одно – (k+1)-е. Тогда любой из вариантов выполнения всех k+1 действий можно задать набором из k+1 чисел. При этом в наборе для данного варианта первые k чисел остаются прежними, а последнее число принадлежит интервалу от 1 до m_k+1. Таким образом, каждому варианту выполнения k действий отвечает m_k+1 вариантов выполнения k+1 действий, например,

(3₁, 1₂,..., 5_k, 1_k+1),

(3₁, 1₂,..., 5_k, 2_k+1),

¼

(3₁, 1₂,..., 5_k, m_k+1).

Значит, общее число S_k+1 всех способов выполнения k+1 действий будет равно

S_k+1=S_k´m_k+1=m₁´m₂´¼´m_k´m_k+1.

Итак, утверждение (7.1) верно для любого натурального n.

В первом примере формирование групп для выезда на место происшествия выполнялось k=3 действиями:

первое – выбор следователя, m₁=3,

второе – выбор оперативника, m₂=2,

третье – выбор эксперта, m₃=3.

При этом S₃=18. Добавим в состав группы водителя, которых в ОВД двое. Теперь при формировании групп придется выполнять и четвертое действие двумя способами (m₄=2), и S₄=S₃´m₄=36.

Еще одна комбинаторная задача. Имеем q символов, а количество экземпляров каждого символа неограниченно. Сколько вариантов заполнить этими символами k позиций? В первую позицию можно записать любой из q символов, во вторую тоже любой из q символов и так далее, наконец, в позицию номер k можно записать тоже q символов. По правилу умножения получаем цепочку из k одинаковых сомножителей q, то есть:

N_q,k=q^k.

Пример. В жюри 11 человек. Каждый может высказаться за, против или воздержаться. Сколько вариантов решений может быть принято этим жюри?

Решение. Здесь символы – высказывания членов жюри и q=3, а сами они – позиции и k=11. Значит, N_3,11=3¹¹=177147.

Рассмотрим и такую комбинаторную задачу. Имеем r множеств D_j мощностью n_j каждое (j= 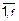). Из элементов этих множеств составляют комбинации такие, что в данную комбинацию включается только один элемент из каждого множества. Тогда общее число K_r различных комбинаций такого рода равно

K_r=n₁´n₂´¼n_r. (7.2)

Представим себе такую картину. Каждую комбинацию набирают в строке из r ячеек, а каждая ячейка номер j этой строки заполняется только элементом из множества D_j (j= 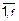). Первая ячейка может быть заполнена любым из n₁ элементов множества D₁, вторая – любым из n₂ элементов множества D₂ и т. д., последняя r-я ячейка – любым из n_r элементов множества D_r. По правилу умножения и получим для общего количества комбинаций K_r формулу (7.2).

И снова пример. Из отличников первого курса РАП составляют команду для участия в городской олимпиаде по информационным технологиям. В команду входит по одному отличнику из трех групп. Сколько вариантов команд можно составить, если в первой группе 6 отличников, во второй – 4 и в третьей – 5.

Решение. Здесь D₁ – отличники первой группы (n₁=6), D₂ – отличники второй (n₂=4), D₃ – отличники третьей группы (n₃=5). Значит, K₃=6´4´5=120.

Правило сложения. Еще пример. Из отличников первого курса РАП нужно выбрать одного. Сколькими способами можно решить эту задачу?

Выбрать одного отличника из первой группы можно n₁=6 способами, из второй – n₂=4 способами, из третьей – n₃=5 способами. Отличник выбирается ИЛИ из первой группы, ИЛИ из второй, ИЛИ из третьей. При этом один выбор исключает остальные. Поэтому общее количество способов выбрать одного отличника равно n₁+n₂+n₃=15.

Этот пример позволяет сформулировать правило сложения.

Имеем j действий, первое из которых реализуется m₁ способами, второе – m₂ способами и т.д., наконец, j-е действие выполняется m_j способами. Выполняется только одно из них: ИЛИ первое, ИЛИ второе, ИЛИ ¼ ИЛИ j-е. Это одно действие можно выполнить C_j способами:

C_j=m₁+m₂+¼+m_j.

Перестановки, размещения, сочетания. При решении комбинаторных задач имеют дело с комбинациями из некоторых элементов. Эти комбинации могут отличаться одна от другой числом элементов, их составом или порядком. Пусть задано множество из n элементов и строка из k ячеек. Пронумеруем ячейки от 1 до k.

Перестановкой называют то или иное распределение n элементов в строке из k=n ячеек.

Общее число всех различных перестановок из n элементов обозначают как P_n и вычисляют так:

P_n=n!. (7.3)

Действительно, всякую перестановку можно получить с помощью n действий: первое действие – выбор элемента в первую ячейку строки, второе – выбор элемента во вторую ячейку и т. д., наконец, последнее n-е действие – заполнение последней ячейки строки. Первое действие можно выполнить n способами, а именно, поместить в первую ячейку любой из n элементов. Вторую ячейку заполняют любым из оставшихся n-1 элементов, то есть n-1 способами. Каждая следующая ячейка может быть заполнена числом способов на единицу меньше, чем предыдущая. Последняя ячейка заполняется единственным способом – последним элементом. Значит, по правилу умножения

P_n=n´(n-1)´¼´1=n!.

Напомним, что записью n! обозначают факториал, что (n+1)!=n!´(n+1), что 0!=1.

Пример. Общее число лиц, предъявляемых для опознания, должно быть не менее трех. Перед началом опознания опознаваемому предлагается занять любое место среди предъявляемых лиц (УПК, ст.193, ч.4). Сколько вариантов у опознаваемого занять любое место среди трех предъявляемых лиц, среди четырех?

Решение. Здесь всякий вариант предъявления для опознания n лиц – перестановка P_n из n={4,5}. Значит,

P₄=4´3´2´1=24, а P₅=P₄´5=120.

Размещением из n элементов по k называется то или иное распределение n элементов в строке из k ячеек.

Другими словами, размещение из n элементов по k получают так: каким-либо способом из заданных n элементов выбирают k и, так или иначе, распределяют их в k же ячейках.

Общее число всех размещений из n элементов по k обозначают как 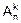и вычисляют по формуле

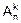=n´(n-1)´¼´(n-k+1). (7.4)

Это утверждение доказывается так же, как и формула (7.3). Каждое размещение получается с помощью k действий. Первое действие – выбор элемента для заполнения первой ячейки строки. Оно реализуется n способами. Второе действие – заполнение второй ячейки реализуется n-1 способами. Последнее действие – заполнение последней k-й ячейки реализуется n-k+1 способами. По правилу умножения и получаем формулу (7.4) для 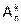. Иногда ее удобно представить так:

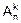=n´(n-1)´¼´(n-k+1)= 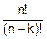= 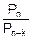. (7.5)

Пример. Очевидец транспортного происшествия запомнил лишь то, что все три цифры номера машины нарушителя были разными, а первой цифрой была 4. Сколько машин должна будет проверить автоинспекция?

Второй и третьей цифрами номера могут быть любые две из множества {0, 1, 2, 3, 5, 6, 7, 8, 9}. Выбрав любую пару цифр, получают номер какого-то автомобиля. Так, пара {5, 7} дает номер 457, а пара {7,5} – номер 475. Значит, нужно перебрать все перестановки из девяти цифр по две. Поэтому придется проверить

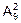=9´8=72 машины.

Сочетанием из n элементов по k называется всякая неупорядоченная совокупность k элементов, каким-либо способом выбранная из данных n элементов.

Общее число всех сочетаний из n элементов по k обозначают как 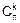, а вычисляют так:

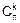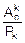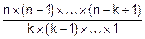= = . (7.6)

По определению в одном сочетании из n элементов по k выборка из k элементов неупорядочена. Если же эту одну выборку начать упорядочивать (распределять k ее элементов по k ячейкам строки), то из каждого сочетания получим P_k перестановок. А всего таких перестановок будет 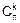, то есть

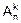=P_k´ .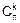

Отсюда и следует формула (7.6). Она означает, что 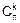в P_k раз меньше 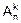. Выражение (7.6) с учетом формулы (7.5) можно преобразовать к такому виду:

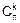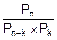= . (7.7)

Пример. Для участия в процедуре опознания из восьми подходящих сотрудников ОВД всякий раз выбирают троих. Сколько различных троек можно составить из этих восьми сотрудников?

Каждая тройка отобранных сотрудников никак не упорядочена, то есть представляет собою сочетание из n=8 по k=3. Всего же таких сочетаний будет

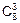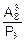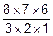= = =56.

Укажем на некоторые свойства сочетаний.

1. 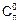=1.

Это свойство следует из того факта, что по определению 0!=1.

2. 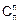=1.

Это свойство легко подтверждается непосредственной подстановкой в (7.6) k=n.

3. = .

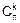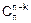Это свойство прямо следует из формулы (7.7):

= = = =

= = .

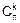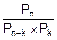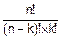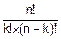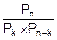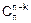При k> 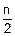оказывается, что n-k<k, и 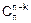вычислить проще чем .

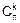7.2. Случайные события

Окружающий нас мир полон таких явлений, которые имеют случайный характер. Например, производится стрельба из орудия, установленного под углом к горизонту (рис. 7.2). Теоретически траектория снаряда представляет собою параболу

y_Т(x)=a´x²+b´x+c, (7.8)

и все выпущенные снаряды должны попадать в одну и ту же точку Ц. Однако практика показывает, что при каждом новом выстреле фактическая траектория очередного снаряда неизбежно отличается от y_Т(x). Обусловлено это влиянием многих факторов (порывами ветра, различиями в весах зарядов и др.). Эти факторы при выводе формулы (7.8) не учитываются, да и вряд ли могут быть учтены.

Итак, случайное явление при многократном воспроизведении протекает всякий раз по-новому. Элементы неопределенности, сложности, многопричинности, присущие случайным явлениям, требуют специальных методов для изучения этих явлений. Такие методы и разрабатываются в теории вероятностей. Предметом теории вероятностей являются специфические закономерности, которые наблюдаются в случайных явлениях.

Практика показывает, что в большой массе однородных случайных явлений обнаруживаются вполне определенные закономерности, свойственные именно массовым случайным явлениям. Например, при ограниченном числе выстрелов (рис. 7.2) точки разрыва снарядов относительно точки Ц расположены в полном беспорядке, без какой-либо видимой закономерности. По мере увеличения числа выстрелов в расположении точек разрыва наблюдается устойчивая закономерность: густота разрывов по мере удаления от точки Ц убывает по вполне определенному закону, который называется нормальным.

Следует особо подчеркнуть, что методы теории вероятностей по природе своей приспособлены только для исследования массовых случайных явлений. Они не дают возможности предсказать, к чему приведет отдельное случайное явление, но дают возможность предсказать средний суммарный результат массы однородных случайных явлений. Например, интуиция подсказывает, а практика подтверждает, что при большом числе бросаний монеты герб выпадает в половине бросков (первые две строки в табл. 7.1). Если же сделать несколько бросков, этой закономерности не видно (две последние строки в табл. 7.1).

Таблица 7.1
Экспериментатор	Число бросаний	Число гербов
Бюффон
Пирсон
Королев
Радионов

Во всех случаях, когда применяются вероятностные методы, их цель в том, чтобы, минуя слишком сложное (а зачастую и невозможное) описание отдельного явления, обратиться прямо к законам, которые управляют массами случайных явлений. Эти законы позволяют не только осуществить научный прогноз в заданной области случайных явлений, но в ряде случаев целенаправленно влиять на их ход, ограничивать сферу действия случайности.

Подобно другим отраслям математики, теория вероятностей родилась и развивалась из потребностей практики. Уже в XVII веке были предприняты первые попытки создания общей теории страхования, основанной на анализе закономерностей таких массовых случайных явлений как заболеваемость, смертность людей, несчастные случаи с ними и др. Но как отрасль математики теория вероятностей сформировалась отнюдь не на материалах такого рода практических задач. Эти задачи чрезвычайно сложны, закономерности, управляющие случайными явлениями в них, проявляются недостаточно отчетливо, затушеваны многими осложняющими факторами. Необходимо было сначала выявить и изучить закономерности случайных явлений на более простом материале. Исторически таким материалом оказались азартные игры. Само слово «азарт» (франц. «le hasard») означает «случай». Схемы азартных игр дают исключительные по простоте и прозрачности модели случайных явлений. Поэтому и поныне примеры из области азартных игр широко используются при изучении теории вероятностей как упрощенные модели случайных явлений. Такие примеры в наиболее простом и наглядном виде иллюстрируют основные законы и правила теории вероятностей (скажем, табл. 7.1).

Дата добавления: 2014-11-18