Определение приведенного момента инерции механизма

Для звена, совершающего поступательное движение (ползун), кинетическая энергия

(3.30)

где m – масса звена, кг;

– скорость поступательно движущегося звена,

Для звена, совершающего вращательное движение (кривошип, коромысло), кинетическая энергия

(3.31)

где I – момент инерции относительно оси вращения, ;

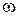– угловая скорость звена, с^-1.

Кинетическая энергия звена, совершающего сложное плоскопараллельное движение (шатун, тяга), равна сумме кинетических энергий поступательного движения с центром масс и вращательного движения вокруг центра масс. Следовательно, кинетическая энергия определяется как

(3.32)

где 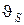– скорость центра масс звена, ;

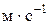I_S – момент инерции звена относительно оси, проходящей через центр масс, .

Складывая кинетические энергии всех звеньев, получим полную кинетическую энергию механизма.

Для данного механизма полная кинетическая энергия

(3.33)

или с учетом уравнений (3.30), (3.31) и (3.32)

В данном уравнении выражение в квадратных скобках представляет собой приведенный к начальному звену момент инерции механизма, т. е.

(3.34)

Кинетическая энергия звена приведения

(3.35)

Вычисляем приведенный момент инерции для 12-ти положений механизма и результаты расчета заносим в таблицу 3.2.

Для 1-го положения механизма приведенный момент инерции

По данным таблицы 3.2 строим диаграмму приведенного момента инерции механизма в функции угла поворота начального звена. При этом ось приведенного момента инерции расположим горизонтально.

Принимаем масштабный коэффициент , равный отношению величины максимального значения приведенного момента инерции к длине отрезка h, изображающего ее на диаграмме:

(3.36)

Таблица 3.2 – Результаты расчета приведенного момента инерции механизма, кг 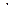м²

Номер положения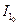
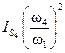
	0,01	0,00153	0,00405			0,009	0,00361	0,02821
	0,01	0,00116	0,00562	0,00141	0,00041	0,0084	0,00356	0,03057
	0,01	0,00041	0,00841	0,00356	0,00116	0,0056	0,00141	0,03057
	0,01		0,00901	0,00361	0,00153	0,0041		0,02821
	0,01	0,00041	0,00699	0,00194	0,00116	0,0056	0,00141	0,02753
	0,01	0,00116	0,00484	0,00049	0,00041	0,0084	0,00356	0,02888
	0,01	0,00153	0,00405			0,009	0,00361	0,02821
	0,01	0,00114	0,00484	0,00049	0,00041	0,007	0,00194	0,02582
	0,01	0,00041	0,00699	0,00194	0,00116	0,0048	0,00049	0,02583
	0,01		0,00901	0,00361	0,00153	0,0041		0,02821
	0,01	0,00041	0,00841	0,00356	0,00116	0,0048	0,00049	0,02888
	0,01	0,00116	0,00562	0,00141	0,00041	0,007	0,00194	0,02753

Для нашего случая масштабный коэффициент

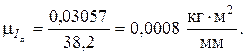
Методом исключения общего параметра 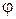из диаграмм и строим диаграмму энергомасс .

По данному коэффициенту неравномерности движения и средней угловой скорости 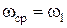определяем углы и 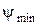, образуемые касательными к диаграмме энергомасс с осью абсцисс, по следующим зависимостям:

(3.37)

(3.38)

Подставляя числовые значения, получим:

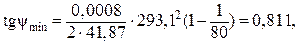
или

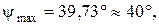
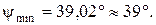
Построив стороны этих углов и перенеся их параллельно самим себе до касания с кривой энергомасс соответственно сверху и снизу, получим на оси отрезок , заключенный между этими касательными.

По отрезку определяем момент инерции маховика

(3.39)

Подставив числовые значения, получим:

Обычно маховик имеет форму либо колеса с массивным ободом (изготавливается из чугуна), соединенным со ступицей с помощью спиц, либо форму сплошного диска (изготавливается из стали).

Диаметр маховика с тяжелым ободом может быть определен по формуле:

(3.40)

где 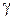– удельный вес материала маховика

(для чугуна );

– соответственно отношение ширины b и

высоты h обода к диаметру маховика (из конструктивных

соображений принимают: и ).

Диаметр маховика, выполненного в виде сплошного диска, определяется по формуле:

(3.41)

Выбираем конструкцию маховика в виде колеса с тяжелым ободом, для которого принимаем и . Тогда

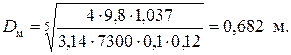
Принимаем диаметр маховика

Для чугунных маховиков необходимо, чтобы окружная скорость на ободе не превышала 30

В нашем случае

что превышает критическое значение.

Поэтому принимаем конструкцию стального маховика в виде сплошного диска.

Его диаметр определим по формуле (3.41), приняв для стали :

Принимаем диаметр маховика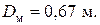

Так как маховый момент стального маховика в виде сплошного диска равен

(3.42)

то его массу определим по зависимости:

(3.43)

Толщина диска определяется как

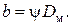(3.44)

Подставив числовые значения в уравнения (3.42), (3.43) и (3.44), получим параметры маховика:

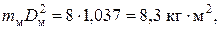
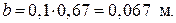
Выводы

Полученные величины значений диаметра 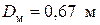и массы показывают, что такой маховик вполне может быть установлен на вал О данного механизма, чтобы обеспечить его вращение с заданным коэффициентом неравномерности

Дата добавления: 2014-11-18