Ідентифікація часових рядів

Структуру часового ряду в деяких випадках можна визначити графічно. Це стосується, наприклад, таких компонент ряду, як тренд і сезонні коливання. Однак чисту випадковість інколи помилково сприймають як наявність певної структури, і, навпаки, за шумом можна не розгледіти існування структури. Тому потрібні методи або інструменти, за допомогою яких можна було б звести нанівець ефект впливу шуму, після чого з’ясувати характеристики ряду, необхідні для побудови відповідної прогнозової моделі. Як правило, спочатку з’ясовують, із яким процесом доведеться працювати — стаціонарним чи нестаціонарним. Для будь-якого нестаціонарного ряду важливо визначити ознаку його нестаціонарності: чи описується він детермінованим трендом, чи є інтегрованим процесом і описується стохастичним трендом (лінійним або нелінійним), визначити наявність періодичної складової.

Перевірка стаціонарності часового ряду. Стаціонарні часові ряди передбачають, що процес породження наявних даних є лінійним. Вони не мають тренду або періодичної зміни середнього та дисперсії.

Перевірку гіпотез стосовно сталості середнього значення та дисперсії часового ряду можна здійснити кількома способами. Найпростішими з них є перевірка значущої відмінності двох серед­ніх значень для деяких підмножин вибірки (наприклад, для першої та останньої третин усього обсягу даних) за 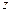— критерієм (критерій перевірки гіпотези про рівність середніх двох нормально розподілених вибірок) і для дисперсії, якщо справедливе припущення про нормальний розподіл, можна використати F-критерій. Розглянемо два поширені методи: метод перевірки різниць середніх рівнів і метод Форстера-Стьюарта.

Метод перевірки різниць середніх рівнів. Реалізація цього методу передбачає такі чотири кроки.

Крок перший. Вхідний часовий ряд 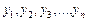розподіляють на дві приблизно однакові за кількістю спостережень частини: в першій частині п ₁ першої половини рівнів вхідного ряду, у другій — решта рівнів п ₂ ().

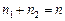Крок другий. Для кожної з цих частин розраховують середні значення й дисперсії: ; ; ; .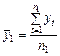

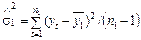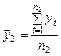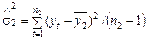Крок третій. Перевірка рівності (однорідності) дисперсій обох частин ряду за допомогою F- критерію, що порівнює розрахункове значення цього критерію:

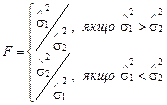(1.3.1)

із табличним (критичним) значенням критерію Фішера F _α із заданим рівнем значущості α. Якщо розрахункове значення F менше за табличне F _α, то гіпотезу про рівність дисперсій приймають, і можна переходити до четвертого кроку. Якщо F більше або дорів­нює F _α, гіпотезу про рівність дисперсій відхиляють і доходять висновку, що цей метод не дає відповіді щодо наявності тренду.

На четвертому кроці перевіряють гіпотезу про відсутність тренду за допомогою t -критерію Стьюдента.Для цього визначають розрахункове значення критерію Стьюдента за формулою:

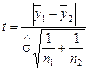, (1.3.2)

де 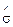— оцінка середньоквадратичного відхилення різниць середніх:

.

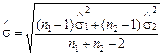Якщо розрахункове значення t менше за табличне t _α, то нульову гіпотезу не відхиляють, тобто тренд відсутній, інакше — тренд є. Зазначимо, що в цьому разі табличне значення t _αприймають для числа ступенів вільності, яке дорівнює 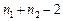, до того ж цей метод застосовують суто для рядів із монотонною тенденцією. Недолік методу полягає у неможливості правильно визначити існування тренду в тому разі, коли часовий ряд містить точку зміни тенденції у середині ряду.

Метод Форстера-Стьюарта. Цей метод має більші можливос­ті та дає надійніші результати, ніж попередній. Окрім тренду са-
мого ряду (тренду в середньому), він дає змогу встановити існування тренду дисперсії часового ряду: якщо тренду дисперсії
немає, то розкид рівнів ряду постійний; якщо дисперсія збільшується, то ряд «розхитується». Реалізація методу передбачає чотири кроки.

Крок перший. Порівнюють кожен рівень вхідного часового ряду, починаючи з другого рівня, з усіма попередніми, при цьому визначають дві числові послідовності:

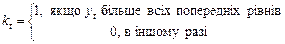(1.3.3)

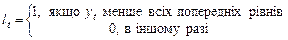(1.3.4)

t = 2, 3, …, n.

Крок другий. Розраховують величини с і d:

; (1.3.5)

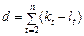. (1.3.6)

Величина c, яка характеризує зміну рівнів часового ряду, набуває значення від 0 (усі рівні ряду однакові) до п – 1 (ряд монотонний). Величина d характеризує зміну дисперсії часового ряду та змінюється від [–(п – 1)] — ряд поступово згасає, до (п – 1) — ряд поступово розхитується.

Крок т ретій Перевіряється гіпотеза стосовно того, чи можна вважати випадковими: 1) відхилення величини c від математичного сподівання ряду, в якому рівні розташовані випадково, 2) відхи­лення величини d від нуля. Цю перевірку здійснюють на підставі обчислення t -відношення відповідно для середньої та для дисперсії:

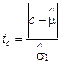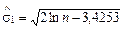; ; (1.3.7)

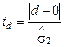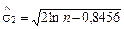; , (1.3.8)

де 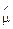— оцінка математичного сподівання ряду; 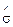₁ — оцінка середньоквадратичного відхилення для величини c; 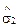— оцінка середньоквадратичного відхилення для величини d.

Таблиця 1.3.2

п
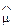
	3,858	5,195	5,990	6,557
1	1,288	1,677	1,882	2,019
2	1,964	2,279	2,447	2,561

Фрагмент розрахованих значень величин , 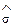₁ і 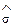₂ для різних п наведено в табл. 1.3.2 [25].

Крок четвертий. Розрахункові значення t_с i t_d порівнюють із табличним значенням t -критерію із заданим рівнем значущості t_α. Якщо розрахункове значення t менше за табличне t _α, то гіпотезу про відсутність відповідного тренду приймають, в іншому разі тренд існує. Наприклад, якщо t_с більше табличного значення t _α, a t_d менше t _α, то для заданого часового ряду існує тренд у серед­ньому, а тренду дисперсії рівнів ряду немає.

Тест Діккі-Фуллера призначений для того, щоб розрізняти часові ряди типу TS та DS. Відповідно нульовій гіпотезі 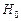досліджуваний ряд належить до типу DS. За альтернативною гіпотезою він може бути типу TS, але одночасно бути або нестаціонарним — мати детермінований тренд, або не мати тренду — бути стаціонарним. Виділяють простий тест Діккі-Фуллера — DF -тест — та розширений тест Діккі-Фуллера — АDF -тест. Розглянемо їх по порядку.

Простий DF-тест. Припустімо, що 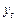може бути описано моделлю:

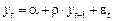, (1.3.9)

де випадкова величина є «білим шумом». Зазначимо, що модель (1.3.9) увібрала в себе риси як DS, так і TS процесів. Якщ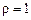о , то 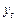— це випадкове блукання із дрейфом 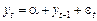, тобто є нестаціонарним DS процесом. Якщо 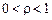, тоді маємо справу зі стаціонарним марківським процесом. Зазначимо, що 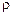не набуває значень, більших за 1, оскільки це передбачає вибуховий процес. Оскільки такі ряди мало імовірні в економічних дослідженнях, ми їх далі не розглядатимемо. Гіпотези щодо характеру ряду можна записати таким чином:

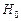: ряд є DS, якщо .

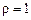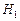: ряд є TS, якщо .

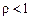У класичній лінійній регресії для перевірки такої гіпотези використовують односторонню t -статистику. Для зведення процедури перевірки нульової гіпотези до більш звичної (коли коефіцієнт за 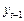дорівнює нулю) віднімемо з обох частин (1.3.9) 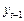. У результаті отримаємо регресію:

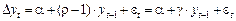, (1.3.10)

в якій перевіряємо наступну нульову гіпотезу проти альтернативної:

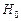: ряд є DS, якщо ,

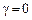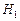: ряд є TS, якщо .

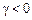Для звичайної регресії відношення 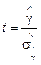порівнюється із критичним значенням t -розподілу. Однак у разі виконання гіпотези 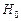, ряд 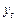є випадковим блуканням, його дисперсія прагне до нескінченності при збільшенні часу, і розподіл t -відношення не підпорядковується t -розподілу, а підпорядковується розподілу Діккі-Фуллера (DF), який, на відміну від 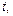позначається 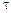. Тест, який використовує для перевірки типу нестаціонарності цей розподіл, за умови 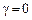, тобто коли процес належить типу DS, називають тестом Діккі-Фуллера.

Точна форма критерію значущості Діккі-Фуллера залежить від специфікації моделі, що підлягає тестуванню. Тому в загальному випадку розглядається модель:

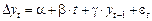, (1.3.11)

для якої можливі такі три випадки перевірки нульової гіпотези і три критичні величини DF -розподілу, розраховані в таблицях МакКіннона [29]:

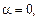
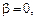
1) Модель без лінійного тренду та дрейфу ( 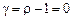). Для цього розподілу критичне значення DF позначимо . Нульова гіпотеза означає, що 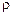= 1 і ряд 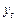— це випад­кове блукання без дрейфу, тобто є нестаціонарним (інтегрованим) процесом: .

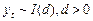Дата добавления: 2014-11-08